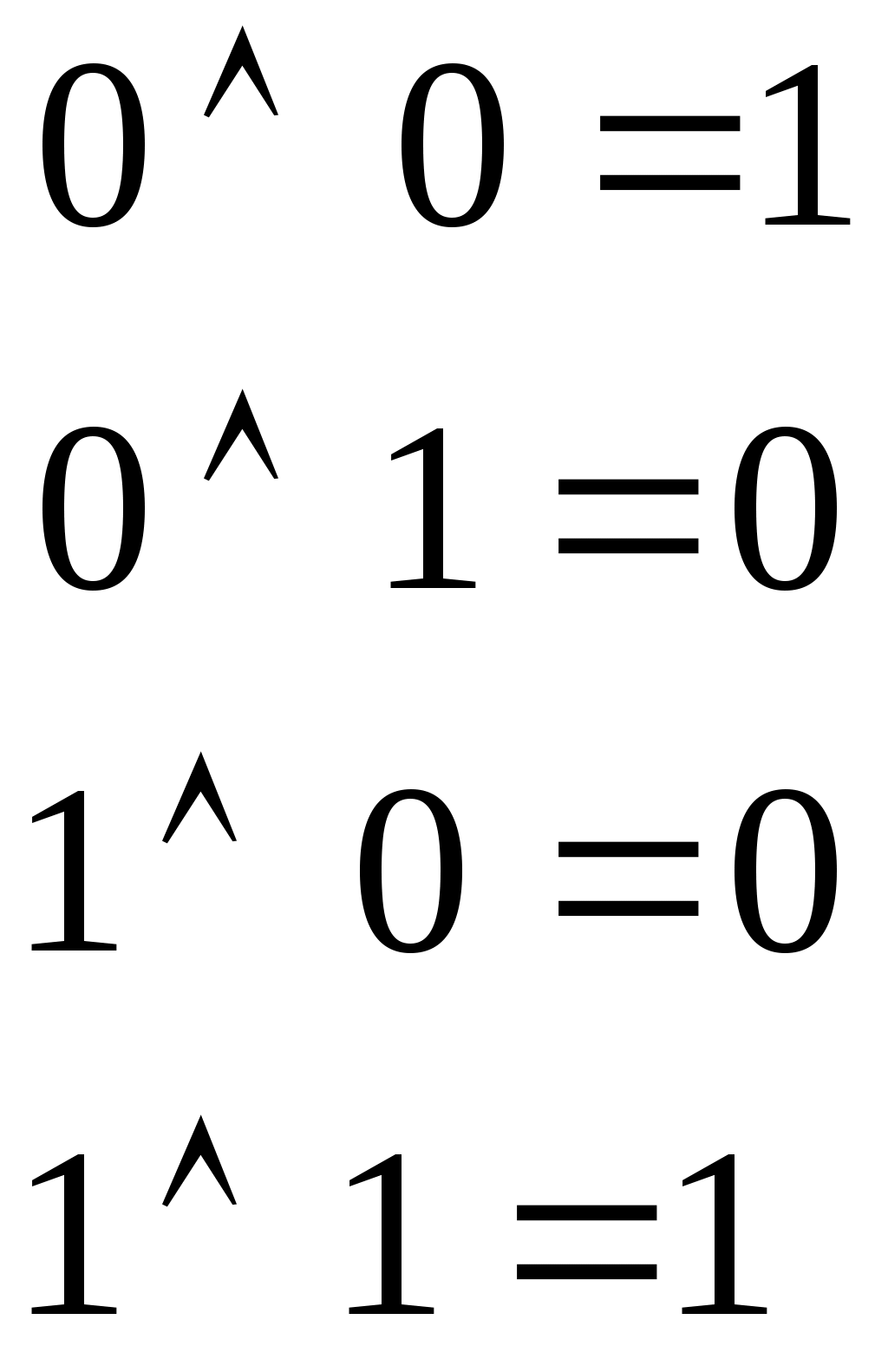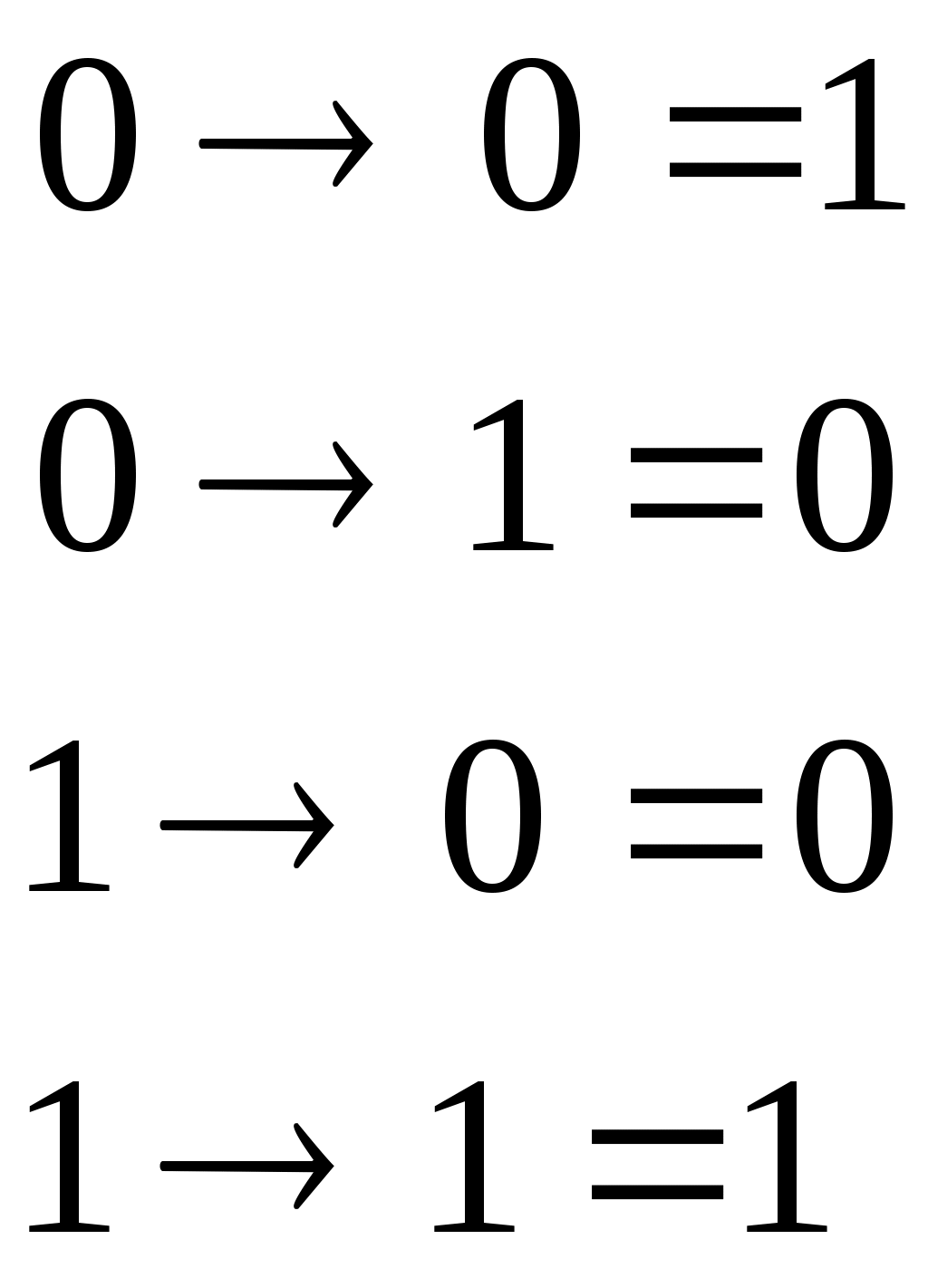5-СхЗерт. 1 3 лабораториялы жмыс. Саба таырыбы Логиканы негізгі ымдары Саба масаты
 Скачать 1.88 Mb.
|
B күрделі айтылымының ақиқаттық мәндері А және В айтылымдарына тепе-теңдік операциясын қолдану арқылы табылады да төмендегі кестемен анықталады:№ 1- 3 лабораториялық жұмыс. Сабақ тақырыбы: Логиканың негізгі ұғымдары Сабақ мақсаты: Математикалық логика жалпы логикалық математиканың қажеттілігіне лайықталған бөлігі. Ұзақ уақыт математикалық логика тек математикалық дәлелдеулерді зерттейтін теориялық ғылым саласы болды. Программамен басқарылатын есептеу машиналарының пайда болуына қарай математикалық логика қолданбалы сипатқа ие болды. Информациялық-логиканың есептерін шығаруда математикалық логиканың логика алгебрасы деп аталатын саласы жиі пайдаланылады. Бұл сала ЭЕМ-нің теориясына және басқа дискретті автоматтарға қолданылады. Жұмысты орындауға арналған әдістемелік нұсқау: Күрделі айтылымдар және логикалық байланыстармен қатар оларға қолданылатын негізгі логикалық операцияларды анықтайық. 1. Теріске шығару. А айтылымын теріске шығару  символымен белгіленеді де “А емес” деп оқылады. Айтылымның ақиқаттық мәндерінің теріске шығару ақиқаттық мәндері теріске шығару операциясымен айқындалады: 2. Конъюнкция. Екі айтылымның конъюнкциясы А  В деп белгіленеді.“А және В” деп оқылады. А 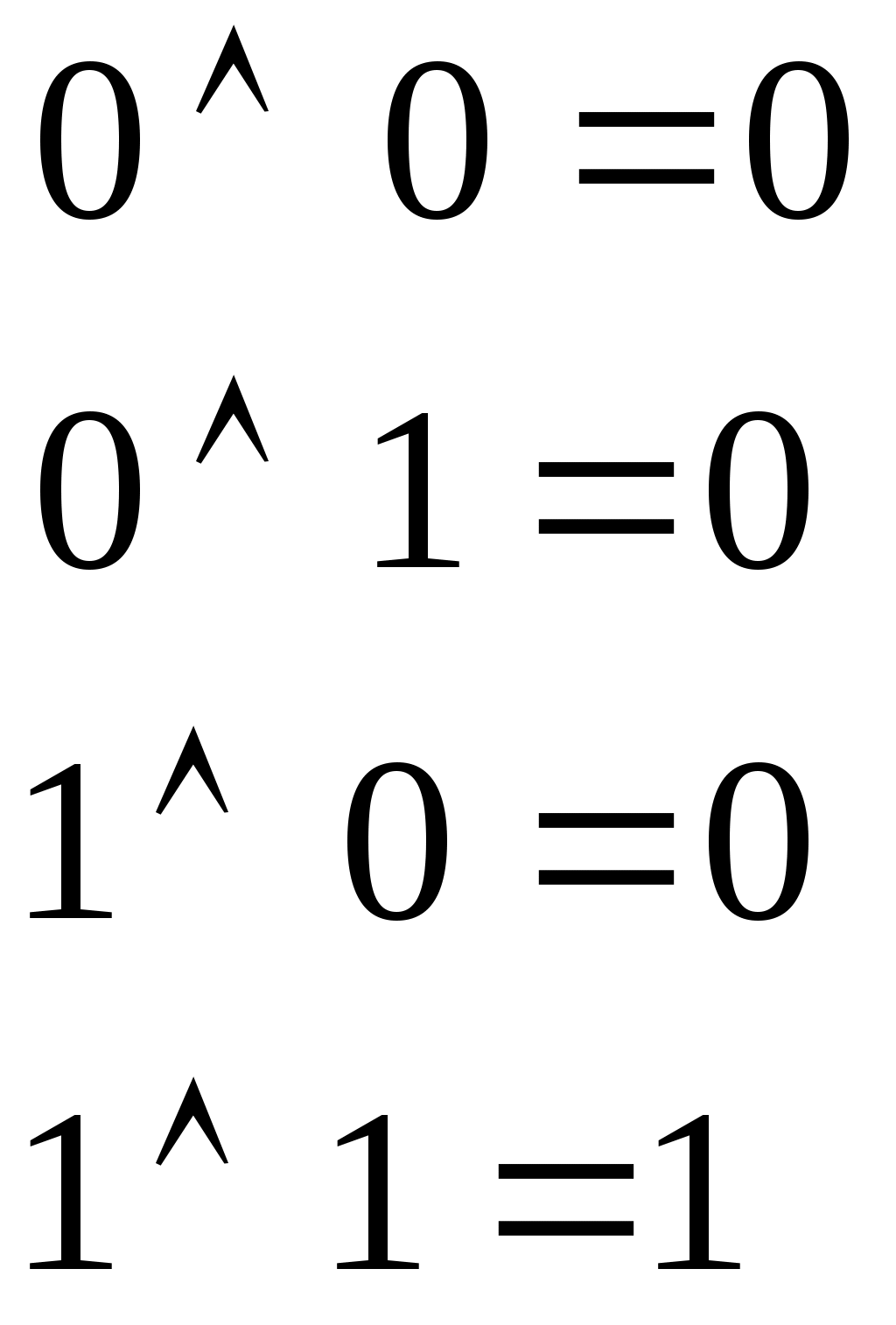В конъюнкциясының ақиқаттық мәндері А және В айтылымдарын логикалық көбейту арқылы есептелініп келесі кесте бойынша анықталады. 3. Екі айтылымның дизъюнкциясы АVВ таңбаларымен белгіленеді де “А немесе В” деп оқылады. А және В айтылымдарының ақиқаттық мәндеріне логикалық қосу АVВ операциясын қолданғандағы екі айтылымның логикалық қосындысының (дизъюнкциясы) ақиқаттық мәндері келесі кестеден анықталады. 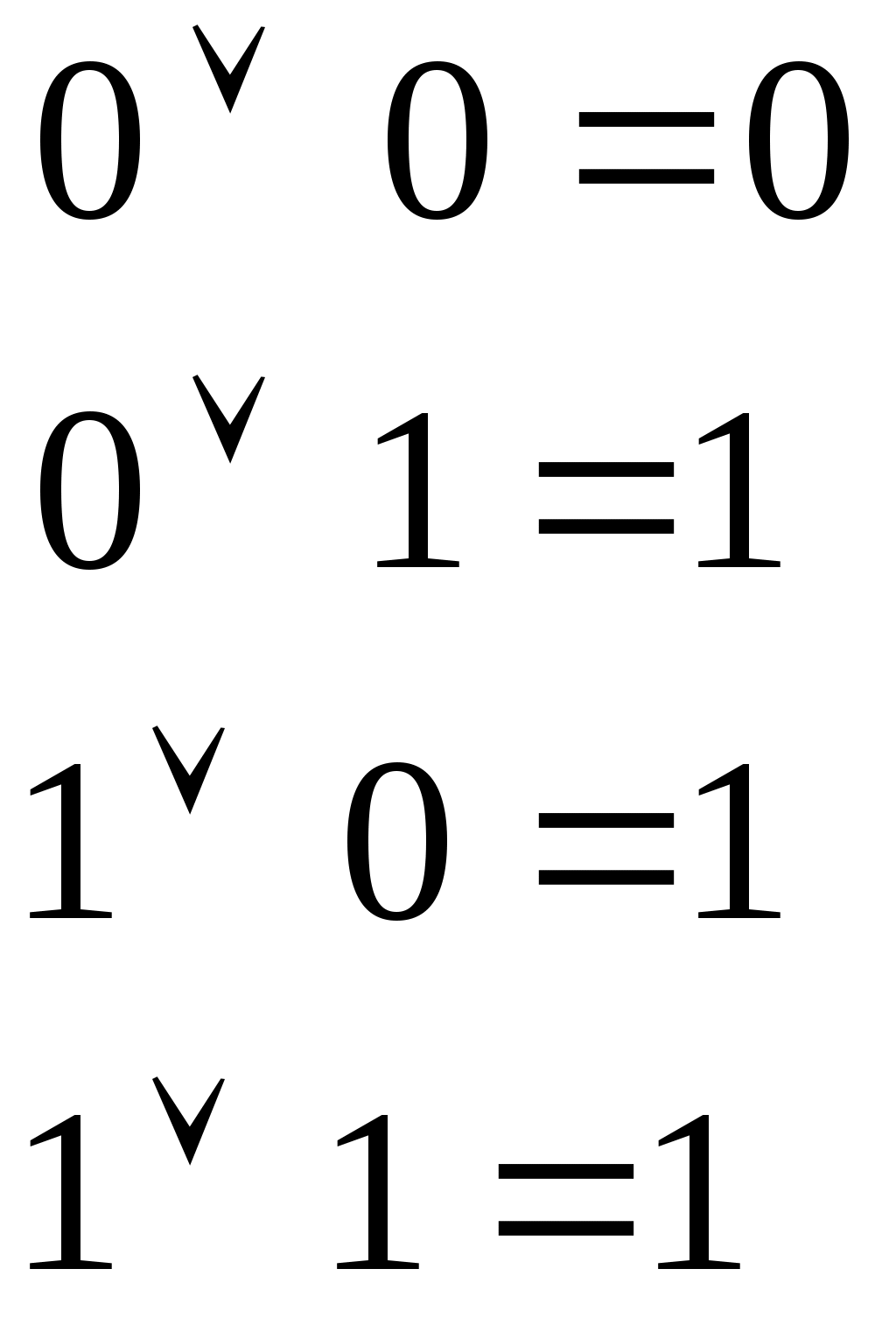 4. Тең мәнділік (тепе-теңділік). А және В айтылымдарының тепе-теңділігі A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В) болып белгіленеді де “А В-ға тепе-тең” деп оқылады. A
символдарымен белгіленеді және “егер А онда В” деп оқылады. Ақиқаттық мәндері кестеден анықталады.
1) да, ал бірлікті нөл теріске шығарады (
0). 1-суретте «Емес» логикалық элементін транзистордың көмегімен орындау схемасы келтірілген. 
; 19. 
; 20.
21. 
23. 
Орындалу реті: | А | В |  В |  |  |  |  |  |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| Теңдіктің сол жағы | Теңдіктің оң жағы | ||||||
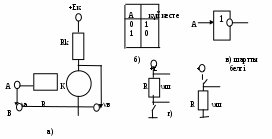
1-24 формулалардан кез келген логикалық байланыстарды негізгі үш байланыс арқылы (терістер, дизъюнкция, конъюкция) өрнектеуге болатынын байқаймыз. Ал ол үш байланыс шеффер байланыс арқылы өрнектеледі.
Мәндес формулалар Нормальді формалар
Логикалық өрнекті түрлендіріп нормальді форма деп аталатын түрлердің біріне келтіргенде оның құрылымы көрнекі, айқын болады. Логикалық өрнектердің екі түрлі нормальді формасы бар.
Оның біріншісі - конъюктивтік нормальді форма (КНФ) дизъюнкциялардың конъюкциясы болып табылады және де оның әрбір дизъюнкциясының жеке мүшелері негізгі айтылымдар немесе олардың терістері болады.
Екіншісі – дизъюнктивтік нормальді форма (ДНФ) – конъюкциялардың дизъюнкциясынан құрылатын және әрбір конъюкциясының жеке мүшелері негізгі айтылым немесе олардың терістері болатын өрнек.
Логикалық өрнектерді нормальді формаға түрлендіру үшін қолданылатын нұсқаулар:
а) және таңбаларын алгебрада *, + амалдарын пайдаланғанға сәйкес қолдану керек (ауыстырымдылық, үлестірімділік, т.б.). ( 2, 7, 8, 13, 16, 17 формулалар).
б) Екі еселі (жұп еселі) терістеу орнына негізгі өрнекті қалдыруға болады.
в) Екі айтылымның конъюкциясының терістерін олардың терістеулерінің дизъюнкциясымен, ал екі айтылымның дизъюнкциясының терістеуін олардың терістеулерінің конъюкциясынан ауыстыруға болады (14, 15 формулалар).
г) АВ, АВ, АВ, АВ өрнектерін 20- 23 формулаларын пайдаланып түрлендіреміз.
Бұл ережелерді пайдалану реті:
1) ережесін қолданып тең мәнділік импликация және үйлесімсіздік (шефер операциясы) байланыстарын жоямыз.
2) ережесін қолданып терістеу операциясы бар жақшаларды түрлендіріп, жеке айтылымдардың терістеуі болатындай етіп жазамыз.
3) Соңында а) және б) ережелерінің көмегімен өрнектер ажыратылып, екі еселі терістеу операциялары алынып тасталады.
Күрделі айтылымдардың ақиқаттық мәндерінің тұрақты ақиқат немесе тұрақты жалған болуы мынадай үш ерженің көмегімен анықталады:
1) АА әркез ақиқат. 2) Егер А ақиқат болса, ал В кез келген айтылым болса, онда АВ ақиқат.
3) Егер А және В ақиқат болса, онда АВ ақиқат болады.
Бірнеше айтылымнан құрылған логикалық өрнектердің тепе-теңдігін дәлелдеу 20-шы формулны дәлелдеген жолмен анықталады. Мысал: (А → С) ( С →
) логикалық өрнегін ДНФ және КНФ формаларына түрлендіру керек. Алынған формуланы ақиқаттық кестесі арқылы тексеруге болады. Шығарылуы жоғарыдағы формулалар мен ережелерді аайдаланып:(А →С) (С→
) ( С) (
) [( C) ( )][( C) ( )]=[( С) ( )][( )( )]=[( С) (CB)] [(A )( )]=( С)CB) (A )=[ C (1B)] [ (AB) ]=( С)1) ( 1 )=( С) ( )=( C) ( ) КНФ алдық. Енді КНФ-тен ДНФ-ке түрлендірейік.(
C) ( )=( )( )( )(C )=ДНФ формуладағы жақшаны алып тастауға болады. Енді теңдікті тексереміз:
(AC)(CB)=(
C) ( )=( )( )( C)1 кесте: (А → С) (C
)| А | В | С | А → С | | С → | (А → С) (C ) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
2 кесте: (AC) (
) | А | В | С | | | | AC | | (AC) ( ) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
3 кесте: (
)( )( C)| А | В | С | | | | | | C | ( )( )( C) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1, 2 және 3 кестедегі соңғы бағандарының мәндері бірдей болғандықтан теңдіктердің тепетеңдіктері дәлелденді.
Тапсырмалар:
Берілген логикалық өрнектерді конъюкция және дизъюнкция нормальді формулаларға түрлендіру керек.
| Нұсқа | Логикалық өрнек | Нұсқа | Логикалық өрнек |
| 1 | ( C) ( /В) | 9 | (А )/(СВ) |
| 2 | (АC) (В/С) | 10 | ( )/( В) |
| 3 | ( )(СВ) | 11 | ( В) (В ) |
| 4 | (СА) ( С) | 12 | (АВ) ( С) |
| 5 | (А/В) (В ) | 13 | ( ) ( С) |
| 6 | (В/ )( С) | 14 | (АВ) ( / ) |
| 7 | ( /В) (ВС) | 15 | (АВ) ( / ) |
| 8 | ( / )( ) | 16 | |
Тапсырманың бағалануы:Осы лабораториялық жұмысты толық және қатесіз орындпғандар жалпы – 5 балмен бағаланады.
Пайдалынған әдебиеттер:
Н.В.Макарова, Е.Л.Рамин и др. Основы схемотехники: Сборник задач. Под. ред. Н.В.Макаровой.- М.: Финансы и статистика, 1997.
Информатика и программирование на ЭВМ. Алматы: КазГАСА, 1996
С.Мюллер. Ремонт и модерниаци ПК. Москва Санкт-Петербург. Киев 2004г.
В.С.Янпольский. Основы автоматики и вычислительной техники. Москва. «Просвещение» 1991 г.
Гришкун В.В. Организация компьютеризированного обучения на базе иерархических структур данных. – Алматы, 1996.
Акимов О.Е. Дискретная математика. – Комосмольск-на-Амуре, 1996.
№ 8- 11 лабораториялық жұмыс.