лекц инф копия. 1. Информатика как научная дисциплина. Понятие информации Информатика как научная
 Скачать 396.97 Kb. Скачать 396.97 Kb.
|
|
Звук представляет собой распространяющуюся в воздухе, воде или другой среде волну с непрерывно меняющейся интенсивностью и частотой. Человек воспринимает звуковые волны (колебания воздуха) с помощью слуха в форме звуков различной громкости и тона, чем больше интенсивность звуковой волны, тем громче, звук, чем больше частота волны, тем выше тон звука. Для того чтобы компьютер мог обрабатывать реальный (записанный) звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина интенсивности звука. Для записи аналогового звука и его преобразования в цифровую форму используется микрофон, подключенный к звуковой плате. Качество полученного цифрового звука зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее «лесенка» цифрового звукового сигнала повторяет кривую аналогового сигнала. Частота дискретизации звука — это количество измерений громкости звука за одну секунду. Частота дискретизации звука может лежать в диапазоне от 8 000 до 50 000 измерений громкости звука за одну секунду. Каждому уровню дискретизации присваивается определенное значение уровня громкости звука. Уровни громкости звука можно рассматривать как набор возможных состояний N, для кодирования которых необходимо определенное количество информации I, которое называется глубиной кодирования звука. Глубина кодирования звука — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука. Если известна глубина кодирования, то количество уровней громкости цифрового звука можно рассчитать по формуле N = 2I Пусть глубина кодирования звука составляет 16 битов, тогда количество уровней громкости звука равно N = 2I = 216 = 65 536. Чем больше частота дискретизации и глубина кодирования звука, тем более качественным будет звучание оцифрованного звука. Самое низкое качество оцифрованного звука, соответствующее качеству телефонной связи, будет при частоте дискретизации 8000 раз в секунду, глубине кодирования 8 битов и записи одной звуковой дорожки (режим моно). Высокое качество оцифрованного звука, соответствующее качеству аудио-CD, обеспечивается при частоте дискретизации 48 000 раз в секунду, глубине кодирования 16 битов и записи двух звуковых дорожек (режим стерео). Дискретное (цифровое) представление видеоинформации В последнее время компьютер все чаще используется для работы с видеоинформацией. Простейшей такой работой является просмотр кинофильмов и видеоклипов. Что представляет собой фильм с точки зрения информатики? Прежде всего, это сочетание звуковой и графической информации. Кроме того, для создания на экране эффекта движения используется дискретная технология быстрой смены статических картинок. Исследования показали, что если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные. При использовании традиционных методов сохранения информации электронная версия фильма получается слишком большой. Способ уменьшения объема видео: первый кадр запоминается целиком (ключевой), а в следующих сохраняются только отличия от начального кадра (разностные кадры). 16. Основные логические операции Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0». Из этого следует, что одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных. Логика – это наука о формах и способах мышления. Основы формальной логики заложил древнегреческий мыслитель Аристотель. Логические переменные в алгебре логики обозначаются прописными латинскими буквами, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0). Логическое умножение (конъюнкция) «И» AB ABистинно тогда и только тогда, когда оба высказывания Aи B истинны. Логическое сложение (дизъюнкция) «ИЛИ» AB ABложно тогда и только тогда, когда оба высказывания A и Bложны. Логическое отрицание (инверсия) «НЕ» A, ( 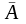 ) )Логическое отрицание (инверсия) делает истинное выражение ложным и, наоборот, ложное – истинным. Таблица истинности для основных логических функций
17. Логические элементы ЭВМ Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логический элемент – простейшая структурная единицаЭВМ – выполняющая определенную логическую операцию над двоичными переменными согласно правилам алгебры логики. Реализуется обычно на электронных приборах (полупроводниковых диодах, транзисторах) и резисторах, либо в виде интегральной микросхемы; имеет несколько входов для приема сигналов, соответствующих исходным переменным, и выход для выдачи сигнала, соответствующего результату операций. Для логических элементов приняты дискретные значения входных и выходных сигналов («0» и «1»). Базовые логические элементы ЭВМ реализуют три основные логические операции: конъюнктор – логический элемент «И» логическое умножение; дизъюнктор – логический элемент «ИЛИ» логическое сложение; инвертор – логический элемент «НЕ» инверсию. Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков». Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции. Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции. Конъюнктор Конъюнкция – соответствует союзу «И», обозначается знаком , иначе называется логическим умножением. Конъюнкция двух логических переменных истинна тогда и только тогда, когда обе переменные истинны. Т  аблица истинности аблица истинностифункции логического умножения:
Конъюнктор (логический элемент «И») – реализует операцию конъюнкции. На входы А и В логического элемента «И» подаются два сигнала (00, 01, 10, 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения. Дизъюнктор Дизъюнкция – соответствует союзу «ИЛИ», обозначается знаком , иначе называется логическим сложением. Дизъюнкция двух логических переменных истинна тогда, когда истинна хотя бы одна переменная. Т  аблица истинности аблица истинностифункции логического сложения:
Дизъюнктор (логический элемент «ИЛИ») – реализует операцию дизъюнкции. На входы А и В логического элемента «ИЛИ» подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения. Инвертор – логический элемент «НЕ» Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания или инверсией. Логическое отрицание (инверсия) делает истинное выражение ложным и, наоборот, ложное – истинным. Операцию логического отрицания (инверсию) над логическим высказыванием A в алгебре логики принято обозначать A. Т  аблица истинности аблица истинностифункции логического отрицания:
Инвертор – реализует операцию отрицания, или инверсию. На вход А логического элемента подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии. Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов. 18. Алгоритмы и свойства алгоритмов Современный компьютер способен действовать только по формальным схемам, заготовленным для него человеком. Поэтому, чтобы привлечь компьютер к исследованию объекта, процесса, явления или к “рутинной” обработке информации, прежде всего надо: четко поставить задачу (разработать модель), определить исходные данные, форму представления результатов. далее необходимо создать алгоритм решения задачи и программу, которая будет понята компьютером. Возникает классическая для информатики триада: модель — алгоритм — программа Во многих случаях этапы моделирования и алгоритмизации неотделимы друг от друга (например, при разработке модели производственного процесса). Слово «алгоритм» произошло от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми, описавшего в IX веке правила выполнения вычислений с многозначными десятичными числами. Правила сложения, вычитания, умножения столбиком, деления «уголком», которые мы учим в младших классах, - это алгоритмы аль-Хорезми. Для составления программы, предназначенной для решения на ЭВМ какой-либо задачи, требуется составление алгоритма ее решения — точного предписания, которое определяет процесс, ведущий от исходных данных к требуемому конечному результату. Работа по решению задач с использованием компьютера делится на несколько этапов. Основными этапами при этом является формализация и алгоритмизация решаемой задачи. На этапе формализации задача переводится на язык математических формул, уравнений, отношений. После формализации описывается алгоритм решения задачи. Алгоритм является одним из фундаментальных понятий в информатике. Алгоритм – последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд. Исполнителем алгоритма может быть человек или автоматическое устройство – компьютеры, роботы, станки, спутники, сложная бытовая техника и даже детские игрушки. Каждый алгоритм создается в расчете на вполне конкретного исполнителя. Применительно к компьютерам алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение результатов. Термин вычислительный процесс распространяется на обработку не только числовой информации, но и других видов информации (символьной, графической или звуковой). Действия, которые может совершать исполнитель, называют системой команд исполнителя. Алгоритм должен содержать только те действия, которые допустимы для данного исполнителя. Свойства алгоритмов: дискретность – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов; детерминированность – исполнитель должен выполнять команды алгоритма в строго определенной последовательности, каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего; однозначность – каждая команда определяет однозначное действие исполнителя; понятность – понимание исполнителем команд, в алгоритме используются только команды из системы команд исполнителя; результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов; массовость – один и тот же алгоритм может применяться к большому количеству однотипных задач. Способы описания алгоритмов Типовые конструкции алгоритмов: линейная– описание действий, которые выполняются однократно в заданном порядке; циклическая – описание действий или группы действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. разветвляющаяся – алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий; вспомогательная – алгоритм, который можно использовать в других алгоритмах, указав только его имя. Форма и способ записи алгоритма зависит от того, кто будет исполнителем. Представление алгоритмов можно разделить на две группы: естественное: словесный способ (алгоритм записан на естественном языке); графический способ (алгоритм изображен в виде блок-схемы); формальное. Естественное представление алгоритма Словесный способ: При словесном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий. Графический способ (блок-схемы): Блок-схема позволяет сделать алгоритм более наглядным и выделяет в алгоритме основные алгоритмические структуры (линейная, ветвление, выбор и цикл). Элементы алгоритмы изображаются на блок-схеме с помощью различных геометрических фигур. Элементы алгоритма соединены стрелками, указывающими шаги выполнения алгоритма. Элементы блок-схем
Формальное представление алгоритмов Формальное представление алгоритмов – это способ записи алгоритмов с использованием алгоритмических языков, либо языков программирования. |