1. Структура потерь электроэнергии в электрических сетях. Технические потери электроэнергии
 Скачать 142.31 Kb. Скачать 142.31 Kb.
|
2.2 Методы расчета потерь электроэнергии в распределительных сетях 0,38-6-10 кВСети 0,38 - 6 - 10 кВ энергосистем характеризуются относительной простотой схемы каждой линии, большим количеством таких линий и низкой достоверностью информации о нагрузках трансформаторов. Перечисленные факторы делают нецелесообразным на данном этапе применение для расчетов потерь электроэнергии в этих сетях методов, аналогичных применяемым в сетях более высоких напряжений и основанных на наличии информации о каждом элементе сети. В связи с этим получили распространение методы, основанные на представлении линий 0,38-6-10 кВ в виде эквивалентных сопротивлений [3]. Нагрузочные потери электроэнергии в линии определяют по одной из двух формул в зависимости от того, какая информация о нагрузке головного участка имеется - активная WРи реактивная wQ энергия, переданная за время Т или максимальная токовая нагрузка Imax:  , (2.8) , (2.8)Или 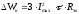 , (2.9) , (2.9)где kфР и kфQ - коэффициенты формы графиков активной и реактивной мощности; Uэк - эквивалентное напряжение сети, учитывающее изменение фактического напряжения как во времени, так и вдоль линии. Если графики Р и Qна головном участке не регистрируются, коэффициент формы графика рекомендуется определять по (2.7). Эквивалентное напряжение определяют по эмпирической формуле:  , (2.10) , (2.10)где U1, U2 - напряжения в ЦП в режимах наибольших и наименьших нагрузок; k1 = 0,9 для сетей 0,38-6-10 кВ. В этом случае формула (2.8) приобретает вид: 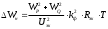 , (2.11) , (2.11)где kф2определяют по (2.7), исходя из данных о коэффициенте заполнения графика активной нагрузки. В связи с несовпадением времени замера токовой нагрузки с неизвестным временем ее действительного максимума формула (2.9) дает заниженные результаты. Устранение систематической погрешности достигается увеличением значения, получаемого по (2.9), в 1,37 раза. Расчетная формула приобретает вид: 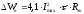 . (2.12) . (2.12)Эквивалентное сопротивление линий 0,38-6-10 кВ при неизвестных нагрузках элементов определяют исходя из допущения одинаковой относительной загрузки трансформаторов. В этом случае расчетная формула имеет вид:  , (2.13) , (2.13)где Sтi - суммарная номинальная мощность распределительных трансформаторов (РТ), получающих питание по i-му участку линий сопротивлением Rлi, п - число участков линий; Sтj - номинальная мощность i-го PТ сопротивлением Rтj; т - число РТ; Sт. г - суммарная мощность РТ, присоединенных к рассматриваемой линии. Расчет Rэкпо (2.13) предполагает обработку схемы каждой линии 0,38-6-10 кВ (нумерацию узлов, кодирование марок проводов и мощностей РТ и т.п.). Вследствие большого числа линий такой расчет Rэкможет быть затруднительным из-за больших трудозатрат. В этом случае используют регрессионные зависимости, позволяющие определять Rэк,исходя из обобщенных параметров линии: суммарной длины участков линии, сечения провода и длины магистрали, разветвлений и т.п. Для практического использования наиболее целесообразна зависимость: 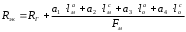 , (2.14) , (2.14)где RГ - сопротивление головного участка линии; lма, lмс - суммарные длины участков магистрали (без головного участка) с алюминиевыми и стальными проводами соответственно; lоа, lос - то же участков линии, относящихся к ответвлениям от магистрали; FM - сечение провода магистрали; а1 - а4 - табличные коэффициенты. В связи с этим зависимость (2.14) и последующее определение с ее помощью потерь электроэнергии в линии целесообразно использовать для решения двух задач: определения суммарных потерь в k линиях как суммы значений, рассчитанных по (2.11) или (2.12) для каждой линии (в этом случае погрешности уменьшаются приблизительно в √k раз); определения линий с повышенными потерями (очаги потерь). К таким линиям относят линии, для которых верхняя граница интервала неопределенности потерь превышает установленную норму (например, 5%). |
