games бак Мэ 12. 4 бескоалиционные(некооперативные) игры
 Скачать 238 Kb. Скачать 238 Kb.
|
|
1 NE: цена низкая | не входить,если цена низкая; входить, если высокая} Если монополия назначит низкую цену - стратегия конкурента содержит наилучший ответ ( 0 >(- 25)); если конкурентом выбрана стратегия "не входить,если цена низкая; входить, если высокая", то монополия, предвидя реакцию конкурента и выбирая между 43(цена низкая, он не входит) и 40(цена высокая - входит) , предпочитает назначить низкую цену. 2 NE: { цена высокая | входить всегда} Предположим, конкурент утверждает, что он войдет на рынок вне зависимости от того, какую цену назначит монополист. В этом случае монополист, выбирая между 38 и 40, должен назначить оставить цену на прежнем монопольно высоком уровне. Эта пара стратегий также будет являться равновесием по Нэшу(если входит- цена высокая, если цена высокая - входит): но его не следует рассматривать,т.к. оно основывается на incrediblethreats(необоснованных угрозах). Итак, игрок пытается убедить другого, что он будет придерживаться определенной стратегии, в случае тех или иных ходов со стороны партнера( даже если вы снизите цены - я все равно войду на рынок). Но эта угроза необоснованная , т.к. в случае снижения цен, конкурент не войдет на рынок( иначе вместо 0 он получит - минус 25) Необоснованные угрозы(incrediblethreats)- угрозы, которые не будут реализованы, коль скоро дело дойдет до конкретной ситуации, которую пытается предотвратить угрожающий. Не будут реализованы , т.к. это не в интересах самого игрока, угрожающего партнеру(это решение не является равновесным в усеченной игре) Такого рода угрозы следует игнорировать, отбрасывая соответствующие равновесия по Нэшу, как не являющиеся совершенными равновесиями по Нэшу(subgameperfectNashequilibrium - SPNE). Кстати, обратите внимание на следующие обстоятельства: • равновесный по Нэшу исход игры, найденный методом обратной индукции (aM*, RK(aM*))=(цена низкая; не входить) соответствет совершенному равновесию по Нэшу (SPNE) : {aM*, RK(aM)} ={цена низкая | не входить,если цена низкая; входить, если высокая}; • второе равновесие по Нэшу, отброшенное нами, основывается на использовании слабо доминируемой стратегии второго игрока( по этому поводу целесообразно обратиться к учебнику Creps, разделы 12.7.1-12.7.2, рр.417- 425). Пример 2. Бен предлагает Марии выйти за него замуж. Экстенсивная форма представления игры: 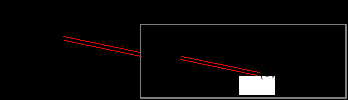 Равновесный по Нэшу исход этой игры (aM*, RB(aM*))=(Мария скажет нет, Вен найдет другую), где RB(aM*) - реакция Бена на оптимальное решение Марии: aM*). несложно найти, используя метод обратной индукции:  Однако, с тем, чтобы сформулировать стратегии Вена и выделить все равновесные сочетания стратегий игроков, удобнее перейти от экстенсивной к нормальной форме представления этой игры: Стратегии Марии: aM={ да , нет} Стратегии Бена: 1 - если да , то отлично, если "нет" - найду другую 2 - если да, то отлично, если нет - самоубийство
NE :
Как мы видим равновесный по Нэшу исход игры, найденный методом обратной индукции (aM*, RB(aM*))=(Мария скажет нет, Вен найдет другую) соответствет совершенному равновесию по Нэшу (SPNE) : (aM*, RB(aM))= {"нет"|если "да",то отлично; если "нет", найдет другую}. Результат рассмотрения этих двух примеров не случаен, поскольку в играх с совершенной информацией множество NE, выявленных методом обратной индукции всегда совпадает с множеством SPNE . Это происходит вследствие того, что в играх с совершенной информацией каждая неокончательная вершина является началом усечения игры, и последовательно выявляя методом обратной индукции оптимальные стратегии игроков в рамках каждого усечения игры, мы тем самым выявляем лишь совершенные равновесия по Нэшу. Совпадение множества NE, выявленных методом обратной индукции с множеством SPNE в сочетании с теоремой Zermelo( Zermelo'sTheorem)(формулировку теоремы см. выше), дает нам веское основание полагать что 1)любая конечная игра с совершенной информацией имеет совершенное равновесие по Нэшу (SPNE)в чистых стратегиях 2) это совершенное равновесие (SPNE) единственно, если игроки не имеют одинаковых выигрышей в различных окончательных позициях. Приложения: Равновесие по Штакельбергу. 2. 2. ИГРЫ С ПОЛНОЙ, НО НЕСОВЕРШЕННОЙ ИНФОРМАЦИЕЙ. ИНФОРМАЦИОННЫЕ МНОЖЕСТВА. УСЕЧЕНИЯ ИГРЫ В УСЛОВИЯХ НЕСОВЕРШЕНСТВА ИНФОРМАЦИИ. Если в задачах с совершенной информацией на каждой стадии решалась задача максимизации полезности одним из игроков(поочередно), то в условиях несовершенства информации речь идет о рассмотрении своего рода "одновременной" игры.( простейший пример : модель дуополии Курно). Def. Информационное множество(informationset): совокупность состояний(nodes), неразличимых для игрока(на дереве игры выделено пунктиром: игрок 2 не знает, как сыграл игрок 1). Игрок знает в каком именно информационном множестве он находится, но не знает в какой именно позиции данного множества.  При этом, все позиции из одного информационного множества должны иметь одно и тоже число альтернатив и никакая позиция не должна следовать за другой позицией из того же самого информационного множества. Кстати, игры с совершенной информацией иначе можно определить как игры, которых информационные множества состоят из одного элемента (asingletoninformationset). Def. "Усечение игры" или "усеченная игра"(subgame) Gs для игр с несовершенной информациейобладает следующими свойствами: - начинается в одной из неокончательных определенных позиций (a singleton information set); - начав играть в усечении игры(subgame), партнеры продожают делать это до конца игры; - все игроки знают, что они играют в данном усечении игры,что исключает возможность "broken" (т.е. дробных) информационных множеств как на приведенных ниже рисунках (непрерывной линией выделены информационные множества). Все группы, выделенные пунктиром не являются усечениями игры.   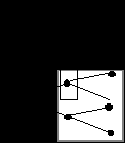 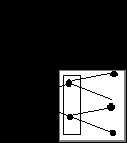 Пример:   Cтратегии первого игрока: • играть L играть R Cтратегии второго игрока: всегда выбиратьR ' всегда выбиратьL' • eсли первый игрок играет R, играть R ', eсли первый игрок играет L, играть L ' eсли первый игрок играет R, играть L ', eсли первый игрок играет L, играть R ' Cтратегии третьего игрока: всегда выбиратьR" всегда выбиратьL" • eсли (R, R ') играть R", в ином случае( не (R, R ')) выбиратьL" eсли (R, R ') играть L", в ином случае( не (R, R ')) выбиратьR" Равновесные стратегии: ( L; eсли R, то R ', eсли L, тоL ' ; eсли (R, R '),то R", в ином случае -L") Исход игры: ( L; L ' ; L") Обратите внимание на различие между равновесными стратегиями и исходом игры. В приведенной игре всего одно усечение игры, выделенное пунктирной линией( все варианты выделения информационных множеств, начинающихся в позициях 2-го игрока приходится отбросить, т.к. это приведет к разбиению информационных множеств(т.е."brokeninformationset"). Рассмотренная выше игра имеет тривиальное решение ввиду наличия у игроков 1 и 3 доминирующих стратегий. Изменим две цифры (они выделены),  Для того, чтобы в этих условиях попытаться предугадать исход этой игры с несовершенной информацией, следует располагать оценками вероятности того, что будет достигнута та или иная из позиций, входящих в информационное множество. Если не будут последовательно выбраны ходы (R, R'), то субъективная ожидаемая полезность, которую игрок 3 припишет выбору L" и R" в информационном множестве Eu3( L") =Р(L' L) (0) + Р(R' L)(6)+ Р(R)(4) Eu3( R") =Р(L' L) (3) + Р(R' L)(5)+ Р(R)(2) В частности, если игрок 3 полагает, что вероятность выбора стратегииL первым игроком , т.е. Р(L) равна a , а вероятность выбора стратегии L' вторым игроком в достигнутой позиции равна b, то вероятность Р(L'/ L) равна а b, вероятность Р(R'/ L) равна а (1- b), вероятность Р(L'/ R) равна (1- а) Например, при а=0.5; b=0.2 , третий игрок, оказавшись в информационном множестве, отдаст предпочтение стратегии L".
2.3. ИГРЫ С "ПОЧТИ СОВЕРШЕННОЙ ИНФОРМАЦИЕЙ".ПОВТОРЯЕМЫЕ ИГРЫ "Предположим, что игру можно разделить на ряд периодов t =1,2,..T(где Tконечно или бесконечно), что в каждый период tвремени игроки одновременно выбирают ходы, зная все ходы, выбранные всеми с периода 1 до периода t -1 . Из- за того, что такая игра предполагает одновременность только в рамках периода, мы называем эти расширенные формы играми с "почти совершенной" информацией. Простейшим примером такой игры является "повторяемая игра", в которой простая однопериодная игра с одновременным ходом повторяется Т раз и в момент t игроки знают все ходы произведенные до t. Однопериодная игра одновременного хода называется составной игрой " ( astagegame)(Тироль "Рынки и рыночная власть", с.674) 2.3.1. ИГРЫ С КОНЕЧНЫМ , ИЗВЕСТНЫМ ЧИСЛОМ ПОВТОРЕНИЙ( FINITELYREPEATEDGAMES). ПАРАДОКС СЕТИ МАГАЗИНОВ(THE CHAINSTORE PARADOX). Итак, рассмотрим динамическую игру, являющуюся многократным повторением игры, записанной в нормальном виде. Упрощающее предположение: в составной игре(stagegame) существует лишь одно равновесие по Нэшу. В этом случае именно оно и избирается в каждой повторяемой составной игре. При этом выигрыш в такого рода играх представляет собой приведенную к единому моменту сумму выигрышей, получаемых в каждом из конечного числа повторов игры. G: Одноходовая "дилемма заключенного"
Экономические интерпретации: • модели олигополии - Бертранa(Bertrand)и Курно( Сournot), • protection/ free trade, • уплата налогов(общественные блага), • соблюдение/нарушение квот в картеле, • реклама • environment/pollution. G(2): "Дилемма заключенного", повторяемая 2 раза.
Обратная индукция: выбор на первой фазе, в предположении, что в конечной, второй фазе избирается (defect,defect),т.е.выигрыш (1,1).Простоты ради полагаем здесь дисконт равным 1. В итоге: такое же равновесие в доминирующих стратегиях. Если равновесий по Нэшу несколько, ситуация несколько сложнее(см. Gibbons,с.84- 88). Если составная игра (astagegame) Gимеет единственное равновесие по Нэшу, то тогда, повторяя ее любое конечное число раз Т , т.е. рассматривая повторяемую игру G(T) , мы можем убедиться, что эта игра имеет лишь одно совершенное равновесие по Нэшу (SPNE), cовпадающее с равновесием по Нэшу в составной игреG. Для игр с конечным числом повторений Т усечение игры (subgame), начинающееся на ходе t +1, обозначают G(Т - t).Число таких усечений соответствует числу вариантов развития событий до моментаt . The Chainstore Paradox( Selten,1978) Рассмотрим игру, в которой 20 фирм стремятся последовательно войти на двадцать региональных рынков(по одной фирме на каждый рынок), монополизированных некоей сетью магазинов(incurbent). Поведение фирмы-монополиста, владеющей этой сетью магазинов, обозримо для фирм, стремящихся войти на рынки. Тем самым эта игра вполне соответствует описанию игр с конечным числом повторений, данному выше. Составная игра: 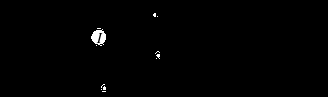 Казалось бы с тем, чтобы предотвратить попытки входа, фирме-монополисту следует создать себе репутацию, т.е. следует вести ожесточенную борьбу с фирмами , стремящимися войти на региональные рынки. Однако этот вывод не верен. Если новая фирма войдет на рынок, то укоренившейся фирма не будет ей препятствовать( и это известно фирме, стремящейся внедриться на рынок). Eсли на 19 рынках уже были предприняты попытки входа(нас в данном случае не интересует, как вела себя на них фирма, владеющая сетью магазинов ), то на двадцатом рынке следует выбрать стратегию Сollude. Далее методом обратной индукции мы приходим к равновесной по Нэшу паре стратегий "alwayscollude, alwaysenter". Эта пара не просто явялется NE , более того, она- SPNE. Другая равновесная по Нэшу пара стратегий "alwaysfight, neverenter" не является SPNE, т.к. это равновесие базируется на необоснованных угрозах укоренившейся фирмы. 2.3.2.ИГРЫ С БЕСКОНЕЧНЫМ ИЛИ НЕИЗВЕСТНЫМ ЧИСЛОМ ПОВТОРЕНИЙ( INFINITELYREPEATEDGAMES).СТРАТЕГИЯ КУРКА: РАВНОВЕСИЕ ПО НЭШУ И УСЛОВИЯ, СПОСОБСТВУЮЩИЕ УСТОЙЧИВОСТИ СОГЛАШЕНИЙ. СТРАТЕГИЯ "TIT-FOR-TAT". В играх с бесконечным(или неизвестным) числом повторений даже при существовании единственного равновесия по Нэшу итоговый выигрыш не может быть получен простым суммированием приведенных выигрышей. В такого рода играх возможно получение принципиально иного(чем в играх с известным конечным числом повторений) результата.Впереди всегда остается некая жизнь и, соответственно, - возможность воспользоваться выгодами кооперации.Именно кооперации, несмотря на то обстоятельство, что единственным равновесным по Нэшу исходом в stage game может быть(как в "дилемме заключенных") отказ от нее одновременно обоих игроков. Возможные равновесные(по Нэшу) стратегии игроков. 1. Стратегия предательства будет равновесной по Нэшу, ибо следование ей одним игроком предопределяет выбор подобной стратегии и другим игроком(он не сможет выиграть, отклоняясь от этой стратегии). Проблема состоит лишь в крайней невыгодности подобного равновесия для обеих сторон. 2. Стратегия наказания за предательство- "стратегия курка" или "стратегия предохранителя"(triggerstrategy) , иногда называемая также "мрачная стратегия(grimstrategy)":
Для того, чтобы доказать, что пара таких стратегий образуют равновесие по Нэшу, покажем, что коль скоро один игрок придерживается подобной стратегии, другому не остается ничего иного, как последовать его примеру. Нетрудно догадаться, что для этого необходимо наложить некоторые ограничения на размер дисконт - фактора Несложно определить критические значения параметров.Например, если в результате предательства игрок получил в некоторой игре | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
