Зертхан жумыстар Электр (1). 5 Зертханалы жмыстарды орындауа арналан дістемелік нсаулар 1 Зертханалы жмыс Электротехника
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
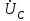 тоқ векторынан π/2 қалып қояды. тоқ векторынан π/2 қалып қояды.Векторлар суммасы теңдеуге сай болуы керек U=UR+UL+UC. ОАВ тікбұрышты үшбұрышынан Кирхгофтың екінші заңы бойынша тізбек теңдеуі (сур 6.1) келесідей болады: 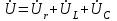 , (6.2) , (6.2)мұндағы 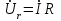 , , 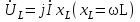 , , 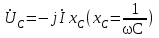 . .Ауыстырулардан кейін теңдеу (6.2) мына түрде болады: 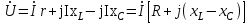 . .Осыдан 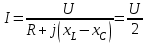 . (6.3) . (6.3)мұндағы 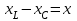 - тізбектің реактивті кедергісі, - тізбектің реактивті кедергісі,z – тізбектің жалпы кедергісі; 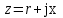 - тізбектің толық комплекстік кедергісінің алгебралық түрі; - тізбектің толық комплекстік кедергісінің алгебралық түрі;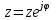 тізбектің толық комплекстік кедергісінің көрсеткіштік түрі, тізбектің толық комплекстік кедергісінің көрсеткіштік түрі, мұндағы 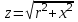 , ал , ал 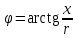 . .Реактивті кедергінің шамасына байланысты үш режим айырады: 1. Егер 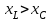 , онда , онда 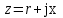 - тізбек активті-индуктивті. - тізбек активті-индуктивті.2. Егер 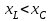 , онда , онда 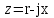 - тізбек активті-сыйымдылықты. - тізбек активті-сыйымдылықты. 3. Егер 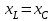 , онда , онда 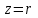 - тізбек активті. - тізбек активті. Кернеу резонансы Егер 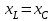 , онда тізбектегі тоқ , онда тізбектегі тоқ 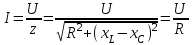 , яғни, тізбекте тек активті жүктеме R ғана бар сияқты тізбектің кедергісі өте төмен. Сонымен қатар индуктивтілік пен сыйымдылықтағы кернеулер , яғни, тізбекте тек активті жүктеме R ғана бар сияқты тізбектің кедергісі өте төмен. Сонымен қатар индуктивтілік пен сыйымдылықтағы кернеулер 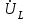 және және 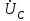 фаза бойынша π ығысқан (сур. 6.3). фаза бойынша π ығысқан (сур. 6.3).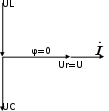 Сурет 6.3 Векторлық диаграмма Тізбекке салынған кернеу активті кедергідегі кернеуге тең және тоқ салынған кернеумен фаза бойынша сәйкес келеді. Сонымен қатар индуктивтілік пен сыйымдылықтағы кернеулер 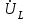 және және 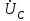 кіру кернеуінен кіру кернеуінен 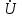 асады, сондықтан бұл құбылыс кернеу резонансы деп аталды. асады, сондықтан бұл құбылыс кернеу резонансы деп аталды.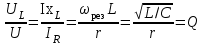 қатынасы контурдың төзімділігін білдіреді. Контурдың төзімділігі индуктивті элементтегі кернеудің екі полюсті схемаға кіру кернеуінен неше есе асатынын көрсетеді. Радиотехникада Q - 300 және одан да жоғары бола алады. Төзімділік неғұрлым жоғары болса, соғұрлым тоқ пен кернеу қисықтарының формасы тік болады. қатынасы контурдың төзімділігін білдіреді. Контурдың төзімділігі индуктивті элементтегі кернеудің екі полюсті схемаға кіру кернеуінен неше есе асатынын көрсетеді. Радиотехникада Q - 300 және одан да жоғары бола алады. Төзімділік неғұрлым жоғары болса, соғұрлым тоқ пен кернеу қисықтарының формасы тік болады.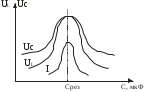 Сурет 6.4 Кернеу резонансының графигі 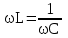 шартынан кернеу резонансына жиілік немесе индуктивтілік пен сыйымдылықты өзгерте отырып жетуге болатыны байқалады. Резонанс байқалатын бұрыштық жиілік резонансты бұрыштық жиілік деп аталады: шартынан кернеу резонансына жиілік немесе индуктивтілік пен сыйымдылықты өзгерте отырып жетуге болатыны байқалады. Резонанс байқалатын бұрыштық жиілік резонансты бұрыштық жиілік деп аталады: 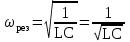 . Зертханада кернеу резонансына ω=const, L=const болғанда, С өзгерте отырып жетеді (сур. 6.4). EWB программасы кез-келген аталған параметрлерді өзгерткенде резонанс құбылысын байқауға мүмкіндік береді. . Зертханада кернеу резонансына ω=const, L=const болғанда, С өзгерте отырып жетеді (сур. 6.4). EWB программасы кез-келген аталған параметрлерді өзгерткенде резонанс құбылысын байқауға мүмкіндік береді.Кернеу резонансы кезінде келесі моменттерді атап өту керек: 1. Кернеу резонансы тек кіру кедергісі активті болған жағдайда байқалады, яғни: 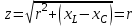 , , 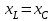 болғанда. Резонанс кезінде тоқ пен кіру кернеуі фаза бойынша дәл келеді. болғанда. Резонанс кезінде тоқ пен кіру кернеуі фаза бойынша дәл келеді.2. Резонанс L, C және ω тәуелді 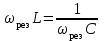 , немесе , немесе 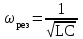 . .3. Кернеу мен кернеудің түсуі тең болады 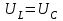 , ( , (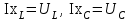 ). ). Жұмыстың мазмұны 1. Келесі параметрлерді өзгерте отырып, кернеу резонансына жету: а) кіру кернеуінің бұрыштық жиілігін; б) конденсатор сыйымдылығын; в) катушка индуктивтілігін. 2. Өзгертілген параметрлерден тоқ пен кернеудің резонанстық қисықтарының тәуелділігін көрсету. 3. Нәтижелер бойынша үш режим үшін векторлық диаграмма құру: а) резонансқа дейін; б) резонанс кезінде; в) резонанстан кейін. 4. Жасалған тәжірибе негізінде қорытынды жасау. Жұысты орындауға нұсқау 6.5 суретте көрсетілген R, L, C элементтерінің схемасын зерттеу үшін жинақтау. 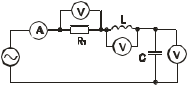 Сурет 6.5 Резистор, индуктивтілік катушка және конденсатор қосылысының схемасы Кернеу тұрақты күйінде қалады. Нәтижені 6.1, 6.2, 6.3 кестелеріне енгізеді. Кесте 6.1- Конденсатор сыйымдылығын өзгерткендегі өлшеу нәтижесі
Кесте 6.2- Кіру кернеуінің бұрыштық жиілігін өзгерткендегі өлшеу нәтижесі
Кесте 6.3- Катушка индуктивтілігін өзгерткендегі өлшеу нәтижесі
EWB программасындағы жұмыс барысы: Пиктограмма қатарынан керек элементтерді таңдап, номиналдарын қойып, бір-бірімен жалғаймыз (зерт.жұм. № 1, 2 қара). R, L, C элементтерін тізбектей жалғауды зерттейтін электр схемасының виртуальды моделі (сур. 6.6). 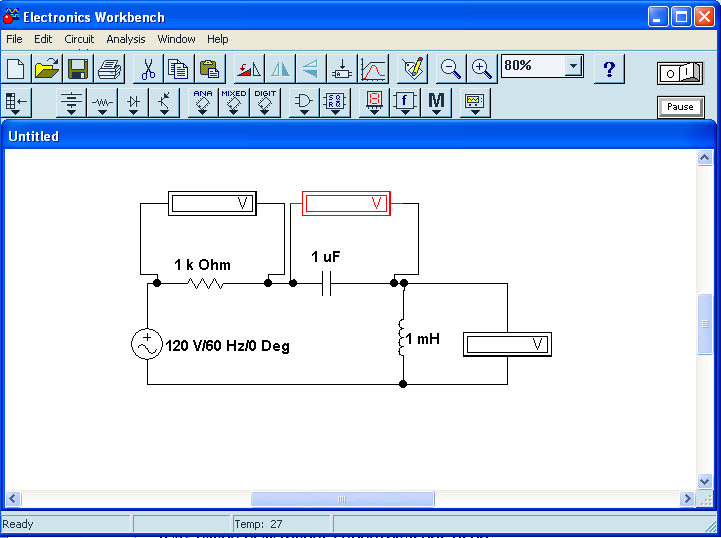 Сурет 6.6 R, L, C элементтерін тізбектей жалғауды зерттейтін электр схемасының виртуальды моделі Бақылау сұрақтары R, L, C-элементтері тізбектеп жалғанған тізбектің толық және толық кедергісінің комплексін қалай анықтауға болады. Олардың айырмашылығы қандай? Комплекстік сандарды қолданбай R, L, C элементтері тізбектеп жалғанған тізбекте тоқты қалай анықтауға болады? Бастапқы берілгендер ретінде не белгілі болу қажет? Қандай режимды резонансты деп атайды? Қандай шарттарда резонанс болады? R, L, C-элементтері тізбектей жалғанғанда резонансты режимды неге тоқ резонансы емес кернеу резонансы деп атайды? Резистор мен конденсатор тізбектей жалғанса резонанс режимы байқалады ма? Кернеу резонансына жеткенін құралдар арқылы қалай байқауға болады? Неліктен реалды индуктивті катушканың кернеуі конденсатор кернеуінен асады? Векторлық диаграммаларды қандай мақсатпен пайдаланады? Тізбектің қуат коэффициенті нені білдіреді? Ұсынылған әдебиеттер Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Москва, Гардарики, 2000. Сборник задач по ТОЭ Под. ред. Л. А. Бессонова. Москва Методические указания к выполнению лабораторных работ. Электрические цепи синусоидального тока. Жаутиков Б.А., Карманов С-К.Г., Айкеева А.А., КарГТУ 2003. СӨЖ үшін бақылау тапсырмалар Нақты зертханалық жұмыс бойынша негізгі түсініктер мен анықтамаларды оқу Кернеу резонансын зерттеу Тоқ резонансын зерттеу [3] сәйкес зертханалық жұмыс отчетын дайындау. Зертханалық жұмыс № 7 R, L, C элементтерін параллель қосу (2 сағат) Жұмыстың мақсаты: R, L, С элементтері параллель қосылған тізбекке талдау жасау, тоқ резонансын зерттеу, векторлық диаграмма құруды үйрену. Жалпы мәліметтер Үш жүктеме болсын (сур. 7.1). Бірінші жүктеме активті-индуктивті, екінші – активті-сыйымдылықты, үшінші – тек активті, яғни, 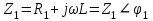 , , 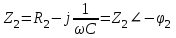 , , 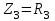 . .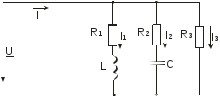 Сурет 7.1. Параллель қосылған жүктемелер Параллель қосылған жүктемелердің негізгі векторы болып кернеу векторы табылады, 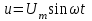 . .Кирхгофтың бірінші заңы бойынша лездік мәндер үшін: 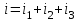 . Әсерлік мәндер үшін: . Әсерлік мәндер үшін: 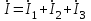 . .7.2 суретінде қарастырылатын тізбектің векторлық диаграммасы құрылған. Бірінші тармақ активті-индуктивті болғандықтан тоқ кернеуден артта қалады. Екінші тоқ кернеуді φ2 бұрышқа озады және үшінші тоқ кернеумен фаза бойынша дәл келеді. 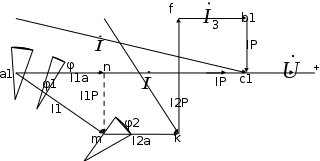 Сурет 7.2 Тізбектің векторлық диаграммасы Сондағы 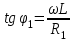 , , 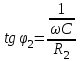 . .Кез-келген тармақтың тоғы, сонымен қатар жалпы тоқ активті және реактивті құраушыларға бөлінеді. 7.2 суретіндегі үшбұрыштар а1nm, mfk, а1в1с1- тоқ үшбұрыштары. Жалпы тоқ: 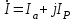 . (а) . (а)Теңдеуді құрайтын компоненттерді (а) жеке-жеке қарастырайық: 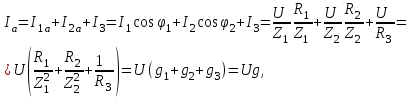 (б) (б)мұндағы g1, g2, g3, - тармақтардың активті өткізгіштері, g – тізбектің активті өткізгіші. 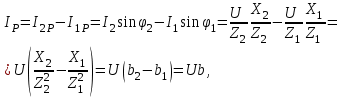 (в) (в)мұндағы b1, b2 и b – тармақтардың реактивті өткізгіштері, b – тізбектің реактивті өткізгіші. (б) және (в) теңдеулерін (а) теңдеуінде көрсетеміз: 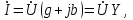 (7.1) (7.1)мұндағы Y – тізбектің толық өткізгіші. 7.3 суретінде 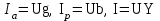 болғандықтан, өткізгіштер үшбұрышы келтірілген. болғандықтан, өткізгіштер үшбұрышы келтірілген.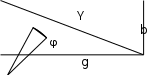 Сурет 7.3 Өткізгіштер үшбұрышы Тоқтар резонансы 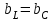 немесе немесе 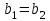 шарты орындалғанда (сур.7.4) тоқ резонансы болады шарты орындалғанда (сур.7.4) тоқ резонансы болады |

 рез
рез