Атаки на эллиптические кривые
 Скачать 191.67 Kb.
|
Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 426389
При анализе полученных данных из таблиц 4.1 – 4.10 можно заметить, что при выборе поля большого размера время, затраченное на атаку путем полного перебора, увеличивается. То есть криптостойкость алгоритмов растет с увеличением поля. Если была выбрана кривая над бинарным конечным полем как в таблице 4.7, 4.8, то можно заметить, что время кодирования и декодирования уменьшается, по сравнению с эллиптическими кривыми над полем простого числа. При этом были выбраны поля равные по длине. Так же можно заметить, что при выборе бинарного конечного поля криптостойкость алгоритма не сильно уменьшилась. Из этого можно сделать вывод, что при выборе поля одинаковой длинны, алгоритм, который использует бинарное конечное поле будет выполняться чуть быстрее. Выигрыш в скорости получается из-за того, что вычисления на компьютере происходят быстрее если числа, над которыми происходят операции могут быть представлены в виде степени двойки. Проанализировав графики 4.1, 4.2, 4.3, 4.4 можно заметить, что время, затраченное на вычисление открытого ключа, возрастает при выборе большего поля в обоих алгоритмах шифрования.
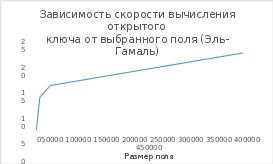    Секунды Секунды Рис. 4.1 Зависимость скорости вычисления открытого ключа от выбранного поля (Эль-Гамаль)
 Рис. 4.2 Зависимость скорости вычисления открытого ключа от выбранного поля (Диффи-Хеллман)
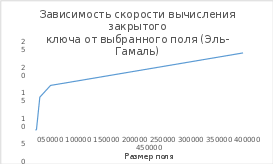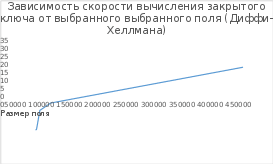  Секунды Секунды Рис. 4.3 Зависимость скорости вычисления закрытого ключа от выбранного поля (Диффи-Хеллман)
 Рис. 4.4 Зависимость скорости вычисления закрытого ключа от выбранного поля (Диффи-Хеллман) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
