ЖБК 200 вопросов и ответов. Бетон, арматура и железобетон

• Название: Бетон, арматура и железобетон
• Анкор: ЖБК 200 вопросов и ответов.doc
• Дата: 07.02.2017
• Размер: 11.86 Mb.
• Имя файла: ЖБК 200 вопросов и ответов.doc
• Тип: Документы; #2374
• страница: 11 из 53

47. ЧТО ТАКОЕ КОЭФФИЦИЕНТ ТОЧНОСТИ НАТЯЖЕНИЯ?

В производстве любых изделий могут быть неточности, которые заранее учитывают и допускают в ограниченных размерах. Одной из них при изготовлении преднапряженных изделий является погрешность в натяжении арматуры, что вызывает увеличение или уменьшение величины предварительного напряжения _sp по сравнению с расчетной – это учитывается умножением_sp на коэффициент точности натяжения _sp. Если неблагоприятное влияние на работу конструкции оказывает пониженное значение _sp (например, на образование трещин в зоне, растянутой при эксплуатации), то _sp < 1; если повышенное (например, на прочность в стадии обжатия), то_sp > 1. При подсчете потерь напряжений, ширины раскрытия трещин и прогибов допускается принимать _sp = 1. Значения _sp приведены в Нормах проектирования.

Не следует путать _sp с допустимым отклонением p. Если p используют при назначении проектной величины предварительного напряжения, то _sp – при расчете непосредственно самих сечений.

48. ПОЧЕМУ ПОЛОЖЕНИЕ СИЛЫ ОБЖАТИЯ Р НЕ ВСЕГДА СОВПАДАЕТ С  ЦЕНТРОМ ТЯЖЕСТИ НАПРЯГАЕМОЙ АРМАТУРЫ?

Усадка и ползучесть бетона вызывают не только потери напряжений в напрягаемой арматуре, но и сжимающие напряжения в ненапрягаемой арматуре _s и _s(рис. 22). В результате, после вторых потерь сила обжатия Р из усилия натяжения арматуры превращается в равнодействующую всех внутренних сил в сечении: Р = _spA_sp _sA_s _sA_s, а ее эксцентриситет относительно центра тяжести (ц.т.) сечения равен

е_ор= (_spA_spy_sp_sA_sy_s+ _sA_sy_s) /P, т.е. не совпадает с y_sp. Напряжения _s и _sв ненапрягаемой арматуре определяют по тем же формулам Норм, что и потери напряжений ₈ и ₉ в напрягаемой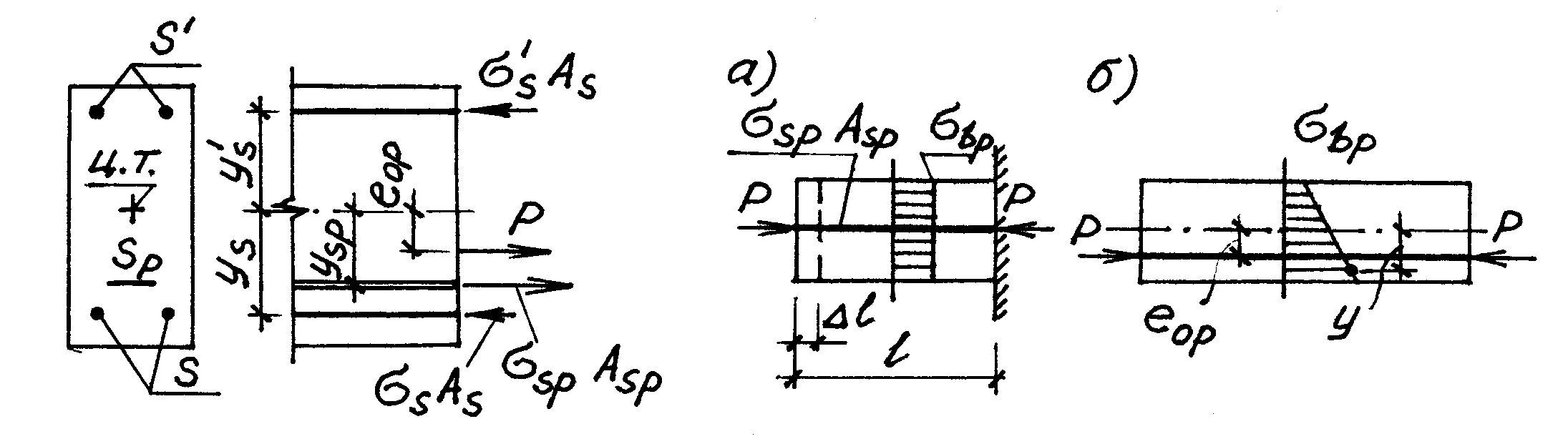

Рис.22

Рис.23

49. ЧТО ТАКОЕ ПРИВЕДЕННЫЕ СЕЧЕНИЯ?

Бетон и арматура, хотя и работают совместно, но имеют разные модули упругости: при одинаковых деформациях в них возникают разные напряжения. Чтобы подсчитать их, сечения приводят к одному материалу (обычно к бетону) через коэффициент приведения  = Е_s / E_b, где Е_s и Е_b – модули упругости арматуры и бетона (начальный). Такие сечения называют приведенными. Поясним примером.

Требуется определить напряжения в бетоне преднапряженного элемента, обжатого осевой силой Р = _spA_sp, где А_sp – площадь сечения напрягаемой арматуры. После обжатия элемент упруго укорачивается на величину l, или _b = l/ l (рис. 23,а), причем вместе с бетоном укорачивается и напрягаемая арматура: _sp = _b. Усилие в ней падает на величину Р = _spA_sp = _spE_sA_sp.

Поскольку _sp = _b, а Е_s = Е_b, то _sp= _spE_s = _bE_b = (_bp/E_b)E_b= =_bp, где _bp – установившееся напряжение в бетоне. Условие равновесия: Р – Р = N_bp, или Р = N_bp + P, где N_bp=_bpA_b  усилие, воспринимаемое бетоном, А_b – площадь бетонного сечения, Р = _spA_sp =_bpA_sp. Отсюда Р = _bpА_b +_bpA_sp = _bpA_red, где А_red =А_b + A_sp  площадь приведенного сечения. Тогда _bp = P/A_red.

Следовательно, чтобы вычислить напряжения в бетоне при обжатии, вовсе не обязательно учитывать упругое укорочение арматуры и падение в ней усилия Р  достаточно первоначальное значение Р поделить на площадь приведенного сечения.

В более сложных случаях одной площади недостаточно. Например, чтобы вычислить _bp в любой точке приведенного сечения при внецентренном обжатии (рис. 23,б) требуется знать статический момент S_red (для нахождения центра тяжести приведенного сечения) и момент инерции J_red. Тогда _bp = Р/A_red  Pe_opy/J_red, где y – расстояние от центра тяжести до интересующей точки.