математические методы в психологии. мат.методы в психологии Ушакова А.И.. Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы

• Название: Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы
• Анкор: математические методы в психологии
• Дата: 27.05.2022
• Размер: 414.5 Kb.
• Имя файла: мат.методы в психологии Ушакова А.И..doc
• Тип: Вопросы к экзамену; #553323
• страница: 5 из 6

Дж. Гласc и Дж. Стэнли приводят сводную таблицу для демонстрации возможных сочетаний типов шкал для измеряемых переменных, между которыми подсчитывается коэффициент корреляции.

Выбор меры связи определяется двумя моментами:

1) обоснованием типа шкал для каждой из переменных;

2) обоснованием соответствия способа определения коэффициента тем или иным допущениям теоретического плана.

Подсчет коэффициентов корреляции при обработке данных в экспериментальных, квазиэкспериментальных и собственно корреляционных исследованиях включен в разные планы обработки данных.

В зависимости от конкретизации способов обработки данных количественная оценка взаимосвязи может характеризовать полученные эффекты как достаточно четко установленные или, напротив, недостаточно явные, не удовлетворяющие по величине той их роли, которая предполагалась в гипотезе исследования.

27.Корреляционный анализ: сущность корреляционного анализа, задачи решаемые в психологии методами корреляционного анализа, диаграмма рассеивания.

Корреляционный анализ – это проверка гипотез о связях между переменными с использованием коэффициентов корреляции, двумерной описательной статистики, количественной меры взаимосвязи (совместной изменчивости) двух переменных. Таким образом, это совокупность методов обнаружения корреляционной зависимости между случайными величинами или признаками.

Корреляционный анализ для двух случайных величин заключает в себе:

• 
  построение корреляционного поля и составление корреляционной таблицы;
  
• 
  вычисление выборочных коэффициентов корреляции и корреляционных отношений;
  
• 
  проверку статистической гипотезы значимости связи.
  

Основное назначение корреляционного анализа – выявление связи между двумя или более изучаемыми переменными, которая рассматривается как совместное согласованное изменение двух исследуемых характеристик. Данная изменчивость обладает тремя основными характериcтиками: формой, направлением и силой.
Целью корреляционного анализа является выявление оценки силы связи между случайными величинами (признаками), которые характеризует некоторый реальный процесс.
Задачи корреляционного анализа:

а) Измерение степени связности (тесноты, силы, строгости, интенсивности) двух и более явлений.
б) Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями. Существенные в данном аспекте факторы используют далее в регрессионном анализе.
в) Обнаружение неизвестных причинных связей.

Формы проявления взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи.
Корреляционная связь проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятностных значений независимой переменной. Связь называется корреляционной, если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака.
28.Корреляционный анализ, построение корреляционных графов и плеяд.

Корреляционный анализ – это проверка гипотез о связях между переменными с использованием коэффициентов корреляции.

Коэффициент корреляции – это мера прямой или обратной пропорциональности между двумя переменными. Он чувствителен к связи только в том случае, если эта связь является монотонной – не меняет направления по мере увеличения значений одной из переменных.

Основные показатели:

а) сила – определяется по абсолютной величине корреляции (меняется от -1 до 1);

б) направление связи – определяется по знаку корреляции: положительный – связь прямая, тогда как отрицательный – связь обратная;

в) надежность (достоверность) связи – определяется р-уровнем статистической значимости (чем меньше р-уровень, тем выше статистическая значимость, достоверность связи).

В качестве условий применения коэффициента корреляции выделяют:

● переменные измерены в количественной (ранговой, метрической) шкале на одной и той же выборке объектов;

● связь между переменными является монотонной.

После того как были выявлены статистически значимые корреляционные связи, их можно представить графически в виде корреляционной плеяды или плеяд.

Корреляционная плеяда – это фигура, состоящая из вершин и соединяющих их линий. Вершины обычно соответствуют признакам и обозначаются цифрами – номерами переменных. Линии соответствуют статистически достоверным связям и графически выражают знак, а иногда и р - уровень значимости связи (10).

Пример:Построение корреляционной плеяды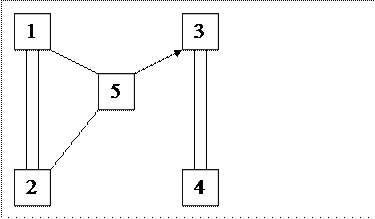



Примечание: 1 - напряженность в отношениях, 2 – отчужденность в отношениях, 3 – агрессия в отношениях, 4 – конфликтность в отношениях, 5 – степень дисгармоничности отношений

 р≤0,001; р≤0,01; р≤0,05

Посторенние плеяды начинают с переменной, имеющей наибольшее число значимых связей, постепенно добавляя в рисунок другие переменные – по мере убывания числа связей, связывая их линиями, соответствующими связям между ними.

 Корреляционные плеяды используются как наглядный способ представления результатов корреляционного анализа. Это не отдельный статистический метод, а лишь способ графически представить корреляционные взаимосвязи.

Существует два основных способа построения корреляционных плеяд:

1. 
   Рисование с помощью инструментов Word.
   
2. 
   Построение при помощи специальных программ.
   

Существует несколько программ для построения корреляционных плеяд. При этом в строго научной терминологии корреляционные плеяды называются графами.

Графы – это совокупность некоторых объектов, соединенных связями. Применительно к психологии корреляционные связи между психологическими показателями – это и есть графы.

Суть программ построения граф сводится к тому, что в некотором редакторе в определенном формате нужно задать психологические показатели, связи между ними и программа сама нарисует корреляционную плеяду наиболее оптимально расположив объекты.


29.Регрессионный анализ. Сущность регрессионного анализа. Примеры применения регрессионного анализа в психологических исследованиях.

Регрессионный анализ (РА) представляет собой совокупность статистических методов обработки результатов испытаний, позволяющих в условиях стохастической зависимости выходной (изучаемой) переменной от входных (объясняющих) факторов, определять данную зависимость.

Рассматривают две модели регрессионного анализа [2, 3, 54]. В первой модели зависимая переменная Y — случайная переменная, а независимые переменные xv х2,..., хк — не случайные переменные. Модель регрессионного анализа имеет вид



Во второй модели как зависимая переменная Y, так и независимые переменные Xv Х2, ..., Xfc являются случайными величинами, а функция отклика имеет вид



Исследования в рамках второй регрессионной модели проводят, как правило, с привлечением методов корреляционного анализа.

Сущность регрессионного анализа состоит в замене стохастической зависимости между переменными Y и xv х2, ..., хк некоторой детерминированной зависимостью, которая достаточно хорошо аппроксимирует основные свойства исходной стохастической зависимости. В регрессионном анализе используется детерминированная форма причинно-следственной зависимости; форма, при которой устанавливается аналитическая зависимость между некоторой характеристикой случайной величины Y и независимыми переменными , х2,..., хк. В качестве такой характеристики в регрессионном анализе используется условное математическое ожидание выходной переменной Y при условии, что входные переменные xv х2, ..., хк приняли определенные значения. Таким образом, сущность регрессионного анализа состоит в замене зависимостей вида (9.1) или (9.2) зависимостью вида

30.Анализ данных на компьютере. Виды статистических пакетов. Характеристика пакета SPSS, общий обзор пакета. Создание файла данных.

Рассмотрим и средства статистического анализа, позволяющие построить формальные математические модели процессов (обычно без анализа механизмов функционирования систем) и, при необходимости, осуществить прогноз их поведения при различных сочетаниях влияющих параметров. Это касается также прогнозов на основании временных рядов.

Все программы статистической обработки данных можно разделить на профессиональные, полупрофессиональные (популярные) и специализированные. Статистические программы относятся к наукоемкому программному обеспечению, цена их часто недоступна индивидуальному пользователю. Профессиональные пакеты имеют большое количество методов анализа, популярные пакеты - количество функций, достаточное для универсального применения. Специализированные же пакеты ориентированы на какую-либо узкую область анализа данных.

MS Excel является самым часто упоминаемым и используемым приложением из пакета офисных программ компании Microsoft MS Office. MS Excel широко распространен, имеет русскоязычную версию, тесно интегрирован с MS Word и PowerPoint. При этом, MS Excel - это электронная таблица с достаточно мощными математическими возможностями, где некоторые статистические функции являются просто дополнительными встроенными формулами. Расчеты сделанные при ее помощи не признаются авторитетными, и невозможно построить качественные научные графики. Безусловно, MS Excel хорошо подходит для накопления данных, промежуточного преобразования, предварительных статистических прикидок, для построения некоторых видов диаграмм. Однако окончательный статистический анализ необходимо делать в программах, которые специально созданы для этих целей. Существует макрос-дополнение XLSTAT-Pro http://www.xlstat.com для MS Excel который, включает в себя более 50 статистических функций, включая анализ выживаемости, которых в основных случаях достаточно для обычного применения.

Ранее одним из наиболее популярных пакетов был Statgraphics. В нем удобно сочетаются достаточно мощные средства статистического анализа и визуализации результатов. Собственно этот пакет и сейчас широко используется, причем не только в учебном процессе, но и в научных исследованиях.

В настоящее время из статистических пакетов в России вероятно шире всего используются STATISTICA, STADIA и SPSS. Их популярности способствуют: большое количество реализованных методов; хорошая русификация; наличие учебной и справочной литературы по работе с ними.

Такие пакеты являются универсальными и предназначены для решения широкого круга задач. Универсальные пакеты содержат такие разделы математической статистики, как описательная статистика, парные критерии, анализ факторных эффектов, корреляционный анализ, регрессионный анализ, анализ времен рядов, многомерные методы, методы контроля качества и др.

Парные критерии оценивают различия между двумя совокупностями данных. Типичная задача в этом разделе — определение влияния нововведения, сделанного на предприятии, на результаты работы.
Еще одна важная задача, которую позволяют решать универсальные пакеты, — это прогнозирование, например, курса валют. Все пакеты содержат развитые средства регрессионного анализа.
Многомерные методы — дискриминантный, кластерный, факторный анализы и шкалирование — помогают понять, нет ли какой-либо закономерности или группировки в и множестве объектов. Многомерные методы позволяют по экономическим показателям образовать группы сходных предприятий.

SPSS (Statistical Package for Social Science). Самый часто используемый пакет статистической обработки данных с более чем 30-и летней историей http://www.spss.com Отличается гибкостью, мощностью применим для всех видов статистических расчетов применяемых в биомедицине. Недавно вышла 13-я англоязычная версия. Существует русскоязычное представительство компании http://www.spss.ru которое предлагает полностью русифицированную версию SPSS 12.0.2 для Windows. Появился учебник на русском языке, позволяющий шаг за шагом освоить возможности SPSS, репетитор по статистике на русском языке, помогающий в выборе нужной статистической или графической процедуры для конкретных данных и задач, а также справка по SPSS Base и SPSS Tables.
31.Назначение дисперсионного анализа. Примеры применения дисперсионного анализа в психологических исследованиях. Сущность дисперсионного анализа и основные этапы его проведения.
Дисперсионный анализ – метод статистического исследования, с помощью которого изучается влияние отдельных факторов на результативный показатель. Он позволяет среди множества факторов выделить один и оценить его влияние на вариацию результативного признака и влияние всех других факторов в совокупности на вариацию результативного признака.

Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.

Этапы проведения дисперсионного анализа:

1. Определяется множество факторов, потенциально влияющих на Y.

2. Из всех факторов выделяется один основной.

3. Проводится группировка всей совокупности данных по выбранному признаку (число, интервал).

4. Рассчитывается общая дисперсия Y(по всей совокупности):  .

5. Рассчитывается межгрупповая дисперсия – характеризует вариацию Yпод влиянием фактора, положенного в основу группировки:  ,

где: nj – объем группы;   – среднее значение признака внутри группы.

6. Вариация Yпод влиянием прочих факторов оценивается с помощью средней из внутригрупповых дисперсий:  .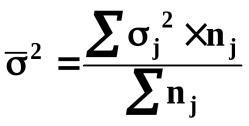

7. Проверка: сумма межгрупповой дисперсии и средней из внутригрупповых дисперсий должна равняться общей дисперсии (теорема сложения дисперсии):  .

8. Правильность выбора фактора оценивается с помощью относительных показателей вариации:

– коэффициент детерминации:  – характеризует долю вариацииY, обусловленную влиянием фактора (например, 70% – т.е. 70% вариации Y объясняется влиянием фактора);

– эмпирическое корреляционное отношение:  – характеризует тесноту связи (по шкале Чеддока).

Как правило, дисперсионный анализ проводится итеративным способом, когда происходит последовательный анализ влияния факторов на Yдо тех пор, пока не будут определены наиболее важные факторы.

32.Назначение факторного анализа. Задачи, решаемые методами факторного анализа в психологии. Сущность факторного анализа. Основные понятия факторного анализа: факторные нагрузки, общности, специфичности.
Под факторным анализом (диагностикой) понимается методика и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа:

• детерминированный (функциональный) и стохастический (корреляционный);

• прямой (дедуктивный) и обратный (индуктивный);

• одноступенчатый и многоступенчатый;

• статический и динамический;

• ретроспективный и перспективный (прогнозный).

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с резуль­тативным показателем носит функциональный характер, т.е. ре­зультативный показатель может быть представлен в виде произ­ведения, частного или алгебраической суммы факторов.

Стохастический факторный анализ представляет собой методику иссле­дования влияния факторов, связь которых с результативным показателем в отличие от функциональной является неполной, ве­роятностной (корреляционной).

При прямом факторном анализе исследование ведется дедук­тивным способом - от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных свя­зей способом логичной индукции - от частных, отдельных факто­ров к обобщающим.

Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детали­зации на составные части. Например, у = а - b. При многоступен­чатом факторном анализе проводится детализация факторов а и b на составные элементы с целью изучения их поведения. Дета­лизация факторов может быть продолжена дальше. В данном случае изучается влияние факторов различных уровней соподчиненности.

Статический анализ применяется при изучении влияния фак­торов на результативные показатели на соответствующую дату. Динамический анализ представляет собой методику исследования причинно-следственных связей в динамике.

Ретроспективный факторный анализ изучает причины изме­нения результативных показателей за прошлые периоды, а перс­пективный - исследует поведение факторов и результативных по­казателей в перспективе.