Основные Тесты с ответами. I. Теоретические вопросы Агрегированные величины представляют собой

• Название: I. Теоретические вопросы Агрегированные величины представляют собой
• Дата: 26.08.2022
• Размер: 1.08 Mb.
• Имя файла: Основные Тесты с ответами.doc
• Тип: Документы; #654112
• страница: 5 из 7

Если реальный ВНД = 270 млн. руб. ,уровень циклической безработицы = 5 % , коэффициент чувствительности ВНД к циклической безработице = 2 , то по закону Оукена потенциальный ВНД равен 300 млн.руб.

Решение:

1. 
   Отставание реального ВНД (Y) от потенциального (Yf) = 5 % х 2 (коэффиц. чувствительности)= 10 %
   
2. 
   Определяем Yf =[Y :(100 % – Отставание Y от Yf)] х 100 % = [270 :(100 % – 10 %)] х 100 % = 300
   

Если реальный ВНД = 340 млн. руб., уровень циклической безработицы = 5 % , коэффициент чувствительности ВНД к циклической безработице = 3 , то по закону Оукена потенциальный ВНД равен 400 млн.руб.

Решение:

1. 
   Отставание реального ВНД (Y) от потенциального (Yf) = 5 % х 3 (коэффиц. чувствительности)= 15 %
   
2. 
   Определяем Yf =[Y :(100 % – Отставание Y от Yf)] х 100 % = [340 :(100 % – 15 %)] х 100 % = 400
   

Если реальный ВНД=340 млн. руб., уровень фактической беработицы=7%, естественный уровень безработицы=2%, коэффициент чувствительности ВНД к циклической безработице =3, то экономические потери от безработицы, согласно закону Оукена равны 60 млн. руб.

Решение:

1. 
   Циклическая безработица = 7 % - 2 % = 5 %
   
2. 
   Экономические потери от безработицы, т.е. отставание реального ВНД (Y) от потенциального (Yf) = 5 % х 3 (коэффиц. чувствительности)= 15 % (или 0,15, если не в %)
   
3. 
   Определяем Yf =[Y : (100 % – Отставание Y от Yf)] х 100 % = [340 :(100 % – 15 %)] х 100 % = 400
   
4. 
   Определяем Экономические потери от безработицыY=15 % Yf = 400 х 0,15 = 60
   

Если рента с земельного участка в 10га составила за год 150 тыс. руб., а ставка банковского процента равна 8%, то цена этого земельного участка будет _____ тыс. руб.

1. 
   1725
   
2. 
   1500
   
3. 
   1875
   
4. 
   1250
   

Решение:

Цена земли (ЦЗ) = (Рента (R) : %) х 100 % ;  ЦЗ = (150 тыс. : 8%) х 100 %= 1875 тыс.
Если спрос на продукцию фирмы- монополиста имеет вид Qd=40-P (Qd-величина спроса, шт.P-цена .руб. за шт.), а функция средних издержек AC(Q)=2Q+10(в руб. ) , то цена, при которой монополист максимизирует валовой доход, равна 35руб.

Решение:

1. Доход монополиста максимизируется при P=MR=MC

2. MC= ТС_(Q)΄; TC= AC x Q = (2Q+10) x Q = 2Q²+10Q

3. Т.к. TC= 2Q²+10Q  MC= 4Q + 10

4. Qd= 40 – P  P = 40 – Q  MR= 40 – 2Q

5. Максимизация вал. Дохода при MR= MC  40 – 2Q=4Q + 10; Q=5

6. Находим Pmax (cм.4)= 40 – Q= 40-5=35
Если спрос на продукцию фирмы-монополиста имеет вид Qd=106-P(Qd-величина спроса ,шт., P- цена , руб. за шт.), а функция средних издержек AC(Q)= 5Q+10 ( в руб.), то максимальная цена , при которой монополист не несет убытков, равна 94 руб.

Решение:

1. Монополист не несет убытков при P=MR=MC

2. MC= ТС_(Q)΄; TC= AC x Q = (5Q+10) x Q = 5Q²+10Q

3. Т.к. TC= 5Q²+10Q  MC= 10Q + 10

4. Qd= 106 – P  P = 106 – Q  MR= 106 – 2Q

5. Убытков нет при MR= MC  106 – 2Q=10Q + 10; Q=12

6. Находим Pmax (cм.4)= 106 – Q= 106 - 12=94
Если спрос на продукцию фирмы- монополиста имеет вид Qd=40-P (Qd-величина спроса, шт.P-цена .руб. за шт.), а функция средних издержек AC(Q)=2Q+10(в руб. ) , то оптимальный объем производства монополиста, максимизирующего прибыль, равен 5 шт.

Решение:

1. Объем производства монополиста оптимизируется при P=MR=MC

2. MC= ТС_(Q)΄; TC= AC x Q = (2Q+10) x Q = 2Q²+10Q

3. Т.к. TC= 2Q²+10Q  MC= 4Q + 10

4. Qd= 40 – P  P = 40 – Q  MR= 40 – 2Q

5. Максимизация прибыли при MR= MC  40 – 2Q=4Q + 10; Q=5
Если ставка ссудного процента составляет 5%, а рента равняется 400 тыс.руб., то цена земли составит 8000 тыс. руб.

Решение:

1. 
   Цена земли (ЦЗ) = (Рента (R) : %) х 100 % ;
   
2. 
   Определяем ЦЗ = (400 тыс. рубл. : 5 %) х 100 % = 8 000 тыс. рубл.
   

Если совокупный доход фирмы, производящей радиоприёмники, составляет 1000 ед. в месяц при объеме выпуска 500 штук, её постоянные издержки составляют 800 ден. единиц в месяц, а переменные – 100 ден. единиц в месяц, то её средняя прибыль равна …

1. 
   0,2 ден. единицы
   
2. 
   2 ден. единицы
   
3. 
   5 ден. единиц
   
4. 
   100 ден. единиц
   

Решение: ТR - общая выручка (совокупный доход); Pr – прибыль; Prср – средняя прибыль; FC – постоянные издержки; VC – переменные издержки.

1. Prср = Pr :Q; Pr = ТR – ТС = TR – FC - VC

2. Pr = 1000 – 800 – 100 = 100

3. Prср = 100 : 500 = 0,2
Если уравнение потребления имеет вид C=200+0,8Y (Y - совокупный объем производства и доходов), то при Y = 2000 млн. руб. средняя склонность к потреблению (АРС) равна 90 процентов.

Решение:

APC = C : Y = (200+0,8 х 2000) : 2000 = 0,9; в процентах: 0,9 х 100 % = 90 %
Если уравнение сбережений имеет вид S=(-20)+0,25 У (У - совокупный объем производства и доходов), то при У=100 млн.руб. средняя склонность к сбережению (APS) равна 5 процентов

Решение:

APS = S : Y  APS = (- 20+ 0,25 х 100): 100=0,05;  в процентах 0,05 х 100 %= 5 %
Если уравнение сбережений имеет вид S=(-40)+0,5 У (У - совокупный объем производства и доходов), то при У=200 млрд.руб. средняя склонность к потреблению (APC) равна 70 процентов

Решение:

1. APS + APC = 100 %;  APC = 100 % - APS;

Хэюъ.джд 2. APS = S : Y = [(-40) + 0,5 х 200] : 200 = 0,3;  в процентах 0,3 х 100 %= 30 %

3. APC = 100 % - 30 % = 70 %;
Если уравнение сбережений имеет вид S = (-50)+0,5Y, (Y – совокупный объем производства и доходов), то при Y=100 средняя склонность к потреблению (APC), равна 100 процентов

Решение:

1. APS + APC = 100 %;  APC = 100 % - APS;

2. APS = S : Y = [(-50) + 0,5 х 100] : 100 = 0 : 100 = 0. Т.е. сбережения вообще отсутствуют!

3. APC = 100 % - 0 % = 100 %;
Если участок земли площадью 12 га продается по цене 59 тыс. рублей за 1 га , а годовая процентная ставка составляет 6% , то участок приносит в течение года ренту, равную 42,48тыс. ден. ед.

Решение:

3. 
   Цена земли (ЦЗ) = (Рента (R) : %) х 100 % ; R =(ЦЗ х %) : 100 %
   
4. 
   Определяем ЦЗ = 59 тыс. рубл. х 12 = 708 тыс. рубл.
   
5. 
   R = (708 х 6%) : 100 % = 42,48 тыс.
   

Если участок земли площадью 12 га продается по цене 50 тыс. рублей за один гектар, а годовая процентная ставка составляет 6% , то участок приносит в течение года ренту , равную 36 тыс. ден. ед.

Решение:

1. 
   Цена земли (ЦЗ) = (Рента (R) : %) х 100 % ; R =(ЦЗ х %) : 100 %
   
2. 
   Определяем ЦЗ = 50 тыс. рубл. х 12 = 600 тыс. рубл.
   
3. 
   R = (600 х 6%) : 100 % = 36 тыс.
   

Если участок земли площадью 10 га продается по цене 8 тыс. рублей за один гектар, а годовая процентная ставка составляет 5% , то участок приносит в течение года ренту, равную 4тыс. ден. ед.

Решение: см. выше
Если функции спроса и предложения имеют вид: Qd=11-P, Qs=-4+2P(Qd-величина спроса, Qs-величина предложения,P-цена ,руб. за шт.), то после введения правительством налога с покупателей в размере 6 руб. за шт. равновесный объем продаж уменьшиться на 6 шт.

Решение: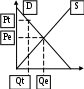

1. 
   Введение налога увеличивает для потребителей цену до Pt. Новый объем продаж будет определяться спросом потребителей, т.е функцией спроса (Qd=11-P).
   
2. 
   Находим равновесную цену (Pе). Qd=Qs, т.е. 11-P =-4+2P  3Р=15; Р(т.е. Ре)= 5
   
3. 
   Находим новую цену (Pt)= Ре + 6 = 11.
   
4. 
   Находим Qе (из формулы Qd) =11-Pе=11 – 5=6.
   
5. 
   Находим Qt (из формулы Qd) =11-P= 0.
   
6. 
   Находим разницу между Qt и Qе: Qgt – Qе=0-6= - 6.
   

Если функции спроса и предложения имеют вид: Qd=11-P, Qs= - 4+2P(Qd-величина спроса, Qs-величина предложения,P-цена ,руб. за шт.), то при установлении правительством фиксированной цены, равной 3 руб. за шт. объем продаж составит 2 шт.

Решение: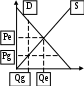

1. 
   Установление государством фиксированной цены ниже равновесной (до Pg) не позволяет производителям продать более Qg. Новый объем продаж будет определяться предложением производителей, т.е. функцией предложения (- 4+2P).
   
2. 
   Находим Qg (из формулы Qs) =- 4+2P = - 4+2 х 3= - 4 + 6=2
   

Если функции спроса и предложения имеют вид: Qd=11-P, Qs= - 4+2P(Qd-величина спроса, Qs-величина предложения,P-цена ,руб. за шт.), то после введения правительством субсидий для покупателей в размере 6 руб. за шт., равновесный объем продаж составит 18 шт.

Решение: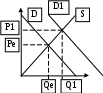

1. 
   Субсидии правительства увеличивают доход потребителей, что вызывает рост их спроса. Иными словами, формируется новая функция спроса, проявляющаяся в смещении D до D1. Очевидно, что новый объем продаж будет определяться либо функцией предложения (Qs= - 4+2P), либо новой функцией спроса.
   
2. 
   Определим первоначальную равновесную цену (Pе). Qd=Qs, т.е. 11-P =-4+2P  3Р=15; Р(т.е. Ре)= 5
   
3. 
   Находим цену Р1 = Ре + 6= 5 + 6= 11.
   
4. 
   Находим Q1 (из формулы Qs) =- 4+2P = - 4+2 х 11= - 4 + 22=18
   

Если функции спроса и предложения имеют вид: Qd=11-P, Qs= - 4+2P(Qd-величина спроса, Qs-величина предложения,P-цена ,руб. за шт.), то при установлении правительством фиксированной цены, равной 10 руб. , совокупный доход продавцов составит 10 руб.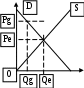

1. 
   Совокупный доход продавцов определяется количеством проданной продукции х на ее цену.
   
2. 
   Определим, превышает или ниже равновесной цена Pg= 10, установленная правительством. Ре = : Qd=Qs, т.е. 11-P =-4+2P  3Р=15; Р(т.е. Ре)= 5. Pg> Ре Q_g определяется функцией спроса Qd=11-P
   
3. 
   Определим Q_g =11 -P = 11 – 10=1
   
4. 
   Определим совокупный доход продавцов: Pg х Q_g = 10 х 1 = 10
   

Если функции спроса и предложения имеют вид: Qd=11-P, Qs= - 4+2P(Qd-величина спроса, Qs-величина предложения,P-цена ,руб. за шт.), то совокупные расходы покупателей на приобретение товара в условиях равновесия равны 30 руб.

1. 
   Совокупные расходы покупателей определяются количеством проданной продукции х на ее цену.
   
2. 
   Определим равновесную цену Ре = : Qd=Qs, т.е. 11-P =-4+2P  3Р=15; Р(т.е. Ре)= 5.
   
3. 
   Равновесный объем продаж определяется любой функцией, к примеру функцией спроса Qd=11-P
   
4. 
   Определим Q_е =11 -P = 11 – 5=6
   
5. 
   Определим совокупные расходы потребителей: Pе х Q_е = 5 х 6 = 30
   

Если функция спроса на продукцию монополиста P=20-Q, а функция общих затрат TC=2+4Q+Q², то цена , при которой монополист максимизирует прибыль, равна 16

Решение:

1. 
   Pmax при MR= MC
   
2. 
   P = 20 – Q  MR= 20 – 2Q; при этом Pmax определяется по формуле P = 20 – Q
   
3. 
   ТC(Q)=2 + 4Q+ Q²  MC=4 + 2 х Q
   
4. 
   MR= MC  20 – 2Q = 4 + 2Q  16 = 4 Q; Q=4
   
5. 
   Находим Pmax (cм.п.2)= 20 – Q= 20-4=16
   

Если функция спроса на продукцию монополиста P=16-Q, а функция общих затрат TC=2+4Q+Q², то цена , при которой монополист максимизирует прибыль, равна 13

Решение:

1. 
   Pmax при MR= MC
   
2. 
   P = 16 – Q  MR= 16 – 2Q; при этом Pmax определяется по формуле P = 16 – Q
   
3. 
   ТC(Q)=2 + 4Q+ Q²  MC=4 + 2 Q
   
4. 
   MR= MC  16 – 2Q = 4 + 2Q  12 = 4 Q; Q=3
   
5. 
   Находим Pmax (cм.п.2)= 16 – Q= 16 - 3=13
   

Если функция спроса Q_D=20-2P , то при цене товара, равной 3, излишек потребителя составит 49.

Решение:

1. 
   Излишек потребителя = площади треугольника РеЕD = 0,5 площади прямоугольника РеЕАD. Ре=3
   
2. 
   Определим 0D; Q_D=20-2P; Q_D = 0; 20-2P = 0; Р= 10 =0D
   
3. 
   Определим РеD; 0D – Ре= 10 – 3= 7
   
4. 
   Определим 0Qе из Q_D=20-2P при Р=3: 0Qе = 20 – 2 х 3 =14
   
5. 
   Площадь прямоугольника РеЕАD= 7 х 14=98.
   
6. 
   Площадь треугольника РеЕD = 0,5 х 98= 49
   

Если функция спроса Q_D=12-3P, то при цене товара, равной 2, излишек потребителя составит 6

Решение: см. выше.
Если функция спроса Q_D=16-4P, то при цене товара, равной 2 , излишек потребителя составит: 8

Решение: см. выше.
Если функция спроса задана уравнением QD=45-3Р, а функция предложения Qs= 2Р + 10, то излишек потребителя составит…

1. 
   110
   
2. 
   83
   
3. 
   96
   
4. 
   124
   

Решение:

1. Pe из 45-3Р = 2Р + 10; Pe = 7

2. Pо из 45-3Р следующим образом 0 = 45-3P; 45 = 3 P; P= 15 =Pо

3. Qe из 45-3Р равен 45 – 3 х 7 = 24

4. Площадь прямоугольника = 24 х (15 – 7) = 192

5. Площадь треугольника = 192 : 2 = 96
Если функция спроса на продукцию монополиста описывается уравнением P=60-Q, а функция общих издержек TC=10+Q², то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

1. 
   45 и 15
   
2. 
   43 и 17
   
3. 
   44 и 16
   
4. 
   46 и 14
   

Решение:

1. Pmax при MR= MC

2. P = 60 – Q;  MR= 60 – 2Q;

3. ТC(Q) = 10 + Q² ;  MC= 2 Q

4. Определяем объем продаж Q: MR= MC;  60 – 2Q = 2Q;  60 = 4 Q; Q=15

5. Находим P (cм.п.2)= 60 – Q = 60 - 15= 45
Если функция спроса на продукцию монополиста описывается уравнением P=80-5Q, а функция общих затрат TC=50+20Q, то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

1. 
   45 и 7
   
2. 
   50 и 6
   
3. 
   40 и 8
   
4. 
   55 и 5
   

Решение:

1. Pmax при MR= MC

2. P = 80 – 5Q;  MR= 80 – 10Q;

3. ТC(Q)= 50 + 20Q;  MC= 20

4. Определяем объем продаж Q: MR= MC;  80 – 10Q = 20;  60 = 10Q;; Q= 6

5. Находим P (cм.п.2)= 80 – 5Q = 80 - 30= 50

А) больше капитала и меньше труда
Б) больше труда и капитала
В) меньше труда и капитала
Г) больше труда и меньше капитала

Решение:

Прибыль максимизируется при: MP_L: P_L = MP_K : P_K

Т.к. 2 : 1 > 5 : 20  необходимо уравнять неравенство, т.е. следует снизить MP_L: P_L, иными словами использовать больше труда и меньше капитала