Практика. Институт промышленных технологий и инжиниринга
 Скачать 314.16 Kb. Скачать 314.16 Kb.
|
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.Некоторые из математических возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14 версии — использует символьное ядро MuPAD. Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»). Несмотря на то, что эта программа, в основном, ориентирована на пользователей, не являющихся программистами, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования путём использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам. Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).Индивидуальное заданиеЗадача: .Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. .Определить токи во всех ветвях схемы методом контурных токов. Определить токи во всех ветвях схемы методом узловых потенциалов. .Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. Составить баланс мощности в схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Принципиальная (полная) схема: 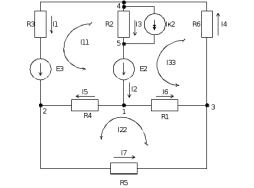 Исходные данные:
Ход работы: Рассчитаем схему по законам Кирхгофа. Произвольно зададим направления токов в ветвях и направления обхода контуров. Составим уравнения по первому закону Кирхгофа. При составлении уравнений "втекающие" в узел токи будем брать со знаком "+", а "вытекающие" - со знаком "-". Количество уравнений, составляемых по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 5 - 1 = 4. Составим уравнение для узла №1: I2-I5-I6=0 Составим уравнение для узла №2: I1+I5-I7=0 Составим уравнение для узла №3: -I4+I6+I7=0 Составим уравнение для узла №4: -I1-I3+I4-IIk2=0 Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Количество уравнений, составляемых по второму закону Кирхгофа, равно Nb – Ny + 1, где Nb - число ветвей без источников тока. Для данной схемы количество уравнений по второму закону Кирхгофа равно 7 - 5 + 1 = 3. Составим уравнение для контура №1: R3∙I1-R4∙I5-R2∙I3=E3-E2 Составим уравнение для контура №2: R4∙I5+R5∙I7+R6∙I4+R2∙I3=E2 Составим уравнение для контура №1: R4∙I5-R5∙I7-R1∙I6=0 Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом: 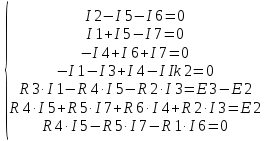 Подставим в полученную систему уравнений значения сопротивлений и источников и получим: I2-I5-I6=0 I1+I5-I7=0 -I4+I6+I7=0 -I1-I3+I4-IIk2=1.0000+0.0044j 55∙I1-100∙I5-25∙I3=-5+7.14j 100∙I5+125∙I7+25∙I4+35∙I3=84.3391.53.73j 25∙I5-75∙I7-35∙I6=0 Решим систему уравнений и получим искомые токи: I1= −0.1896+0.2444j А I2 = 0.8196+0.0730j А I3 = -0.1804+0.0687jА I4 = 0.6300+0.3174jА I5 = 0.5045-0.0228jА I6 = 0.3151+0.0958jА I7 = 0.3149+0.2216jА Проверим баланс мощностей. Определим мощность, потребляемую приёмниками: Sпр=R3⋅∣I1∣^2+R2⋅∣I3∣^2+R6⋅∣I4∣^2+R4⋅∣I5∣^2+R1⋅∣I6∣^2+R5⋅∣I7∣^2. Подставим числовые значения и получим: Sпр = 55⋅((-0.1896)^2+0.2444^2)+100⋅((-0.1804)^2+0.0687^2)+125⋅(0.6300^2+0.3174^2)+25⋅(0.5045^2+(-0.0228)^2)+75⋅(0.3151^2+0.0958^2)+35⋅(0.3149^2+0.2216^2)=90.8898. Определим мощность, отдаваемую источниками: S источника = SE+SJ где SE – мощность, отдаваемая источником ЭДС, SJ - мощность, отдаваемая источниками тока. SE= SE=E3⋅I1′+E2⋅I2′, Где I означает сопряжённый комплексный ток. Подставим числовые значения и получим: SE=(79.3353+60.8761j)⋅(−0.1896−0.2444j)+(84.3391+53.7300j)⋅(0.8196−0.0730j)=72.8811+6.9444j. Определим мощность SJ, отдаваемую источниками тока. Далее J означает сопряженный комплексный ток источника. Определим мощность SJ 2 контура, отдаваемую источником тока JIk2 Определим напряжение на источнике тока JIk2, обозначенное как UJ Для этого рассмотрим контур, проходящий через элементы JIk2, R2 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим: −UJIk2−R2⋅I3=0. UJIk2=−R2⋅I3=18.0388−6.8658j Мощность, отдаваемая источником тока JIk2: SJIk2=UJIk2⋅JIk2′=(18.0388−6.8658j)⋅(1.0000−0.0044j)=18.0087−6.9444j. Суммарная мощность, отдаваемая источниками тока, равна: SJ=SJIk2=(18.0087−6.9444j)=18.0087−6.9444j Мощность, отдаваемая источниками, равна: Sист=SE+SJ=72.8811+6.9444j+(18.0087−6.9444j)=90.8898−0j. Следовательно, Sпр = 90.8898, Sист = 90.8898−0j. Баланс мощностей сходится. Рассчитаем схему по методу узловых потенциалов. Количество уравнений, составляемых по методу узловых потенциалов, Nу−1−Ne , Nу- число узлов,Ne- число особых ветвей. Для данной схемы количество уравнений, составляемых по методу узловых потенциалов, равно 5 - 1 - 1 = 3. Так как в исходной схеме имеются особые ветви, то примем потенциал одного из узлов, к которой присоединена одна из этих ветвь, равным нулю: φ5=0В, В,тогда потенциал узла №1 равен: φ1=φ5+E2=0+(84.3391+53.7300j)=84.3391+53.7300j В. Составим уравнения для определения потенциалов остальных узлов. Уравнение для узла №2: Уравнение для узла №3: Уравнение для узла №4: Перенесём все известные слагаемые в правую часть и объединим полученные уравнения в систему. Получим: 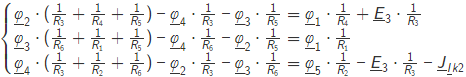 Подставим в полученную систему уравнений численные значения и получим: 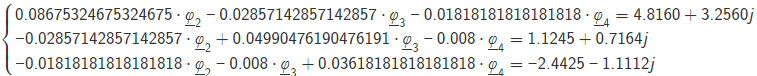 Решим систему уравнений и получим искомые потенциалы узлов: 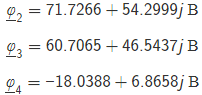 Произвольно зададим направления токов в ветвях. Определим токи во всех ветвях, кроме особых, по закону Ома для участка цепи: 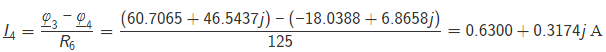 Определим по первому закону Кирхгофа токи в особых ветвях. Составим уравнения для узлов, к которым присоединены особые ветви. При составлении уравнений "втекающие" в узел токи будем брать со знаком "+", а "вытекающие" - со знаком "-". Составим уравнение для узла №1: Перенесём известные слагаемые в правую часть и получим искомый ток: Проверим баланс мощностей. Определим мощность, потребляемую приёмниками: Подставим числовые значения и получим: Определим мощность, отдаваемую источниками: где SE- мощность, отдаваемая источниками ЭДС,SJ- мощность, отдаваемая источниками тока. Определим мощность SE, отдаваемую источниками ЭДС: где I′означает сопряжённый комплексный ток. Подставим числовые значения и получим: Определим мощность SJ, отдаваемую источниками тока. Далее J′означает сопряжённый комплексный ток источника тока. Определим мощность SJIk2, отдаваемую источником тока JIk2: Определим напряжение на источнике тока JIk2, обозначенное как UJIk2. Для этого рассмотрим контур, проходящий через элементы JIk2, R2 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим: Выразим из полученного уравнения напряжение UJIk2и подставим числовые значения. Получим: Мощность, отдаваемая источником тока JIk2, равна: Суммарная мощность, отдаваемая источниками тока, равна: Мощность, отдаваемая источниками, равна: Следовательно, Sпр=90.8898, Sист=90.8898−0j. Баланс мощностей сходится. Рассчитаем схему по методу контурных токов. Количество уравнений, составляемых по методу контурных токов, равно Nв−Nу+1, где Nв - число ветвей без источников тока, Nу- число узлов. Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 7 - 5 + 1 = 3. Произвольно зададим направления обхода контуров и соответствующие контурные токи. Дополнительно зададим контурные токи, создаваемые источниками тока. Контурный ток J11 протекает через элементы J1,R2 в указанном порядке. Составим уравнения по методу контурных токов. Составим уравнение для контура №1: Составим уравнение для контура №2: Составим уравнение для контура №3: Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом: 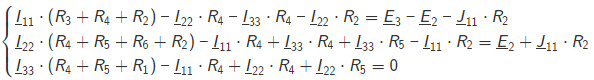 Подставим в полученную систему уравнений значения сопротивлений и источников и получим: 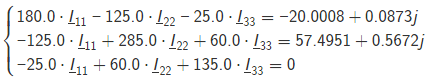 Решим систему уравнений и получим искомые контурные токи:  Произвольно зададим направления токов в ветвях. Рассчитаем токи в ветвях исходя из полученных контурных токов. Проверим баланс мощностей. Определим мощность, потребляемую приёмниками: Подставим числовые значения и получим: Определим мощность, отдаваемую источниками: Подставим числовые значения и получим: Определим мощность SJ, отдаваемую источниками тока. Далее J′означает сопряжённый комплексный ток источника тока. Определим мощность SJ1, отдаваемую источником тока J1: Определим напряжение на источнике тока J1, обозначенное как J1. Для этого рассмотрим контур, проходящий через элементы R2 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим: Выразим из полученного уравнения напряжение UJ1 и подставим числовые значения. Получим: Мощность, отдаваемая источником тока J1, равна: Суммарная мощность, отдаваемая источниками тока, равна: Мощность, отдаваемая источниками, равна: Следовательно, Sпр=9.3429, Sист=9.3429−0j. Баланс мощностей сходится. |
