средние показатели. Тема 9. Средние показатели структуры (pdf.io). Коко Шанель

Название	Коко Шанель
Анкор	средние показатели
Дата	11.04.2021
Размер	190.71 Kb.
Формат файла
Имя файла	Тема 9. Средние показатели структуры (pdf.io).docx
Тип	Документы #193451
страница	4 из 9

1 2 3 4 5 6 7 8 9

_{n 1 Me ₂_,

где n – число единиц в статистической совокупности.
(9.2)

При четном количестве единиц в совокупности медиана получается путем расчета средней арифметической из двух рядом стоящих значений признаков.

Для нахождения медианы предварительно ряд данных должен быть упорядочен. Для данных 4, 2, 1, 1, 5 упорядоченный ряд 1, 1, 2, 4, 5 будет иметь номер медианы N_ме= (5+1)/2 = 3, а медиана равна 2.

Например, в приведенном выше примере, где работники имеют стаж: 4, 2, 1, 1, 5, и 3 года, упорядоченный ряд в возрастающем (убывающем) порядке будет 1, 1, 2, 3, 4, 5 (5, 4, 3, 2, 1 и 1). Номер медианы равен N_м_е= (6+1)/2 = 3,5. Тогда медиана в первом случае равна среднему из двух значений в середине ряда (2+3) / 2 = 2,5 или во втором случае (3+2) / 2 =2,5.

В интервальном ряду распределения медиана рассчитывается по формуле (9.3):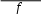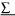

M_e^x_e^i_e²n ^Se1^,⁽⁹^.³⁾e

_г_д_еx_e_–_н_а_ч_а_ло_м_е_ди_а_н_ного_и_нт_е_рв_а_л_а_,i_e_–_д_лин_а_м_е_ди_а_н_н_о_г_о_инт_е_рв_а_л_а_,

S_e_₁_–_с_у_мм_а_н_а_копл_е_нных_ч_ас_тот_до_инт_е_рв_а_л_а_,_в_к_от_ором_н_а_ходит_сямедиана,

_f _e_{– ч}_ас_т_от_а_м_е_д_и_а_нно_г_о_инт_е_р_в_а_л_а_.

Медиана имеет свойство, благодаря которому используется в экономических расчетах (9.4):

^^|^Xi ^^М^е^|^^mⁱⁿ^,⁽⁹^.⁴⁾

В нормальных рядах распределения мода и медиана совпадают со средним арифметическим значением.

1 2 3 4 5 6 7 8 9}