Контрольная работа по информатике. КР ПО ИНФ. Контрольная работа по дисциплине Информатика и информационные технологии в профессиональной деятельности вариант 8

• Название: Контрольная работа по дисциплине Информатика и информационные технологии в профессиональной деятельности вариант 8
• Анкор: Контрольная работа по информатике
• Дата: 06.02.2022
• Размер: 1.91 Mb.
• Имя файла: КР ПО ИНФ.docx
• Тип: Контрольная работа; #353051
• страница: 2 из 5

Сложим вместе целую и дробную часть вот так:

1001100₂ + 0.10011001100₂ = 1001100.10011001100₂

Задание № 3

Изобразите логический элемент, обладающий Х=10 входами и одним выходом. Приведите таблицу истинности Вашего логического элемента. Выбор элемента выполните из условий, что N – номер варианта, причём варианты с чётными номерами используют логическую конъюнкцию, а варианты с нечётными номерами используют логическую дизъюнкцию в качестве основы логического элемента.

Решение

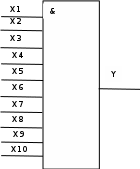
X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	Y
0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0
1	1	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0	0	0	0
0	1	1	0	0	0	0	0	0	0	0
1	1	1	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0	0	0
1	0	0	1	0	0	0	0	0	0	0
0	1	0	1	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0	0	0	0
1	0	1	1	0	0	0	0	0	0	0
0	1	1	1	0	0	0	0	0	0	0
1	1	1	1	0	0	0	0	0	0	0
0	0	0	0	1	0	0	0	0	0	0
1	0	0	0	1	0	0	0	0	0	0
0	1	0	0	1	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	0	0	1	1	0	0	0	0	0	0
1	0	0	1	1	0	0	0	0	0	0
0	1	0	1	1	0	0	0	0	0	0
0	0	1	1	1	0	0	0	0	0	0
1	0	1	1	1	0	0	0	0	0	0
0	1	1	1	1	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0
0	0	0	0	0	1	0	0	0	0	0
1	0	0	0	0	1	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	0	1	0	0	1	0	0	0	0	0
0	0	0	1	0	1	0	0	0	0	0
0	0	0	0	1	1	0	0	0	0	0
1	0	0	0	1	1	0	0	0	0	0
0	1	0	0	1	1	0	0	0	0	0
0	0	1	0	1	1	0	0	0	0	0
0	0	0	1	1	1	0	0	0	0	0
1	0	0	1	1	1	0	0	0	0	0
0	1	0	1	1	1	0	0	0	0	0
0	0	1	1	1	1	0	0	0	0	0
1	0	1	1	1	1	0	0	0	0	0
0	1	1	1	1	1	0	0	0	0	0
1	1	1	1	1	1	0	0	0	0	0
0	0	0	0	0	0	1	0	0	0	0
1	0	0	0	0	0	1	0	0	0	0