УИРС Перегинец. Корреляционный и регрессионный анализ двух зависимых выборок

• Название: Корреляционный и регрессионный анализ двух зависимых выборок
• Дата: 25.05.2022
• Размер: 36.94 Kb.
• Имя файла: УИРС Перегинец.docx
• Тип: Документы; #548420
• страница: 3 из 3

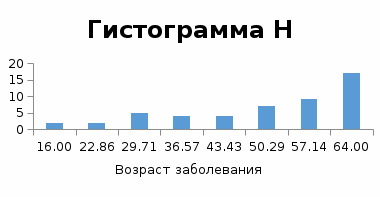𝝌э². = 7,36 𝝌кр² = 11,07

Поскольку 𝝌э² <𝝌кр² гипотеза о нормальности принимается: данные подчиняются нормальному закону распределения.

Определение коэффициента ранговой корреляции Спирмена

F	Ранг F	H	Ранг H	ri-si	(ri-si)^2	Сумма	n	Коэффициент Спирмена
Индекс массы тела (ИМТ)	ri	Возраст заболевания	si
24,58	9	23	4	5	25	2843	30	0,367519466
25,12	13	31	7	6	36
29,87	26	33	9	17	289
23,81	8	64	29,5	-21,5	462,25
24,96	11	58	22	-11	121
29,34	25	40	10,5	14,5	210,25
26,71	15	18	2,5	12,5	156,25
28,4	23	60	25,5	-2,5	6,25
25,71	14	59	23	-9	81
31,44	29	60	25,5	3,5	12,25
26,88	17	60	25,5	-8,5	72,25
31,27	28	40	10,5	17,5	306,25
23,63	7	44	13	-6	36
26,75	16	53	19	-3	9
22,45	4	18	2,5	1,5	2,25
31,15	27	62	28	-1	1
22,56	5	45	14,5	-9,5	90,25
21,47	3	26	6	-3	9
22,6	6	25	5	1	1
27,62	21	57	21	0	0
20,28	2	16	1	1	1
41,76	30	46	16	14	196
27,38	20	60	25,5	-5,5	30,25
25,01	12	45	14,5	-2,5	6,25
19,48	1	56	20	-19	361
24,69	10	42	12	-2	4
27,29	19	32	8	11	121
28,33	22	52	18	4	16
27,25	18	64	29,5	-11,5	132,25
28,99	24	50	17	7	49

∑(𝑟𝑖−𝑠𝑖)²= 2843

R(S)=0,368

Получено значение коэффициента корреляции Спирмена R(S) = 0,368. Критическое значение коэффициента Спирмена для n = 30 и уровня значимости 0,05 (таблица №5 методички) равно 0,362. Поскольку R(S)>R(крит.) найденная корреляция статистически значима.

Выводы:

1. Оба коэффициента корреляции (Пирсона и Спирмена) показывают, что корреляция средняя, положительная, статистически значима на уровне 0,05.
2. Корреляция статистически значима на уровне 0,05.