курсовая 11,2017. Курсовая работа по дисциплине Теория электрической связи Для специальности рэт
 Скачать 227.23 Kb.
|
 (3.1)Коды с обнаружением ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит помимо информационных символов - один контрольный, выбираемый равный 0 или 1 так, чтобы сумма количества единиц в комбинации всегда была четной. Простейшим примером кода с проверкой на четность является код Бодо, в котором к пятизначным комбинациям информационных символов добавляется шестой контрольный символ: 11001,1; 10001,0. Правило вычисления контрольного символа находится как:  (3.2)откуда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю. Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем случае нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы, поэтому такие ошибки не обнаруживаются. На рис. 3.1. показана структурная схема кодера. Характерной особенностью является наличие в цепи обратной связи решающее устройства, управляющего величиной шага квантования ∆b. Если знак приращений γ(k) остается неизменным в течение 3-4 интервалов дискретизации, то это означает наличие перегрузки. Решающее устройство удваивает амплитуду импульсов, поступающих на вход интегратора 1. Если в этом случае знак приращения (сигнал ошибки) не изменяется, то размер шага ∆b снова удваивается и т.д. При изменении знака приращения размер шага квантования уменьшается. Нетрудно понять, что, в состав устройства управления размером шага квантования должен входить анализатор плотности единиц и импульсный усилитель с управляемым коэффициентом усиления. На выходе интегратора 2 при изменении коэффициента усиления в зависимости от плотности единиц будет формироваться ступенчатое напряжение с адаптивно изменяющимся шагом квантования. 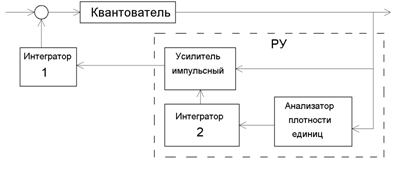 Рис. 3.1. Структурная схема кодера. Задание 4 Рассчитаем длительность единичного элемента кодовой комбинации цифрового ИКМ сигнала с проверкой на четность. Для определения длительности единичного элемента кодовой комбинации ИКМ сигнала (тактового интервала Ттакт.) с проверкой на четность последовательно определим: а) количество информационных элементов k кодовой комбинации б) общую длину кодовой комбинации n с учетом кодирования с проверкой на четность. Цифровой ИКМ сигнал - это последовательность k - разрядных кодовых комбинаций двоичного кода. Код симметричный, двоичный, где 1-й элемент кодирует знак напряжения: положительное значение напряжения - <<1>>, отрицательное - <<0>>, а последующие (k-1) элементов кодирует номер уровня квантования. Количество элементов кодовой комбинации определяется числом уровней квантования N: = ЦЧ[log2N]+1 (4.1), где ЦЧ - округлённое в большую сторону целое число. K =ЦЧ [log2512]+1=9+1=10 элементов При кодировании симметричным двоичным кодом уровни квантования нумеруются для положительных и отрицательных значений сигнала одинаково. Полярность квантованного отсчёта показывает первый элемент кодовой комбинации: положительный-<<1>> и отрицательный-<<0>>. Диапазон возможных значений аналогового сигнала: - 126 126 у.е. Шаг квантования  = 2 у.е.Описание преобразований сигнала в АЦП и в кодере проиллюстрируем примером для двух отсчетов сигнала со значениями, равными номеру варианта с положительным знаком и половине номера варианта с отрицательным знаком в условных единицах (у.е.). Для вариантов с номером меньшим чем 20, значения отсчетов взять на 20 больше, чем номер варианта. Номер варианта=07, следует Uотсч.=7+20=27(у.е.)Д1 = 27(у.е.); UКВ1 =26(у.е.); Номер уровня N = 13; Код. комбинация - 1000001101Д2 = -13,5(у.е.); UКВ2 =14(у.е.); Номер уровня N = 7; Код. комбинация - 0000000111. При кодировании помехоустойчивым (корректирующим) кодом с проверкой на четность, который позволяет обнаружить все ошибки нечётной кратности, к информационной кодовой комбинации длиной k элементов добавляется один проверочный элемент - r, доводящий число единиц в полной кодовой комбинации до чётного числа. Проверочный элемент ставится в конце кодовой комбинации после информационных элементов. Длина кодовой комбинации кода с проверкой на чётность равна: = k+1, где k - длина кодовой комбинации простого кода. Проверочный элемент определяется суммой по модулю два всех информационных элементов кодовой комбинации простого кода: r = k  k … k, где - сумма по модулю два; k , k , …k - элементы кодовой комбинации простого кода. Параметры кода: (k, k +1).У простого кода с k = 10, n = 11, параметры кода (10,11). Для кодовой комбинации 1000001101, r = 1 000001101 = 0Полная кодовая комбинация кода с проверкой на четность: 10000011010. Для кодовой комбинации 0000000111, r = 0 000000111 = 1Полная кодовая комбинация кода с проверкой на чётность: 00000001111. 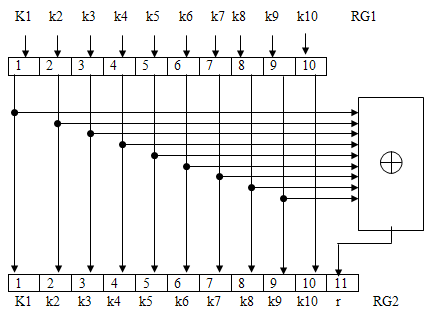 Рис. 4.1. Структурная схема кодера кода с проверкой на чётность. Общая длительность кодовой комбинации равна интервалу дискретизации Тд, определяемому по теореме Котельникова с учетом необходимого защитного частотного интервала в спектре дискретного АИМ сигнала (Fд > 2F) и кратности частоты дискретизации 8 кГц. Здесь Fд - частота дискретизации. Интервал (период) дискретизации равен: Тд =1/ FД. (4.2)  FД >23,4 = 6,8(кГц);А так как Fд должна быть кратна 8 кГц выбираем подходящую частоту FД = 8(кГц); Тд =1/ FД (4.3)Тд =1/ (8103) = 0,12510-3 (с)=12510-6(с)=125(мкс).Длительность единичного элемента кодовой комбинации цифрового ИКМ сигнала с проверкой на чётность определяется исходя из величин интервала дискретизации Fд , и длины кодовой комбинации кода с проверкой на чётность - n. Её называют тактовым интервалом - Ттакт, а частоту следования элементов - тактовой частотой - Fтакт. ТТАКТ = ТД/n,(c); (4.4)ТАКТ.=1/ТТАКТ, (Гц) (4.5)ТАКТ = n FД (Гц) (4.6) ТТАКТ = 1/FТАКТ, (c) (4.7) Вычислим ТАКТ = n FД =11 8 103 = 88 103 (Гц)=88(кГц); ТТАКТ = 1/FТАКТ = 1/(88 103) =11,36·10-6(с)=11,36(мкс). Задание 5 Определим характеристики источника независимых двоичных сообщений, если вероятность появления символа "1" р(1) = 0,001+0,kn, где k и n - предпоследняя и последняя цифры номера варианта. Вероятность появления одного из символов задается следующим образом: номер варианта=07, то вероятность появления символа "1" равна: р(1) = 0,001+0,07 = 0,071. [4, п.4.4] Необходимо последовательно рассчитать вероятность появления символа "0" - р(0), энтропию элемента - Нэл, производительность источника сообщений - Н, максимальную энтропию - Нэл.max, максимальную производительность источника -Нmax, избыточность источника сообщений - . [5, c. 200-209] Под производительностью источника двоичных сообщений понимают среднее количество информации, выдаваемое источником в единицу времени (1 сек.) - Н’. Н’ = НЭЛ / ТТАКТ, (бит/с), (5.1) Н’ = НЭЛ FТАКТ, (бит/с). (5.2) где НЭЛ - энтропия единичного элемента - среднее количество информации содержащееся в одном элементе, (бит/эл);ТАКТ - длительность единичного элемента, (с). Единичный элемент кодовой комбинации передаётся за тактовый интервал. Для источника независимых двоичных сообщений: Н ЭЛ = - [p(1) log2p(1) + p(0)log2p(0)], (бит/эл); (5.3) где p(1) и p(0) - вероятности появления символов <<1>> и <<0>>. Так как появление символов <<1>> и <<0>> составляют полную группу событий, то: р(1) + p(0) = 1, отсюда - p(0) = 1 - p(1). р(1) = 0,001+0,07 = 0,071. Следует: p(0) = 1- 0,071 = 0,929. Н ЭЛ = -[p(1) log2p(1) + p(0)log2p(0)]= -[0,071 log20,071 + 0,929 log20,929] = = -[ 0,071 (-3,813) ++ 0,929 (-0,106)] =0,369 (бит/эл.) Н’ = НЭЛ FТАКТ = 0,369 88 103 =32,47 103 (бит/c)= 32,47(кбит/c) Для двоичного кода энтропия элемента достигает максимального значения при равенстве вероятностей появления символов <<1>> и <<0>>, т.е. когда p(1) = p(0) = 0,5. Тогда: НЭЛ = НЭЛ. MAX = log2m, (бит/эл), (5.4) где m - основание кода (m=2). НЭЛ. МАХ = log22 = 1 (бит/эл.) При этом производительность источника равна: Н" = Н"МАХ = 1/ТТАКТ, = FТАКТ, (бит/c), (5.5) т.е. Н" = Н"МАХ = 1/ТТАКТ, = FТАКТ =88 103(бит/c)=88(кбит/c) Избыточность источника двоичных сообщений равна: æ = (НЭЛ.МАХ - НЭЛ)/НЭЛ.МАХ = 1 - (НЭЛ / НЭЛ. МАХ). Получим æ = 1- (0,369/1) = 0,63 Избыточность показывает долю (0,63) от максимально возможной энтропии, не используемую источником. Количество информации, содержащееся элементах <<1>> и <<0>> равно: = - log2p(1), (бит) (5.6)= -log2p(0), (бит). (5.7) Зная log2p(1)= -3,813, log2p(0)= -0,106, получим I1=3,813(бит) и I0 =0,106(бит). Количество информации в конкретной кодовой комбинации кода равно: IKK = IЭЛ 1 + IЭЛ 2 +… +IЭЛ К, или IKK = a I1 + b I0 ,(бит). (5.8) где IЭЛ I - количество информации в i- м элементе кодовой комбинации; k - количество информационных элементов в кодовой комбинации (проверочный элемент информации не несёт); а - количество элементов <<1>> в кодовой комбинации (без учёта проверочного элемента); b - количество элементов <<0>> в кодовой комбинации (без учёта проверочного элемента). IKK1 = 4 3,813 + 6 0,106 =15,89 (бит).= 3 3,813 +7 0,106 = 12,18(бит). Для увеличения энтропии источника, если p(1)  p(0), следует перекодировать кодовые комбинации ИКМ сигнала таким образом, чтобы символы нового двоичного кода были как можно более равновероятны. Это увеличит энтропию элемента (символа) нового двоичного кода. Для этой цели можно использовать неравномерный двоичный код, который содержит: две кодовые комбинации длиной в 1 элемент (k=1), т.е. 1 и 0; четыре кодовые комбинации длиной 2 элемента (k=2), т.е. 00, 01, 10, 11; восемь кодовых комбинаций длиной 3 элемента (k=3), т.е. 000, 001, 010, 011, 100, 101, 110, 111 и т.д. [5, c.200-209]Для увеличения энтропии необходимо наиболее вероятные кодовые комбинации исходного кода закодировать наиболее короткими кодовыми комбинациями нового двоичного кода (неравномерного). Так как p(1)
Задание 6 Разработаем структурную схему дискретного модулятора и алгоритм его работы. Структурная схема получения угловой модуляции в четырехполюснике с изменяющимся сдвигом фаз изображена на рисунке 6.1. Комплексный коэффициент передачи четырехполюсника:  (6.1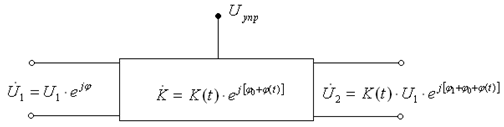)где  и  - комплексные амплитуды напряжений на входе и выходе четырехполюсника соответственно;  - модуль изменяющегося во времени коэффициента передачи четырехполюсника;  - постоянная составляющая сдвига фазы четырехполюсника;  - переменная составляющая сдвига фазы четырехполюсника. Рис 6.1 Структурная схема получения фазовой модуляции в четырехполюснике. На вход четырехполюсника от внешнего источника подается гармоническое напряжение высокой частоты, имеющие постоянную амплитуду U, и фазу  , то есть  .Комплексная амплитуда напряжения на выходе:  . (6.2)Таким образом, напряжение на выходе четырехполюсника модулировано по фазе и амплитуде. Паразитная амплитуда модуляции возникает из - за изменения модуля коэффициента передачи К(t). Паразитная амплитуда модуляции может быть уменьшена при помощи ограничителя амплитуды колебаний. В качестве четырехполюсника с переменным сдвигом фазы можно использовать, например, усилитель, резонансная частота которого изменяется при изменении индуктивности или емкости контура с помощью реактивного двухполюсника или варикапа. Для получения линейной зависимости между относительной расстройки и сдвигом фаз в пределах  , то есть индекс модуляции в одном модулированном каскаде не должен превышать П/4. При этом амплитуда выходного напряжения изменяется от 1 до 0.7.Для получения индексов модуляции, больших П/4, необходимо применить несколько последовательных каскадов с изменяющейся резонансной частотой либо умножители частоты. В диапазоне СВЧ изменение сдвига фаз осуществляется изменением электрической длины волноводов, через которые проходят модулируемые колебания. Если на вход четырехполюсника (рис. 6.1) подать закодированное сообщение (рис. 6.2, а), то на выходе получим фазомодулированные колебания (рис. 6.2, б). 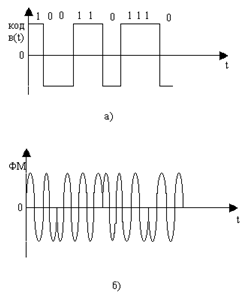 Рис 6.2. Временные диаграммы на входе - а и на выходе - б четырехполюсника. Частотно - и фазомодулированные колебания |