Оптика Лабораторные работы 1. Л. Ф. Добро, Н. М. Богатов, О. Е. Митина
 Скачать 26.45 Mb.
|
|
Контрольные вопросы к заданию 6.1
Задание 6.2. Определение постоянной дифракционной решетки Приборы и принадлежности: источник света – HeNe лазер (=6328 Å); дифракционные решетки; экран с миллиметровым масштабом; измерительная линейка. Цель задания: экспериментальное исследование распределения освещенности при дифракции света на дифракционной решетке, определение постоянной решетки. Краткая теория Дифракционной решеткой называется периодическая структура, состоящая из элементов, соизмеримых (в пределах нескольких порядков) с длиной волны. Кристаллы твердых тел представляют собой трехмерную пространственную дифракционную решетку, линейные элементы, расположенные на плоскости, могут образовать плоскую решетку, ряд точек — линейную. Прозрачные плоские дифракционные решетки изготавливаются в виде пластин из какого-либо прозрачного материла, на который алмазным резцом наносят равно отстоящие друг от друга одинаковые штрихи. Ширина прозрачного промежутка а и непрозрачного b должна быть строго постоянной для каждой решетки. Их сумма а + b = d называется постоянной, или периодом решетки. Принципиальная схема наблюдения дифракции на прозрачной решетке представлена на рис. 6.8. Пусть на дифракционную решетку 1 перпендикулярно ее плоскости падает пучок параллельных когерентных лучей. Решетка вызывает дифракцию световых лучей, и в фокальной плоскости 3 линзы 2 образуется сложное дифракционное изображение. 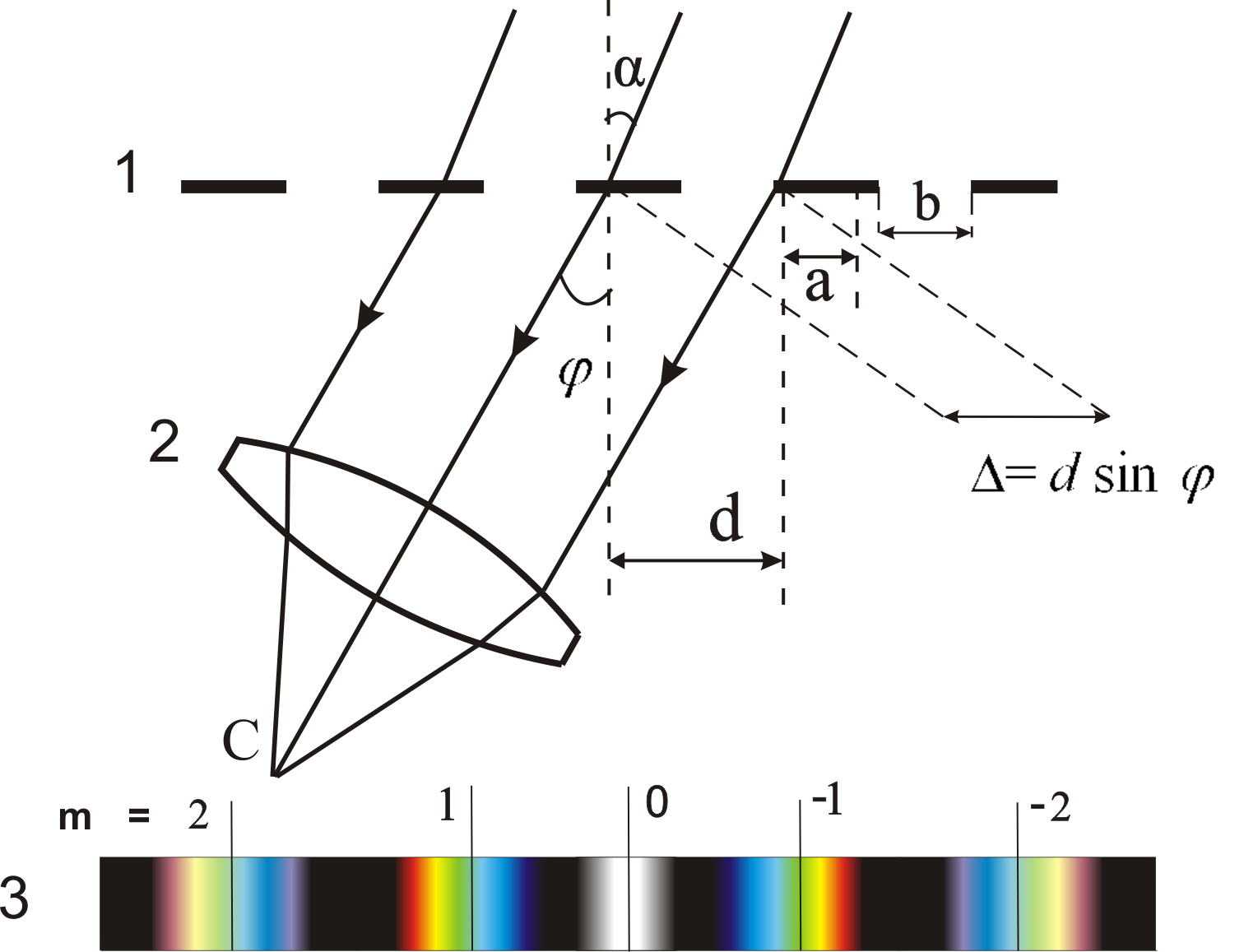 Рис. 6.8. Дифракция на дифракционной решетке Каждая щель решетки дает дифракционную картину в полном соответствии с картиной, описанной в задании 6.1. При этом дифракционные максимумы и минимумы налагаются друг на друга. Однако теперь явление усложняется тем, что кроме дифракции от каждой щели будет происходить еще интерференция многих пучков, т. е. сложение колебаний, приходящих в данную точку от всех щелей. Если общее число щелей N, то интерферируют между собой N пучков. Рассмотрим пучок параллельных лучей, дифрагировавших под углом . Амплитуды колебаний, пришедших в точку С от всех щелей, будут одинаковы, обозначим через  . Разность хода между лучами от каждой из двух соседних щелей, как видно из рис.6.7, равна = (а + b) sin = d sin . (6.4) Этой разности хода соответствует разность фаз между соседними лучами от каждых двух соседних щелей, равная  . (6.5)Суммарную амплитуду можно представить графически вектором замыкающей ломаной линии, образованной векторами амплитуд . Очевидно, что вектор  достигает максимальной величины во всех случаях, когда векторы расположены вдоль одной прямой (рис. 6.4, а). Это имеет место при = ± 2k, где k = 0,1,2… При этом длина вектора равна сумме векторов амплитуд от всех щелей  . Освещенность прямо пропорциональна квадрату амплитуды. Следовательно, максимальная освещенность Imaxбудет равнаImax = CN2a2 , (6.6) где C коэффициент пропорциональности. Максимумы, соответствующие условию (6.6), называются главными. Вектор становится равным 0, когда ломаная линия, образованная векторами , превращается в замкнутую линию (рис. 6.4, б), т. е. когда последний вектор  направлен так же, как  , но последний составляет с осью ОХ угол N . Следовательно, вектор будет параллелен оси ОХ при N = ± 2k, где k = 1, 2, 3 …Таким образом, получаем условие образования минимумов  . (6.7)В минимумах освещенность Imin = 0. Нетрудно видеть, что между максимумами имеется N–1 минимум, а следовательно, еще N–2 максимума. Эти максимумы очень слабые и называются вторичными максимумами. Приняв во внимание соотношение (6.4) и (6.5), получим, что главные максимумы возникают при значениях угла , удовлетворяющих условию d sin = k; k = 0,1,2. (6.8) 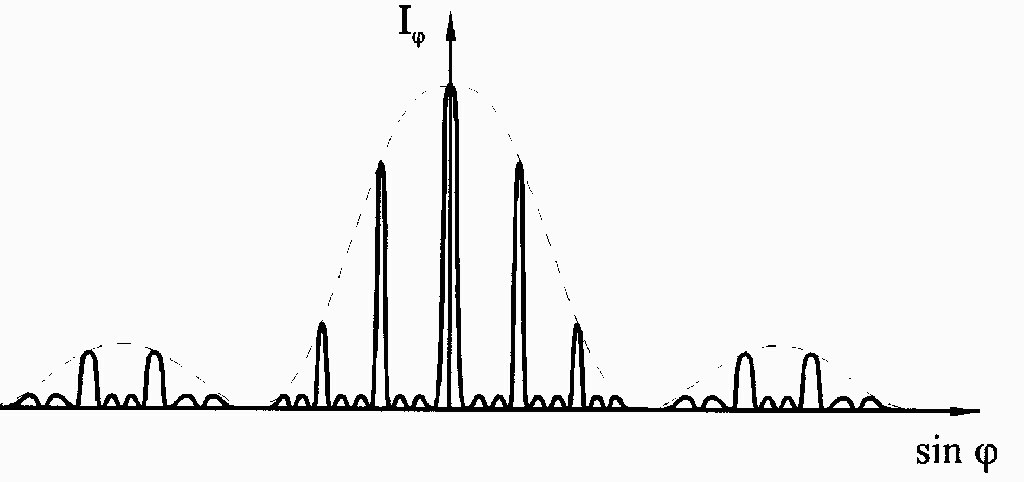 Рис. 6.9. Распределение освещенности при дифракции на дифракционной решетке состоящей из четырех щелей Целое число k называют порядком спектра, выражение (6.8) формулой дифракционной решетки. Минимумы возникают при значениях , удовлетворяющих условию  k = 1,2,3… , (6.9)кроме k= N, 2N, 3N... Учитывая дифракцию от каждой щели и описанную ранее интерференцию от N щелей решетки, освещенность I в фокальной плоскости линзы 3 (рис. 6.8) получим в виде произведения I = I1I2, где I1 освещенность, обусловленная дифракцией на каждой щели, I2 – освещенность, обусловленная интерференцией на решетке. На рис. 6.7 представлено истинное распределение освещенности при дифракции от четырех щелей. Если на дифракционную решетку падает не монохроматический пучок лучей, то условия максимумов (6.7) и минимумов (6.9) будут справедливы для всех длин волн и в фокальной плоскости 3 линзы 2 (рис. 6.7) будет наблюдаться дифракционный спектр в виде смещенных максимумов для всех длин волн источника света. Как показывает формула (6.8), в центре будет максимум нулевого порядка для всех длин волн 1, 2,…, n . По обе стороны от этого максимума будут располагаться максимумы 1-го, 2-го и т.д. порядков, соответственно для всех длин волн 1, 2,…; при этом, чем короче длина волны, тем ближе расположен соответствующий максимум к центральному. Эта картина будет дифракционным изображением, полученным в результате ограничения светового пучка дифракционной решеткой. Следовательно, дифракционная решетка – прибор, разлагающий белый свет на составные части, с ее помощью получается дифракционный спектр. Формула (6.8) позволяет определить длину волны , если известна постоянная решетки d и порядок максимума k. В более общем случае, когда решетка освещается немонохроматическим (сложным, например, белым) светом, дифракционная картина усложняется (рис. 6.10). 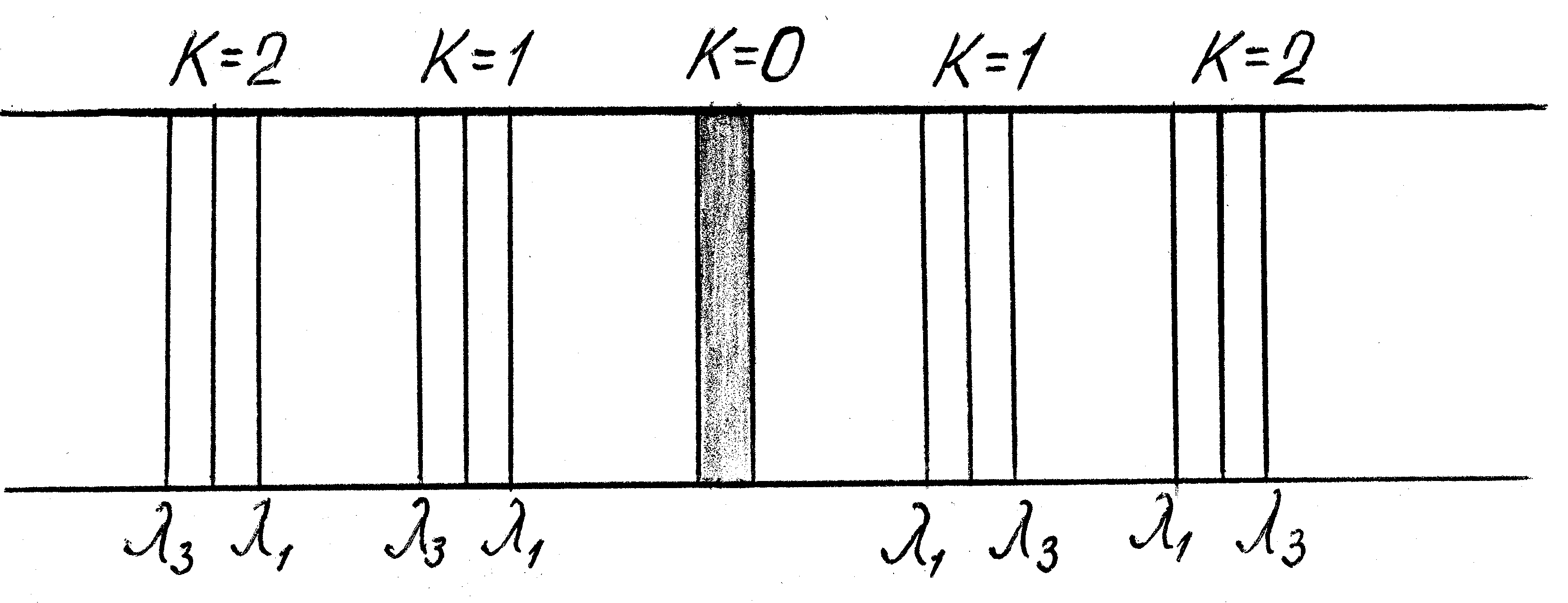 Рис. 6.10. Схематический вид дифракционного спектра При k = 0 условие максимумов, удовлетворяется для всех длин волн, т.е. при = 0 наблюдается центральная световая полоса, соответствующая неотклоненному пучку лучей такого цвета, каким был цвет источника. При k = 1 симметрично по обе стороны от центральной полосы получаются дифракционные цветовые линии, от фиолетового до красного, соответствующие разным длинам волн, входящим в состав смешанного цвета. Эта группа линий называется спектрами 1-го порядка. Красная часть спектра отклонена больше, чем фиолетовая. При k = 2 получают аналогичные спектры 2-го порядка. Линии спектров высоких порядков менее интенсивны, и на практике ясно наблюдаются спектры не выше 3-го порядка. Рассмотрим один из методов определения длины волны при помощи дифракционной решетки. Освещая дифракционную решетку 2 (рис. 6.10) с помощью лазера 1 на расположенном за ней экране 3, можно получить четкую дифракционную картину без использования фокусирующей линзы. Так как в установке используется монохроматическое лазерное излучение, то дифракционная картина будет представлять собой ряд ярких симметрично расположенных пятен (максимумов), интенсивность которых убывает при смещении влево и вправо от центра дифракционной картины. 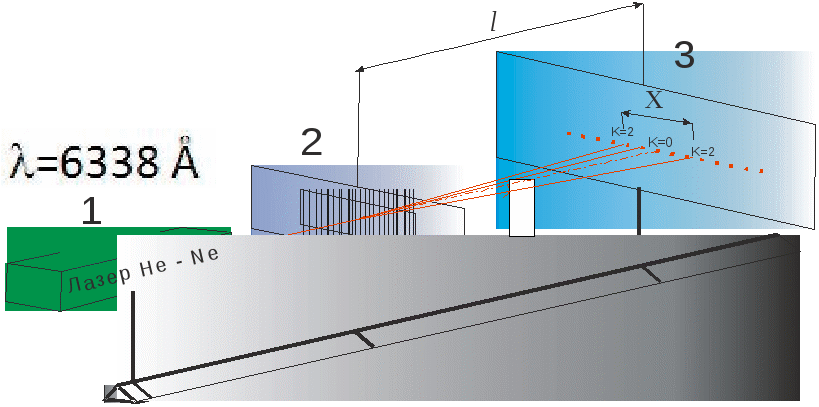 Рис. 6.10. Схема установки для определения постоянной дифракционной решетки: 1 – лазер; 2 – дифракционная решетка; 3 экран; l расстояние от решетки до экрана; х расстояние между центрами максимумов одноименных порядков Для определения длины волны по формуле (6.8) необходимо знать sin . Так как l>> х, то sin tg =  .Подставляя значения в выражение (6.8), получим окончательную формулу для нахождения длины волны  . (6.10)Длина волны измеряется в микрометрах (1 мк = 10–6 м), нанометрах (1 нм =10-9 м) или ангстремах (1 Å = 10–10 м). В данном задании необходимо вычислить постоянную дифракционной решетки, выразив ее из формулы (6.10),  (6.11)и рассчитать число штрихов на 1 мм:  , (6.12)значение N выражается в мм–1. Для измерений используют две дифракционные решетки. Порядок выполнения работы задания № 6.2
Таблица 6.2
Контрольные вопросы к заданию 6.2
Рекомендуемая литература: [1], [4], [11], [12], [14]. Лабораторная работа 7 ИССЛЕДОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ Задание 7.1. Определение фокусного расстояния собирающей линзы методом Бесселя Приборы и принадлежности: экран, линза, осветитель, оптическая скамья и рейтеры, линейка Цель задания: экспериментальное определение фокусного расстояния собирающей линзы методом Бесселя. Краткая теория Линзой называется прозрачное тело (обычно из стекла), ограниченное двумя сферическими поверхностями. Одна из поверхностей линзы может быть плоской (т.е. иметь бесконечно большой радиус кривизны). Линза простейший частный случай центрированной оптической системы и обладает всеми ее свойствами. В теории Гаусса описывается идеальная оптическая система, т.е. система, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету. Это есть чисто геометрическая теория, устанавливающая соотношения между точками, линиями и плоскостями в пространстве предметов и пространстве изображений. Прямая, соединяющая центры сферических поверхностей точки О1 и О2 (рис. 7.1), представляет собой ось симметрии центрированной системы и называется ее главной оптической осью. Теория Гаусса устанавливает шесть так называемых кардинальных точек одномерных кардинальных плоскостей, задание которых полностью определяет все свойства оптической системы. Учитывая, что кардинальные точки не являются линейно независимыми для описания центрированной системы (в том числе и для построения изображений), оказывается достаточным задание четырех из них. 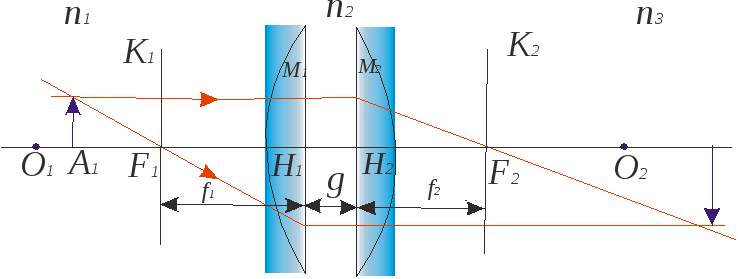 Рис. 7.1. Центрированная оптическая система: F1 , F2 – передний и задний фокусы; K1F1, K2F2 – передняя и задняя главные точки системы; M1H1, M2H2 – передняя и задняя главные плоскости Точки F1 и F2 называются передним и задним фокусом системы, если сопряженные с ними точки находятся в бесконечности. Следовательно, в фокусах F1 и F2 пересекаются лучи, падающие на оптическую систему (соответственно справа и слева) параллельно ее главной оптической оси. Фокусы F1 и F2 являются кардинальными точками системы, а проходящие через них перпендикулярно главной оптической плоскости – кардинальными фокальными плоскостями системы. Две перпендикулярные главной оптической оси плоскости М1Н1 и М2Н2, точки которых сопряжены и изображаются с увеличением, равным +1 (т. е. плоскость М1Н2изображается на М2Н2 прямо, в натуральную величину), называются главными плоскостями системы, а точки пересечения этих плоскостей с главной оптической осью – главными точками. Главные плоскости и главные точки также кардинальные элементы системы. Передним фокусным расстоянием системы называется расстояние F1 = F1H1, т. е. расстояние от переднего фокуса до передней главной точки, аналогично задним фокусом называется расстояние F2 = H2F2 . Можно показать, что если показатели преломления пространства предметов n1 и пространства изображений n3 равны (n1 = n3) , то переднее и заднее фокусные расстояния системы также равны (F1 = F2). На рис. 7.1 дан возможный вариант построения изображения A2B2 предмета A1B1 с учетом свойств, рассмотренных кардинальных элементов системы. В зависимости от вида ограничивающих поверхностей линзы бывают двояковыпуклыми, плосковыпуклыми, двояковогнутыми, плосковогнутыми и вогнуто-выпуклыми. На рис. 7.2 изображены различные типы линз и их главные плоскости. 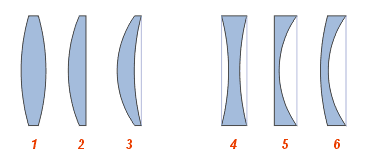 Рис. 7.2. Типичные линзы с указанием их главных плоскостей: собирающие: 1 — двояковыпуклая, 2 — плоско выпуклая, 3 — вогнуто-выпуклая (положительный (выпуклый) мениск); рассеивающие: 4 — двояковогнутая, 5 — плоско вогнутая, 6 — выпукло-вогнутая (отрицательный (вогнутый) мениск); Как видно из рис. 7.2, главные плоскости (главные точки) могут лежать как внутри, так и вне линзы совершенно несимметрично относительно ее поверхностей. Если толщина линзы достаточно мала по сравнению с радиусами кривизны ограничивающих ее поверхностей и можно считать, что передняя и задняя главные плоскости, передняя и задняя поверхности пересекают главную оптическую ось в одной общей точке, то линзу называют тонкой, а точку пересечения слившихся плоскостей с главной оптической осью – оптическим центром линзы. В этом случае переднее и заднее фокусные расстояния линзы отсчитываются от ее оптического центра. Рассмотрим тонкую собирающую линзу (рис. 7.3). Будем предполагать, что n1 = n3 = 1; n2 = n; F1 = F2 = F. Конкретизируем сформулированные ранее свойства оптической системы применительно к этому частному случаю. На рис. 7.3 оптический центр это точка О, проходя через которую лучи не изменяют направления. Всякая прямая, проходящая через оптический центр, называется оптической осью, и если она, кроме того, проходит через центры кривизны (O1 и O2) – главной оптической осью. Плоскость, перпендикулярная главной оптической оси и проходящая через оптический центр, называется главной плоскостью линзы. 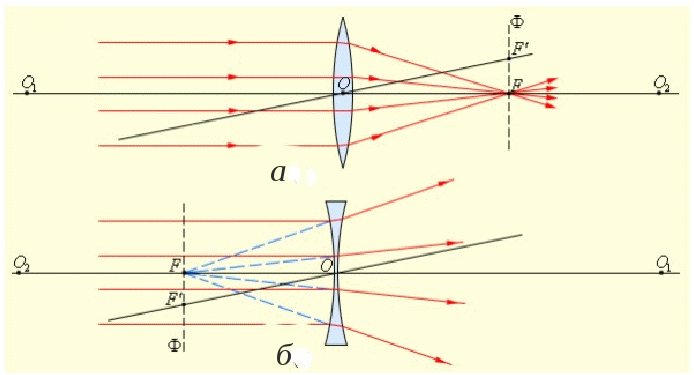 Рис. 7.3. Преломление параллельного пучка лучей: а – в собирающей; б – рассеивающей линзах. Точки O1 и O2 – центры сферических поверхностей; O1O2 – главная оптическая ось, O – оптический центр, F – главный фокус; F' – побочный фокус, OF' – побочная оптическая ось;Ф – фокальная плоскость Главным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, падающие на нее пучком, параллельным главной оптической оси (на рис. 7.3 точки F). Расстояние главного фокуса от оптического центра линзы (расстояние ОF1 и ОF2) называется главным фокусным расстоянием и является основной характеристикой линзы. Для собирающих линз главное фокусное расстояние – величина положительная, для рассеивающих – отрицательная. Часто линзу характеризуют оптической силой D = 1/F– величиной, обратной главному фокусному расстоянию, выраженному в метрах (если линза находится в среде с показателем преломления, отличным от 1, оптическая сила линзы D = n / F, где n – показатель преломления среды). Для рассеивающих линз главный фокус мнимый, для его отыскания берут не сами лучи, а их продолжение (рис. 7.1). Для построения изображения предмета с помощью линзы пользуются лучами, ход которых через линзу известен. Обычно берут два луча из следующих трёх: 1 проходит через оптический центр (идёт через линзу не преломляясь); 2 – падает на линзу параллельно её главной оптической оси (при выходе из линзы пройдет через её главный фокус); 3 проходит через главный фокус линзы (он из линзы выйдет параллельно её главной оптической оси) (рис. 7.4). 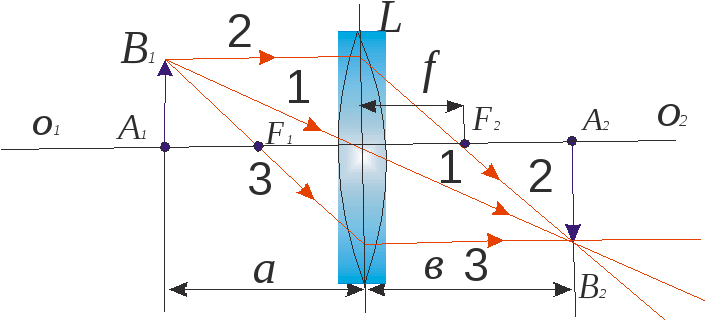 Рис. 7.4. Лучи, используемые для построения изображений в линзах Изображение предмета AB в зависимости от того, на каком расстоянии от линзы он будет находиться, может получиться увеличенным или уменьшенным, действительным (как на рисунке) или мнимым. Делая построение изображения, мы ограничились лучами, образующими малые углы с оптической осью линзы (параксиальные лучи). Обозначим через a (рис. 7.4) расстояние от предмета до линзы, а через в – расстояние от линзы до изображения. Зависимость между a, в и F (фокусным расстоянием) даёт нам формулу тонкой линзы  (7.1) Линейное увеличение, даваемое тонкой линзой, равно  (7.2)т. е. линейным увеличением называется отношение размера изображения предмета к соответствующему размеру предмета. О  птическая сила тонкой линзы может быть рассчитана по формуле (7.3) где F– фокусное расстояние линзы; R1 и R2 – радиусы кривизны первой и второй преломляющих поверхностей линзы, считаемые по ходу луча света; n – показатель преломления материала линзы. Радиусы выпуклых поверхностей считаются положительными, вогнутых – отрицательными. При определении фокусного расстояния собирающей линзы обычно применяют формулу тонкой линзы. Однако положение оптического центра линзы не всегда известно, поэтому расстояние f находят не непосредственно, а используя метод перемещения линзы – метод Бесселя. Определение фокусного расстояния собирающей линзы по методу ее перемещения сводится к следующему. Если расстояние от предмета до изображения больше 4f, то всегда найдутся два таких положения линзы, при которых на экране получается отчетливое изображение предмета: в одном случае увеличенное, в другом – уменьшенное (рис. 7.5). 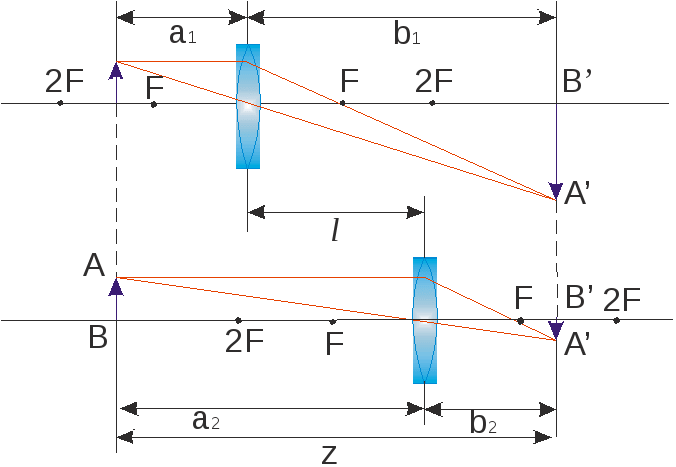 Рис. 7.5. Схема измерения фокусного расстояния линзы по методу Бесселя Для одного положения линзы расстояние от предмета до линзы и от линзы до изображения обозначим через a1 и b1, а для другого – a2 и b2. Так как расстояние между экраном и предметом остаётся неизменным, то a1+b1=a2+b2. Из этого равенства и равенства 1/F= (a+b)/(ab), которое представляет собой преобразованную формулу тонкой линзы, заключаем, что совместное существование указанных формул возможно только в том случае, когда a1=b2 и a2=b1. Обозначив расстояние между обоими положениями линзы через l, получим   Подставляя эти значения в формулу линзы и решая относительно главного фокусного расстояния, получим  ; (7.4)Формула (7.4) носит название формулы Бесселя. Если рассматривать реальную толстую линзу, то главные ее плоскости не будут совпадать, образуя оптический центр линзы. Метод Бесселя применим и в этом случае. Формула для вычисления фокусного расстояния, помимо введенных ранее величин z и l, будет содержать величину g – расстояние между главными плоскостями линзы (см. рис. 7.1) (  7.5)Для расчета фокусного расстояния F по формуле (7.5) необходимо знать величину g. Для ее определения можно повторить опыт, взяв другое расстояние z1 между предметом (спиралью лампы) и экраном: 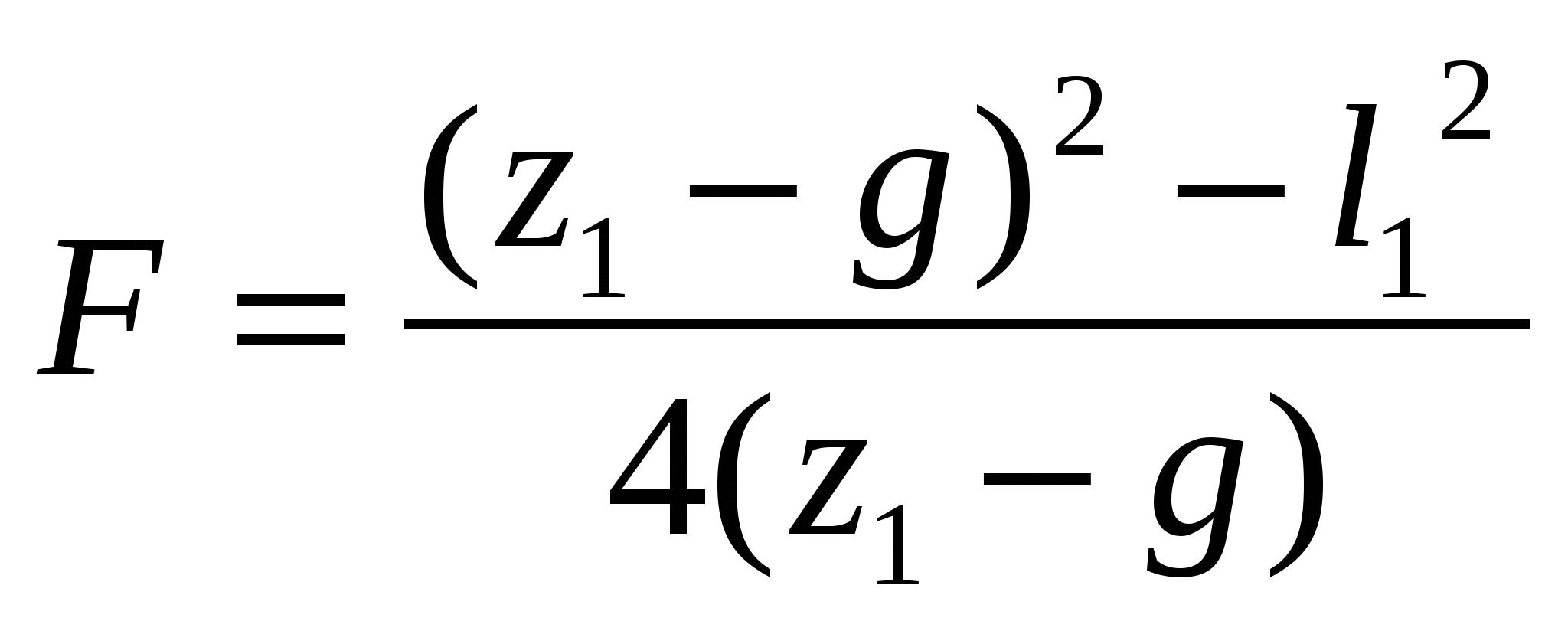 . (7.6) Решая совместно уравнения (7.5) и (7.6), можно определить F и g. Для упрощения расчета в последних формулах можно пренебречь g2 по сравнению с z2, тогда для расчета фокусного расстояния линзы получим выражение  (7.7) Порядок выполнения задания 7.1 1. Расположить приборы на оптической скамье, как показано на рис. 7.6. 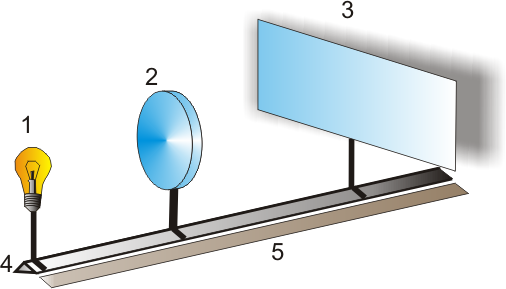 Рис. 7.6. Схема экспериментальной установки: 1 – экран; 2 линза; 3 – предмет (спираль лампы); 4 – оптическая скамья; 5 – линейка 2. Передвигая линзу, добиться получения на экране отчётливого изображения предмета – спирали лампы, например, увеличенного. Отмечать на оптической скамье положение линзы l1. Не изменяя положения экрана и осветителя, перемещая только линзу, получить на экране уменьшенное изображение спирали. Вновь отметить положение линзы на скамье l2. Положение линзы удобно отмечать, засекая, например, положение переднего края рейтера, на котором установлена линза. 3. Опредить расстояние l между двумя положениями линзы, l= |l2 – l1|. 4. Измерить расстояние z между предметом и экраном. 5. Опыт повторить несколько раз, изменяя расстояние между предметом и экраном. Проводить расчет фокусного расстояния по формуле (7.4). 6. Используя данные измерений любых двух опытов, проводить расчет фокусного расстояния F и расстояния между главными плоскостями g по формулам (7.5)–(7.7). Данные занести в табл.7.1. Таблица 7.1
7. Оценить случайные и систематические погрешности измерений. Линза, используемая в лабораторной работе, состоит из двух плосковыпуклых одинаковых линз, сложенных вместе плоскими сторонами и укреплённых в одной оправе. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||