Пример 1. Бригада рабочих выполняет комплекс из 13 работ, для каждой из которых известна продолжительность, а также то, на какие работы комплекса она опирается (табл. 8.1). Требуется построить и рассчитать сетевую модель, найти критический путь.
Для того чтобы узнать порядок построения работ и событий, определим ранги всех работ. К работам первого ранга относим те, которые не опираются ни на какие другие работы. В нашем примере это работы Д, Е, Ж и З (табл. 8.2).
Таблица 8.1
Исходные данные
Индекс работы
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
И
|
К
|
Л
|
М
|
Н
|
Продолжительность работы, ч
|
4
|
3
|
2
|
5
|
3
|
4
|
2
|
2
|
4
|
2
|
10
|
3
|
3
|
Работы, на которые опирается данная работа
|
К
|
Г, В
|
Н
|
З
|
–
|
–
|
–
|
–
|
Д, Ж
|
М, Л
|
Е
|
Н
|
И, Ж
|
Таблица 8.2
Определение работ первого ранга
Индекс работы
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
И
|
К
|
Л
|
М
|
Н
|
Работы, на которые опирается данная работа
|
К
|
Г, В
|
Н
|
З
|
–
|
–
|
–
|
–
|
Д, Ж
|
М, Л
|
Е
|
Н
|
И, Ж
|
Ранг работы
|
|
|
|
|
1
|
1
|
1
|
1
|
|
|
|
|
|
Затем выявляем работы второго ранга (табл. 8.3), которые опираются хотя бы на одну работу первого ранга. Это Г (опирается на З), И (опирается на Д, Ж), Л (опирается на Е), Н (опирается на Ж):
Таблица 8.3
Определение работ второго ранга
Индекс работы
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
И
|
К
|
Л
|
М
|
Н
|
Работы, на которые опирается данная работа
|
К
|
Г, В
|
Н
|
З
|
–
|
–
|
–
|
–
|
Д, Ж
|
М, Л
|
Е
|
Н
|
И, Ж
|
Ранг работы
|
|
|
|
2
|
1
|
1
|
1
|
1
|
2
|
|
2
|
|
2
|
К работам третьего ранга относим работы, опирающиеся хотя бы на одну из выявленных работ второго ранга (Г, И, Л, Н). Это Б (опирается на Г), В (опирается на Н), К (опирается на Л), М (опирается на Н).
И, наконец, работе А присваиваем четвертый ранг, так как она опирается на работу третьего ранга К (табл. 8.4).
Построение сетевой модели (рис. 8.3) начинаем с построения оси времени. Над временной осью вычерчиваем события и работы. Начинаем с исходного события, которое обозначаем кружком, расположенным напротив нулевой отметки временной оси. Индекс исходного события – О. Затем строим работы первого ранга (Д, Е, Ж и З). Поскольку они являются действительными (так как имеют определенную, указанную в условии задачи продолжительность), то изображаются сплошными стрелками, которые выходят из исходного события, и заканчиваются событиями, символизирующими окончание данных работ.
Индексы событий соответствуют индексам работ, завершением которых они являются. Кружки событий располагаются на произвольной высоте, но строго напротив координаты временной оси, соответствующей времени совершения события. Так, например, работа Е имеет продолжительность 4 ч. Это означает, что кружок завершение работы Е должен располагаться над отметкой 4 по оси времени. Продолжительность работ указывается над соответствующими работами стрелками.
Таблица 8.4
Определение работ третьего и четвертого рангов
Индекс работы
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
И
|
К
|
Л
|
М
|
Н
|
Работы, на которые данная работа опирается
|
К
|
Г, В
|
Н
|
З
|
–
|
–
|
–
|
–
|
Д, Ж
|
М, Л
|
Е
|
Н
|
И, Ж
|
Ранг работы
|
4
|
3
|
3
|
2
|
1
|
1
|
1
|
1
|
2
|
3
|
2
|
3
|
2
| 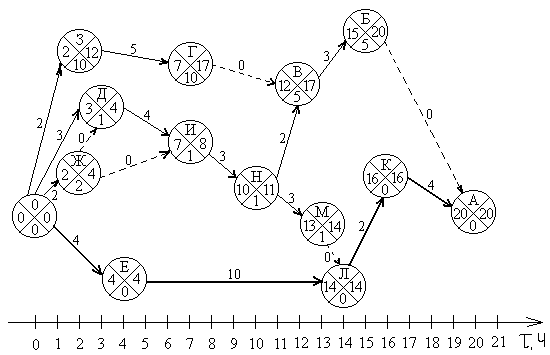 Рис. 8.3. Сетевая модель
После построения всех работ первого ранга начинают построение работ второго ранга (Г, И, Л, Н). Работа Г опирается на работу З, поэтому ее стрелка выходит из события З, а срок выполнения работы Г складывается из срока выполнения З и собственно Г (2 + 5 = 7). Событие завершения Г располагается над координатой времени 7.
Работа И опирается на две работы: Д и Ж. Другими словами, она не может начаться раньше, чем закончатся Д и Ж. Однако работа Д заканчивается позже (в 3 ч), чем Ж (2 ч). Значит, И может начинаться только после окончания Д. Таким образом, стрелка работы И выходит из события Д (как более позднего из Д и Ж), а логическая связь, существующая между работами Д и Ж, изображается стрелкой фиктивной работы с нулевой продолжительностью. Данную логическую связь можно сформулировать, например, таким образом: бригада рабочих, выполнявших работу Ж, в течение часа отдыхает (совершает фиктивную работу), ожидая, когда освободятся рабочие, выполняющие работу Д, а затем обе бригады вместе приступают к выполнению работы И.
Работа Н также является работой второго ранга, но не может быть построена раньше, чем Ж и И, на которые она опирается. И только после того как вычерчены события Ж и И, из них выбирается то, которое заканчивается позднее (И), и от него строится стрелка работы Н. Вновь необходимо соединить фиктивной работой события Ж и И.
Построение сетевой модели продолжается до построения события завершения последней работы А, т. е. до построения завершающего события. После того как все работы и события построены, нужно проверить, нет ли обрывов в путях модели. Все события, кроме исходного и завершающего, являются одновременно точкой завершения одних работ и начала других. Исключением является событие Б, из которого не выходит ни одна стрелка, а значит цепь на данном событии обрывается. Такого быть не должно, поэтому вводим фиктивную работу, соединяющую событие Б с завершающим событием А. Данная логическая связь выражает следующее: комплекс работ не может быть завершен, пока не завершена хотя бы одна работа комплекса.
Теперь можно приступать к расчету модели. Сначала в левом секторе каждого события проставляют ранний срок его наступления, который соответствует координате события по оси времени. Затем в правом секторе завершающего события А проставляют поздний срок, который равен раннему.
Поздний срок события К равен разности позднего срока события А и продолжительности работы А: tКп = 20 – 4 = 16.
Поздний срок события Л равен разности позднего срока события К и продолжительности работы Л: tЛп = 16 – 2 = 14.
Поздний срок события М равен разности позднего срока события Л и продолжительности фиктивной работы: tМп = 14 – 0 = 14.
Поздний срок события Б равен разности позднего срока события А и продолжительности фиктивной работы: tБп = 20 – 0 = 20.
Поздний срок события В равен разности позднего срока события Б и продолжительности работы Б: tВп = 20 – 3 = 17.
Поздний срок события Н может быть рассчитан как
tНп = 17 – 2 = 6 или tНп = 14 – 3 = 11. В правилах расчета сетевой модели сказано, что в качестве позднего срока любого события выбирается минимальный из всех возможных. Поэтому принимаем tНп = 11.
Анализ результата расчета сетевой модели позволяет сделать следующие выводы:
критический путь модели проходит через события Е, Л, К и А. Это означает, что любые задержки в выполнении данных работ приведут к увеличению срока выполнения комплекса работ в целом;
минимальная возможная продолжительность выполнения всего комплекса работ составляет 20 ч;
увеличение продолжительности выполнения работ З, Г, Б, В, М, Н, И, Ж, Д на время, равное резерву, не приведет к срыву графика сдачи комплекса работ.
Пример 2. Рассмотрим технологический процесс изготовления крышки стола из ДСтП, облицованной натуральным шпоном. Пусть имеется список операций, которые включает в себя данный технологический процесс (табл. 8.5). Требуется построить сетевую модель данного технологического процесса и определить минимальную продолжительность изготовления готового изделия.
Таблица 8.5
Исходные данные
Операция
|
Продолжительность операции, с
|
Облицовывание пласти плиты
|
65
|
Облицовывание кромок плиты
|
25
|
Снятие свесов
|
20
|
Прирубка шпона
|
10
|
Ребросклеивание шпона
|
10
|
Приготовление клея
|
35
|
Упрочнение торцов облицовочного материала
|
15
|
Окончание табл. 8.5
Операция
|
Продолжительность операции, с
|
Шлифование
|
20
|
Нанесение лакокрасочного материала
|
40
|
Раскрой плиты
|
70
|
Доставка на участок облицовывания
|
30
|
Для удобства каждой операции присвоим индекс. Определим, на какие операции опирается каждая из них. Результаты занесем в табл. 8.6.
Таблица 8.6
Индексирование операций
Операция
|
Продолжительность операции, с
|
Индекс операции
|
На какие операции опирается данная операция
|
Облицовывание пласти плиты
|
65
|
А
|
Е, К
|
Облицовывание кромок плиты
|
25
|
Б
|
В
|
Снятие свесов
|
20
|
В
|
А
|
Прирубка шпона
|
10
|
Г
|
-
|
Ребросклеивание шпона
|
10
|
Д
|
Г
|
Нанесение клея
|
10
|
Е
|
Ж
|
Упрочнение торцов облицовочного материала
|
15
|
Ж
|
Д
|
Шлифование
|
20
|
З
|
Б
|
Нанесение лакокрасочного материала
|
40
|
И
|
З
|
Раскрой плиты
|
100
|
К
|
-
|
Сетевая модель технологического процесса показана на рис. 8.4.
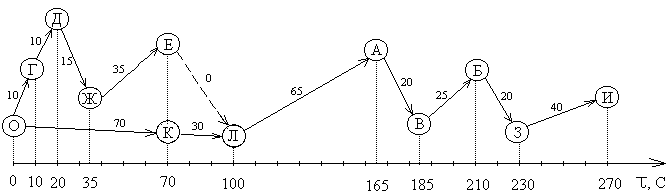 Рис. 8.4. Сетевая модель технологического процесса
Минимальная продолжительность технологического процесса составляет 270 с.
|
 Скачать 229 Kb.
Скачать 229 Kb.

