Лабораторная работа по курсу общей физики ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. МАЯТНИК ОБЕРБЕКА. Лаба 2. Лабораторная работа по курсу общей физики динамика вращательного движения. Маятник обербека преподаватель Студенты гр. 1А0
 Скачать 82.52 Kb. Скачать 82.52 Kb.
|
|
Министерство науки и высшего образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждения высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра Физики ОТЧЕТ Лабораторная работа по курсу общей физики ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. МАЯТНИК ОБЕРБЕКА Преподаватель Студенты гр. 1А0 ____________ Е.В. Палешева ____________ Е. Тарасов «12» октября 2020 г. ____________ С. Небратов «12» октября 2020 г. 2020 ВВЕДЕНИЕ Целью данной лабораторной работы является экспериментальное исследование зависимости углового ускорения от конструктивных параметров маятника, а именно: от момента инерции Iпривесок. Установление такой связи позволяет косвенно проверить основные законы динамики поступательного и вращательного движений. ОПИСАНИЕ ЭКСПЕРЕМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЙ Экспериментальная установка представляет собой крестообразный маятник (маятник Обербека), схематически изображенный на рисунке 1.1 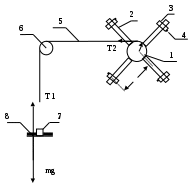 1 – Барабан, 2 – Стержень, 3 – Привеска, 4 – Стопорной винт, 5 – Нить, 6 – Блок, 7 – Грузик, 8 – Чашечка Рисунок 1.1 – Схема экспериментальной установки Методика измерений заключается в следующем. Устанавливаются все 4 привески на минимальном расстоянии от оси барабана и фиксируются винтами. При вращении маховика, поднимается груз, чье положение запоминается для того, чтобы в каждом опыте начальная точка движения груза было одной и той же. Измеряется время (t) падения груза на пол. После измерения все привески вдоль стержней смещаются на несколько сантиметров дальше от оси вращения (на одинаковые расстояния). Исследование повторяется до тех пор, пока привески не окажутся на концах. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Формула нахождения момента силы трения в подшипниках барабана:  (2.1) 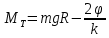 где φ – угол поворота, R – радиус барабана, k – угловой коэффициент, m — масса груза Формула нахождения момента инерции ненагруженного маятника:  (2.2) 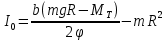 где MT – момент силы трения в подшипниках барабана, b – свободный член, m – масса груза, R – радиус барабана Формула нахождения суммарного момента инерции привесок:  (2.3) 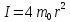 где m0 — масса одной привески, r – расстояние от оси вращения маятника до центра привески Формула нахождения случайной погрешности и доверительного интервала:  (2.4) σ( 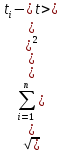  (2.5) Δ = 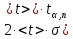 , , где 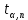 – коэффициент Стьюдента – коэффициент СтьюдентаРЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ Таблица 3.1 – Результаты зависимости времени падения груза от момента инерции привесок
Используя данные из таблицы (3.1), по формулам (2.4) и (2.5) рассчитываем случайную погрешность и доверительный интервал: Δ1 = 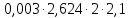 = 0,03 = 0,03Δ2 = 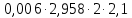 = 0,07 = 0,07Δ3 = 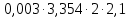 = 0,04 = 0,04Δ4 = 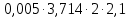 = 0,07 = 0,07Δ5 = 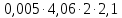 = 0,08 = 0,08Δ6 = 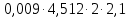 = 0,17 = 0,17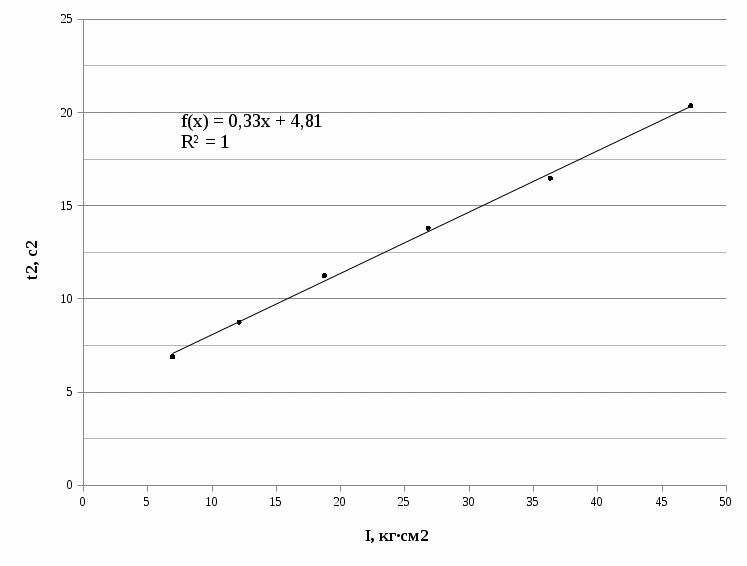 Рисунок 3.1 – Зависимость квадрата времени падения груза от момента инерции привесок Из графика определяем коэффициент k и свободный член b, которые равны:k= 0,329, b=4,81 Используя формулу (2.1) находим момент сил трения в подшипниках барабана: MT = 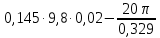 = – 190,95 Н = – 190,95 Н м мПо формуле (2.2) находим момент инерции ненагруженного маятника: I0 = 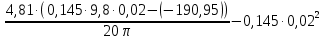 = 14,62 кг = 14,62 кг м2 м2ЗАКЛЮЧЕНИЕ График, построенный на основании обработанных данных экспериментальных измерений доказал, что квадрат времени линейно зависит от момента инерции, также момент инерции зависит от конструктивных параметров маятника: от момента инерции привесок. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

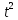 ,
,