Базы данных. Лекции БД. Лекция 5 Основные понятия информационных систем 5 История развития компьютеризации информационных процессов и систем. 5

• Название: Лекция 5 Основные понятия информационных систем 5 История развития компьютеризации информационных процессов и систем. 5
• Анкор: Базы данных
• Дата: 05.01.2022
• Размер: 1.07 Mb.
• Имя файла: Лекции БД.doc
• Тип: Лекция; #324711
• страница: 21 из 24

9.3.2.Файлы с неплотным индексом, или индексно-последовательные файлы

Попробуем усовершенствовать способ хранения файла: будем хранить его в упо­рядоченном виде и применим алгоритм двоичного поиска для доступа к произ­вольной записи. Тогда время доступа к произвольной записи будет существенно меньше. Для нашего примера это будет:

Т=log₂KBO =log₂12500 = 14 обращении к диску.

И это существенно меньше, чем 12500 обращений при произвольном храпении записей файла. Однако и поддержание основного файла в упорядоченном виде также операция сложная.

Неплотный индекс строится именно для упорядоченных файлов. Для этих фай­лов используется принцип внутреннего упорядочения для уменьшения количе­ства хранимых индексов. Структура записи индекса для таких файлов имеет следующий вид:

Значение ключа первой записи блока

Номер блока с этой записью

В индексной области мы теперь ищем нужный блок по заданному значению первичного ключа. Так как все записи упорядочены, то значение первой записи блока позволяет нам быстро определить, в каком блоке находится искомая за­пись. Все остальные действия происходят в основной области. На рис. 9.7 пред­ставлен пример заполнения основной и индексной областей, если первичным ключом являются целые числа.

Индексная область Основная область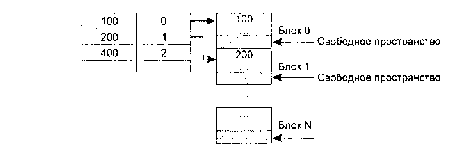



Рис. 9.7. Пример заполнения индексной и основной области при организации неплотного индекса

Время сортировки больших файлов весьма значительно, но поскольку файлы поддерживаются сортированными с момента их создания, накладные расходы в процессе добавления новой информации будут гораздо меньше.

Оценим время доступа к произвольной записи для файлов с неплотным индек­сом. Алгоритм решения задачи аналогичен.

Сначала определим размер индексной записи. Если ранее ссылка рассчитыва­лась исходя из того, что требовалось ссылаться на 100 000 записей, то теперь нам требуется ссылаться всего на 12 500 блоков, поэтому для ссылки достаточ­но двух байт. Тогда длина индексной записи будет равна:

LI = LK + 2=12 + 2= 14 байт.

Тогда количество индексных записей в одном блоке будет равно:

KZIB = LB/LI ⁼ 1024/14 = 73 индексные записи в одном блоке.

Определилм количество индексных блоков, которое необходимо для хранения требуемых индексных записей:

KIB = KBO/KZIB = 12500/73 = 172 блока. |

Тогда время доступа по прежней формуле будет определяться:

Т_поиска=log₂KIB+1 =log₂172+1 = 8 + 1 = 9 обращении к диску.

Мы видим, что при переходе к неплотному индексу время доступа уменьшилось практически в полтора раза. Поэтому можно признать, что организация неплотного индекса дает выигрыш в скорости доступа.

Рассмотрим процедуры добавления и удаления новой записи при подобном ин­дексе.

Здесь механизм включения новой записи принципиально отличен от ранее рас­смотренного. Здесь новая запись должна заноситься сразу в требуемый блок на требуемое место, которое определяется заданным принципом упорядоченно­сти на множестве значений первичного ключа. Поэтому сначала ищется требуе­мый блок основной памяти, в который надо поместить новую запись, а потом этот блок считывается, затем в оперативной памяти корректируется содержимое блока и он снова записывается на диск на старое место. Здесь, так же как и в первом случае, должен быть задан процент первоначального заполнения блоков, но только применительно к основной области. В MS SQL server этот про­цент называется Fill-factor и используется при формировании кластеризованных индексов. Кластеризованными называются как раз индексы, в которых исход­ные записи физически упорядочены по значениям первичного ключа. При внесении новой записи индексная область не корректируется.

Количество обращений к диску при добавлении новой записи равно количестве обращении, необходимых для поиска соответствующего блока плюс одно обра­щение, которое требуется для занесения измененного блока на старое место.

Т_{добавления} = log₂N+1+1 обращений.

Уничтожение записи происходит путем ее физического удаления из основной области, при этом индексная область обычно не корректируется, даже если уда­ляется первая запись блока. Поэтому количество обращений к диску при удалении записи такое же, как и при добавлении новой записи.

9.3.3.Организация индексов в виде B-tree (В-деревьев)

Построение В-деревьев связано с простой идеей построения индекса над уже построенным индексом. Действительно, если мы построим неплотный индекс, то сама индексная область может быть рассмотрена нами как основной файл, над которым надо снова построить неплотный индекс, а потом снова над новым индексом строим следующий и так до того момента, пока не останется, всего один индексный блок.

Мы в общем случае получим нскоторое дерево, каждый родительский блок ко­торого связан с одинаковым количеством подчиненных блоков, число которых равно числу индексных записей, размещаемых в одном блоке. Количество обра­щении к диску при этом для поиска любой записи одинаково и равно количест­ву уровней в построенном дереве. Такие деревья называются сбалансирован­ными (balanced) именно потому, что путь от корня до любого листа в этом дере­ве одинаков.

Построим подобное дерево для нашего примера и рассчитаем для него количе­ство уровней и, соответственно, количество обращений к диску.

На первом уровне число блоков равно числу блоков основной области, это нам известно, — оно равно 12500 блоков. Второй уровень образуется из неплотного индекса, мы его тоже уже строили и вычислили, что количество блоков индексной области в этом случае равно 172 блокам. А теперь над этим вторым уровнем снова построим неплотный индекс.

Мы не будем менять длину индексной записи, а будем считать ее прежней, рав­ной 14байтам. Количество индексных записей в одном блоке нам тоже извест­но, и оно равно 73. Поэтому сразу определим, сколько блоков нам необходимо для хранения ссылок на 172 блока.

KIB₃=КIВ₂/КZIB=172/73 = 3 блока

Мы снова округляем в большую сторону, потому что последний, третий, блок будет заполнен не полностью.

И над третьим уровнем строим новый, и на нем будет всего один блок, в кото­ром будет всего три записи. Поэтому число уровней в построенном дереве равно четырем, и соответственно количество обращений к диску для доступа к произ­вольной записи равно четырем (рис. 9.8). Это не максимально возможное число обращений, а всегда одно и то же, одинаковое для доступа к любой записи.

Т_д = R_{уровней} =4



Рис. 9.8 Построенное В-дерево
Механизм добавления и удаления записи при организации индекса в виде В-дерева аналогичен механизму, применяемому в случае с неплотным индексом.

ИI наконец, последнее, что хотелось бы прояснить, — это наличие вторых назва­ний для плотного и неплотного индексов.

В случае плотного индекса после определения местонахождения искомой запи­си доступ к ней осуществляется прямым способом по номеру записи, поэтому этот способ организации индекса и называется индексно-прямым.

В случае неплотного индекса после нахождения блока, в котором расположена искомая запись, поиск внутри блока требуемой записи происходит последова­тельным просмотром и сравнением всех записей блока. Поэтому способ индек­сации с неплотным индексом называется еще и индексно-последовательньм.