ТАУ_курс лекций. Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7

• Название: Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7
• Дата: 18.01.2023
• Размер: 1.71 Mb.
• Имя файла: ТАУ_курс лекций.doc
• Тип: Лекция; #893368
• страница: 13 из 22

Лекция 9. Частотные критерии устойчивости

Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

 

9.1. Принцип аргумента

 

Запишем характеристический полином САУ в виде

 

D(p) = a₀ (p - p₁) (p - p₂) ... (p - p_n) = 0.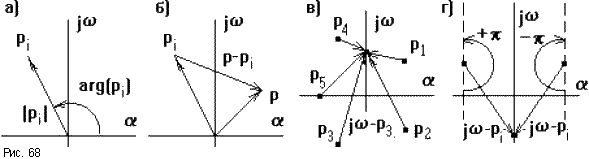

 

 



 

 

Его корни

p_i = _i + j i = |p_i|e^jarg(pi),

 

где arg(p_i) = arctg( i/a_i) + k ,

.

 

Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - p_i изобразится разностью векторов (рис.68б), где p - любое число.

Еcли менять значение p произвольным образом, то конец вектора p - p_i будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как p_i - это конкретное неизменное значение.

В частном случае, если на вход системы подавать гармонические колебания с различной частотой , то p = j , а характеристический полином принимает вид:

D(j ) = a₀ (j - p₁) (j - p₂) ... (j - p_n).

 

При этом концы векторов j - p_i будут находиться на мнимой оси (рис.68в). Если менять от - до + , то каждый вектор j - p_i будет поворачиваться относительно своего начала p_i на угол +p для левых и - p для правых корней (рис.68г).

Характеристический полином можно представить в виде

 

D(j ) = |D(j )|e^{jarg(D(j )}),

где    |D(j )| = a₀ |j - p₁| |j - p₂|...|j - p_n|,

arg(D(j )) = arg(j - p₁) + arg(j - p₂) + .. + arg(j - p_n).

 

Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j ) при изменении от - до + равен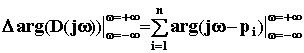

 

= (n - m) - m ,

 

или при изменении от 0 до + получаем

= (n - 2m) ( /2).

 

Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от - до + равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на , а при изменении частоты от 0 до + эта разность умножается на /2.

Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.

 

9.2. Критерий устойчивости Михайлова

 

Так как для устойчивой САУ число правых корней m = 0, то угол поворота вектора D(j ) составит

 

= n /2.

 

То есть САУ будет устойчива, если вектор D(j ) при изменении частоты от 0 до + повернется на угол n /2.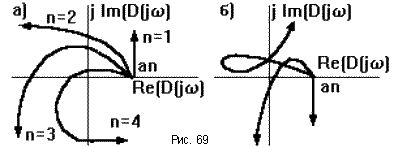



При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так как D(0) = a_n, и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n - ом квадранте  (рис.69а).

Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов  (рис.69б)), то такая САУ неустойчива - это и есть необходимое и достаточное условие критерия Михайлова.

Достоинства. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.

Для облегчения построения годографа Михайлова выражение для D(j ) представляют суммой вещественной и мнимой составляющих:

 

 D(j ) = a₀(j - p₁)(j - p₂)...(j - p_n) = a₀(j )ⁿ + a₁(j )^{n - 1} + ... + a_n = ReD(j ) + jImD(j ),

где

ReD(j ) = a_n - a_{n - 2} ² + a_{n- 4} ⁴ - ...,

ImD(j ) = a_{n - 1} - a_{n - 3} ³ + a_{n- 5} ⁵ - ....

 

Меняя от 0 до по этим формулам находят координаты точек годографа, которые соединяют плавной линией.