Теория потребителя. Лекция тео
 Скачать 0.68 Mb.
|
|
MU1/P1 = MU2/P2 = …MUn/Pn = λ где MU1; MU2; … MUn – предельные полезности потребляемых продуктов; P1; Р2; … Рn – цены на данные продукты; λ – предельная полезность денег. Правило максимизации полезности отражает ситуацию потребительского равновесия. Тогда MU = P·λ, где P·λ – предельные издержки потребителя. Следовательно, если МС = Р·λ, то MU = MC. 4.3. Шкала, кривая и карта безразличия. Предельная норма замещения. Бюджетная линия. Условие равновесия потребителя Основоположники порядковой теории – Слуцкий, Хикс, Парето – исходили из того, что полезность отдельных продуктов измерить нельзя, но можно расставить приоритеты, т.е. построить шкалу предпочтений (или шкалу безразличия). Таблица 4.2
Потребителю безразлично, какой набор выбрать. На основе шкалы безразличия (табл. 4.2) построим кривую безразличия (рис. 4.3). 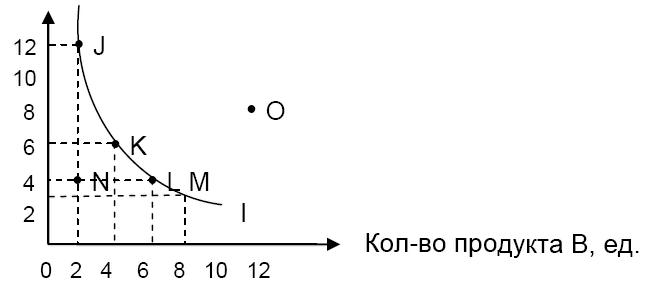 Количество продукта А, ед.Рис. 4.3. Кривая безразличия Каждая точка на графике 4.3 – это одна из комбинаций двух продуктов А и В, выбор которой безразличен потребителю, так как обладает одинаковой совокупной полезностью. На основе графика (см. рис. 4.3) можно сделать следующие выводы: – наборы продуктов, соответствующие точкам J, K, L, M, имеют одинаковую полезность для потребителя (т.е. потребитель безразличен к этим наборам продуктов); – набор продуктов, соответствующий точке N, менее предпочтителен для потребителя; – набор продуктов, соответствующий точке O, более предпочтителен для потребителя. Если через точки N и O провести кривые, параллельные исходной кривой, то получим карту безразличия (рис. 4.4). Карта безразличия представляет собой набор кривых безразличия (вкусы и предпочтения потребителей). Каждая последующая кривая, дальше отстоящая от начала координат, соответствует большей величине совокупной полезности. Комбинация А и В, представленная любой точкой на кривой I4, обладает большей полезностью, чем любая комбинация А и В, соответствующая любой точке на кривых I3, I2, I1. 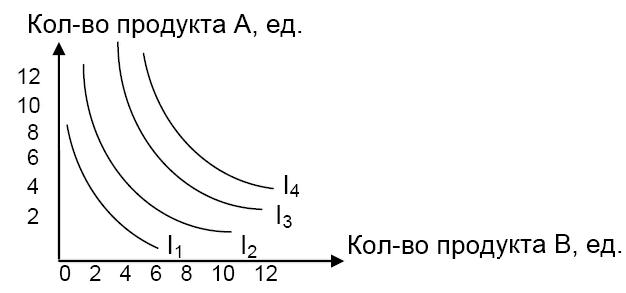 Рис. 4.4. Карта безразличия |