Прокимнов Н. Литература по теме Тема Информационная система как сложная система Вопрос Основные понятия теории систем
 Скачать 1.19 Mb.
|
|
Тема 7. Имитационное моделирование информационных процессов и систем Цели изучения темы: изучить сущность подхода на основе методологии имитационного моделирования к анализу и синтезу информационных процессов и систем. Задачи изучения темы: изучить сущность и границы применимости метода статистических испытаний; изучить основные принципы компьютерной имитации стохастических процессов; понять возможности моделирующих комплексов для создания и применения имитационных моделей. Успешно изучив тему, Вы: Получите представление о: когда применяется и как практически реализуется модель на основе метода статистических испытаний; принципах построения и механизме программной имитации стохастических процессов. Будете знать: как можно создавать модели с помощью систем имитационного моделирования; из чего состоят и как следует анализировать результаты прогонов программной модели. Вопросы темы: 1. Метод статистических испытаний. 2. Концепции имитационного моделирования. 3. Создание имитационных моделей с помощью систем моделирования. 4. Примеры имитационных моделей. Вопрос 13. Метод статистических испытаний. Аналитические модели, рассмотренные ранее, могут с успехом применяться на этапе системного анализа и для решения ряда задач этапа проектирования, когда требования к точности результата не являются слишком строгими. Такими задачами могут быть задачи выбора конфигурации или модели сервера, где требуется определить только класс выбираемого устройства или подсистемы. Однако в ряде практических ситуаций применение аналитических моделей приводит к большой потере точности получаемого результата из-за того, что модели строятся на слишком приблизительном описании реальных процессов. В этих случаях можно использовать подход на основе имитационного моделирования процессов, который позволяет практически с любой степенью точности описать исследуемые процессы и отличается универсальностью применения. Рассмотрение имитационных моделей начнем с метода статистических испытаний. Статистическое моделирование является разновидностью имитационного моделирования и состоит в обработке данных о системе (модели) с целью получения статистических характеристик системы. Чаще всего оно применяется как способ исследования процессов поведения систем в условиях, когда внутренние взаимодействия в системах неизвестны, и построение аналитической модели явления затруднено или вовсе неосуществимо. Метод может применяться и на этапе системного анализа информационных систем, но основными для его применения являются задачи исследования операций, массового обслуживания и многие другие, связанные со случайными процессами. Эти задачи возникают в основном на этапах системного проектирования и разработки. Смысл метода Монте-Карло состоит в том, что исследуемый процесс моделируется путем многократных повторений его случайных реализаций (Рис. 30). 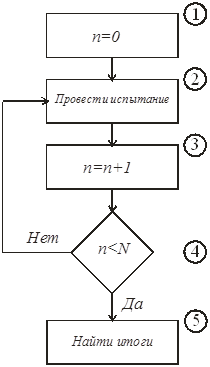 Рис. 30. Схема метода Монте-Карло Единичные реализации называются статистическими испытаниями, в силу чего метод называется также методом статистических испытаний. Поясним применение метода Монте-Карло к решению задачи оценивания величины критического пути сетевой модели, показанной на Рис. 28. На примере этой модели рассматривался метод нахождения величины критического пути при детерминированных условиях. Будем теперь предполагать, что длительности работ не являются неизменными, а варьируются в зависимости от случайных факторов, что, как уже отмечалось, встречается на практике значительно чаще. Каждое испытание (блок 2 на Рис. 30) будет включать два шага: 1) генерацию значений длительностей всех работ t(i,j) на графе сетевой модели; 2) расчет на основе применения описанного ранее метода критического пути величины критического пути Ткр для данной совокупности значений длительностей работ. Шаг 1 выполняется на основе наблюдений за случайными величинами, представляющими собой длительности работ графа. Результат этих наблюдений выражается некоторым законом распределения вероятностей. Генерация случайных величин для каждой их реализации проводится с помощью программных средств. Эти средства строятся на основе специальных алгоритмов получения псевдослучайных чисел, т.е., не являющихся, строго говоря, результатом измерения характеристик каких-то физических явлений, а достаточно точно их имитирующих. К настоящему времени предложено и реализовано большое количество этих алгоритмов, которые позволяют, с одно стороны, получить достаточно хорошие выборки значений и, с другой стороны, весьма сводят к минимуму потребности в вычислительных ресурсах, которые необходимы для выполнения программ. Шаг 2 в данном случае состоит в обработке данных, полученных в результате выполнения шага 1, а именно, массива N значений . Если задача ставится, как задача нахождения только среднего значения , то обработка сведется к выполнению лишь одной операции: 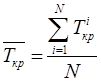 ,где - значение , полученное в i-ом испытании. Однако данные, собранные в результате моделирования, содержат в себе более полную информацию относительно исследуемого показателя. Поэтому целесообразно использовать результат для построения гистограммы частот значений . Например, моделирование методом Монте-Карло графа Рис. 28, в котором длительности работ распределены по равномерному закону со средними значениями, показанными на рисунке, и величиной полуинтервалов изменений равными 1/3 средних значений, даст следующие результаты: Гистограмма распределения длины критического пути
Tкр.ср=16.1486. Представление гистограммы частот в графическом виде дано на Рис. 31. 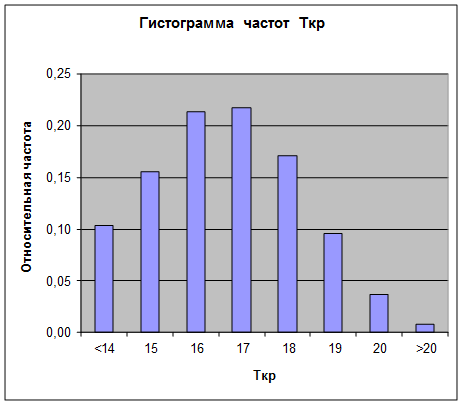 Рис. 31. Пример гистограммы частот По этой гистограмме можно оценить величину вероятности выполнения совокупности работ в течение заданного времени  . Например, если нужно оценить, с какой вероятностью может быть выдержан срок =18, то находим: .что можно считать очень большой величиной. Ниже приводится текст программы на языке С++ для выполнения на ее основе практического задания.
Значения параметров моделирования задаются в разделе с заголовком (строкой комментария) «Параметры моделирования» (выделен в вышеприведенном тексте полужирным шрифтом). В разделе задаются:
Результаты выводятся в файл, обозначаемый переменной reportfile. Недостатком метода Монте-Карло являются большие затраты машинного времени, требуемые для достижения большей статистической точности (известно, что для уменьшения дисперсии результата в раз, число испытаний необходимо увеличить в раз). Вопрос 14. Концепции имитационного моделирования. Аналитические модели, как и модели вообще строятся для некоторых допущений. В случае аналитических моделей эти допущения могут ухудшать точность получаемых на их основе результатов в силу ограничений, накладываемых используемым математическим аппаратом. Кроме того, получение аналитических выражений для расчета показателей часто представляет большую трудность. Альтернативным подходом к решению задач оценки показателей является исследование системы на основе имитационной модели, с помощью которой можно получить результаты для случаев произвольных распределений временных интервалов и других случайных величин. Такую модель можно построить с помощью специальной моделирующей системы, что ускоряет процесс создания, улучшает характеристики конечного результата (программной модели) и имеет ряд других достоинств. Как уже обсуждалось ранее поведение (процесс функционирования) динамической дискретной системы можно рассматривать как последовательность состояний  в моменты времени  . При этом факты смены состояния системой рассматриваются как события. В основу идеи имитационного моделирования положен принцип, согласно которому на ЭВМ осуществляется воспроизведение (имитация) процесса функционирования исследуемой системы в контексте смены ее состояний в результате происходящих в ней событий. В процессе проведения имитации собираются данные о состоянии системы или отдельных ее элементов в определенные моменты времени, что позволяет в конце процесса моделирования провести агрегирование и обработку собранных данных и получить значения нужных исследователю показателей.Пусть, например, нам необходимо исследовать работу системы массового обслуживания (СМО) с очередью и одним обслуживающим прибором (Рис. 32).  Рис. 32. Одноканальная система массового обслуживания с очередью Заявки, образующие входящий поток, поступают в систему в случайные моменты времени. Если обслуживающий прибор (канал) свободен, заявка принимается на обслуживание, которое продолжается некоторое время (его величина является, как правило, также случайной), после чего она уходит из системы (выходящий поток). Если в момент прихода заявки канал занят, заявка попадает в очередь ждущих заявок. Решая задачу нахождения показателей системы, для описания состояния процесса достаточно использовать один параметр , который означает число заявок в системе в момент времени . Имитацию процесса обслуживания заявки в можно провести, определяя моменты ожидаемого изменения состояния (наступления события), связанных с изменением состояния . В данном случае, это моменты поступления очередной заявки в систему и моменты окончания обслуживания заявки, находящейся в обслуживающем приборе. Моменты наступления будущих событий могут быть найдены на основе рекуррентных выражений с помощью функций распределения интервалов времени путём проведения случайных испытаний аналогично тому, как это производилось в методе статистических испытаний. Это позволяет построить алгоритм имитации, состоящий из повторения следующей совокупности шагов: находится момент наступления ближайшего события, событие с минимальным временем — наиболее раннее событие; стрелки модельных часов передвигаются на этот момент времени; определяется тип происшедшего события; в зависимости от типа события модифицируются значения переменных, описывающих состояние системы (в данном случае, число находящихся в системе заявок), и определяются следующие моменты наступления событий. Логическая последовательность шагов моделирования показана на Рис. 33. 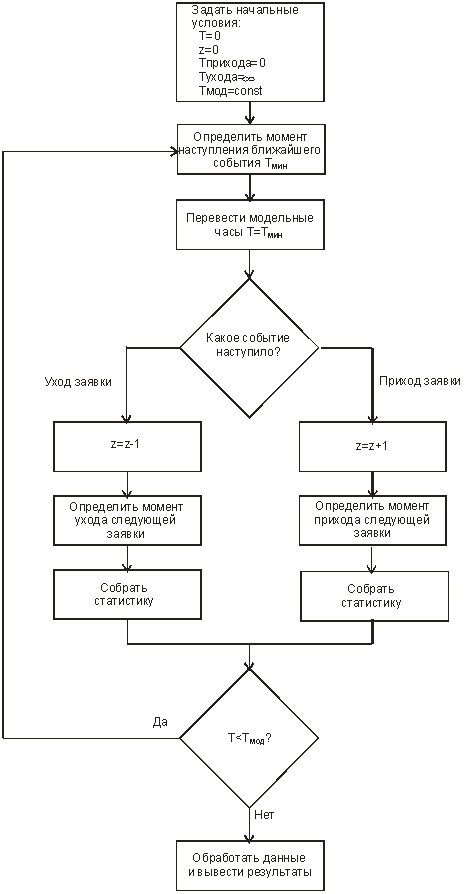 Рис. 33. Блок-схема имитации процессов в одноканальной СМО с очередью В процессе выполнения алгоритма производится накопление значений существенных параметров моделируемой системы. По окончании моделирования осуществляется статистическая обработка полученных величин и выдача результатов. Описанный алгоритм носит название событийного алгоритма. Альтернативным способом построения алгоритма имитационного моделирования является перемещение по временной оси с фиксированным интервалом (шагом). После каждого перехода на новую временную отметку проводится сканирование всех протекающих в моделируемой системе процессов и выявление всех свершившихся на данный момент существенных событий. Такой алгоритм носит название пошагового алгоритма. Преимуществом пошагового алгоритма является простота его программной реализации. Вместе с тем, в условиях, когда наступление событий, обусловленных разными процессами, происходит с сильно отличающимися интервалами, то значительное время моделирования оказывается затраченным впустую (например, при моделировании производственного процесса на предприятии, работающем в односменном режиме, все вечернее и ночное время программная модель не будет выполнять никакой содержательной работы). Поэтому большинство программных реализаций имитационных моделей использует событийный алгоритм имитации. Имитационное моделирование представляет собой процесс, реализуемый с помощью средств вычислительной техники, что позволяет автоматизировать решение таких задач как: 1. Создание или модификация имитационной модели. 2. Проведение модельных экспериментов и интерпретация получаемых результатов. В случаях разработки сложных моделей, предназначенных для проведения большого объема экспериментов, для решения этих задач используются моделирующие комплексы (системы). Имитационное моделирование как информационная технология включает несколько основных этапов. На этапе структурного анализа процессов проводится формализация реального процесса, его декомпозиция на подпроцессы, которые могут также подвергаться декомпозиции. Задачи, решаемые на этом этапе, соответствуют задачам создания модели деловых процессов, вместе с тем, в зависимости от применяемых средств моделирования результат может потребовать преобразования формы представления в вид, наиболее полно соответствующий задачам, решаемым на дальнейших шагах. Описание модели в вербальном, графическом или полуформализованном виде должно быть представлено на специальном (формальном) языке для ввода в моделирующую систему. При этом могут применяться: Ручной способ. Описание составляется на языке какой-либо системы моделирования, например,GPSS, Pilgrim или алгоритмическом языке, например, Visual Basic (размер результирующего текста в последнем случае будет многократно превосходить размер текста на языке специальных систем). Автоматизированный способ. Текст на формальном языке получается в результате автоматической генерации описания, которое строится в интерактивном режиме с помощью высокоуровневого графического конструктора. Такой конструктор, которым оснащена, в частности, система Pilgrim, позволяет фактически совместить этап разработки программной модели с этапом системного анализа. Созданное формальное описание далее преобразуется в компьютерную программу, способную воспроизводить реальные процессы. Преобразование, которое обычно представляет собой трансляцию и редактирование связей, осуществляется в некоторой программной среде, может проводиться в двух режимах. Интерпретация. В этом режиме специальная программа-интерпретатор осуществляет всю процедуру имитации, непосредственно выполняя инструкции формального описания. Примером системы, где предусмотрен режим интерпретации, является система GPSS. Компиляция. В этом режиме на основе формального описания создается отдельная программа (исполнительный модуль), который может запускаться независимо от программной среды, в которой он был создан. Примером системы, где предусмотрен режим интерпретации, является система Pilgrim. Целью следующего этапа является обоснование модели, заключающегося в демонстрации пригодности модели для получения нужных показателей, т.е., обеспечение необходимых точности и надежности получаемых на ее основе результатов. Основной, последний этап моделирования сводится к проведению машинных экспериментов с программной моделью, сбору, накоплению, обработке и анализу собранных данных. Вопрос 15. Создание имитационных моделей с помощью систем моделирования. С началом развития средств вычислительной техники и связанного с ним прогресса в области теории и практики имитационного моделирования создано более 300 языков моделирования дискретных систем и процессов. Одной из наиболее старых систем моделирования является система GPSS, которая была разработана сотрудником компании IBM Джеффри Гордоном в 1961 году (он же был и создателем описанного выше событийного алгоритма). Система на сегодняшний день остается в числе широко распространенных, к тому же в своей несколько усеченной версии доступна для свободного применения. Поэтому основные концепции моделирующих комплексов рассмотрим на примере системы GPSS. Система GPSS (General Purpose Simulating System)предназначена для построения имитационных моделей систем с дискретным множеством состояний различной степени сложности и включает в себя язык моделирования и программу-интерпретатор текста описания модели. Элементами языка моделирования системы GPSSявляются абстрактные объекты и операции. Объекты в системе подразделяются на 7 категорий и 15 типов. К первой категории и первому типу относятся динамические объекты, называемые транзактами, представляющие собой единицы исследуемых потоков. Работа GPSS-модели сводится к перемещению транзактов между блоками модели согласно определенным в описании модели правилам. Содержательный смысл транзактов вытекает из смысла моделируемой системы или процесса. В процессе моделирования транзакты могут создаваться и уничтожаться, в каждый момент в модели может находиться много транзактов, но перемещается только один. Основу GPSS-интерпретатора составляет диспетчерская программа (симулятор), выполняющая следующие функции: перемещает транзакты по заданным маршрутам; планирует происходящие в модели события посредством выявления моментов наступления событий в будущем и их реализации в порядке возрастания значений моментов наступления; производит сбор статистики о функционировании модели; осуществляет продвижение модельного времени в процессе моделирования. Время в модели дискретно, масштаб (соотношение между безразмерной единицей модельного времени и единицей реального времени) определяется разработчиком. Для наглядного представления модели может применяться язык блок-схем. Блок-схемы представляют собой набор фигур, соединенных линиями, показывающими порядок прохождения транзактов по блокам модели. Блок может иметь несколько входящих в него линий, что указывает на то, что он является общим для нескольких последовательностей событий, а также несколько исходящих линий, что указывает на то, что выходящий транзакт может направляться в разные блоки в зависимости от некоторых правил или условий. В процессе выполнения программной модели транзакты хранятся в списках. Этих списков всего пять, но в каждый момент времени транзакт может находиться только в одном. Список текущих событий хранит транзакты, планируемое время наступления событий для которых равно или меньше текущего времени (транзакты должны были уже перемещаться ранее, но были заблокированы). Список будущих событий хранит транзакты, планируемое время наступления событий для которых больше текущего времени (транзакты должны переместиться в будущем). Список отложенных прерываний хранит отдельные транзакты, обслуживание которых занятыми или захваченными устройствами было прервано. Список пользователя хранит транзакты, которые пользователь удалил из списка текущих событий и поместил в список временно пассивных. Список синхронизируемых сообщений хранит транзакты, находящиеся в данный момент в состоянии сравнения. В зависимости от различных условий транзакты помещаются в соответствующие списки. Симулятор продвигает каждый транзакт до того момента, пока его продвижение не будет заблокировано занятым блоком или когда транзакт войдет в блок, задающий временную задержку. Задержанные транзакты попадают в список будущих событий, заблокированные транзакты – в список текущих событий. Просматривая список текущих событий, симулятор пытается передвинуть содержащиеся в нем транзакты к следующим блокам модели. Если это сделать нельзя, то системные часы, хранящие абсолютное время модели, переводятся на момент наиболее раннего из будущих событий, соответствующий транзакт переносится в список текущих событий и передвигается, если возможно, к следующему блоку модели. Если рассматриваемый транзакт входит в блок задержки, то он снова попадает в список будущих событий. В случае блокировки транзакт остается в списке текущих событий. Каждому из GPSS-объектов выделяется участок оперативной памяти, в котором в процессе моделирования хранятся атрибуты объекта. Те из них, которые доступны пользователю, носят название стандартных числовых атрибутов (СЧА). Так, время нахождения транзакта в модели (резидентное время) хранится в СЧА с именем M1. Для различных объектов модели (прибор, многоканальное устройство, очередь) определены свои СЧА, что отражается в их именах, первая часть которых идентифицирует тип объекта, а вторая часть его номер или имя. Генерация случайных чисел осуществляется с помощью восьми встроенных генераторов, что позволяет назначить каждому из имитируемых в модели случайных процессов свой собственный генератор. Модель в системе GPSS описывается с помощью последовательности операторов, каждый из которых может относиться к одному из трех типов. Блоки, образующие описание основных действий и их последовательности (блоки образую основу блок-схемы модели). Декларативные операторы, необходимые для описания переменных, функций и памяти (многоканальных устройств). Команды, применяемые как для описания логических правил выполняемых действий, так и для организации взаимодействия пользователя с моделью. Описание блока состоит из нескольких полей, отделяемых друг от друга пробелами или ограничителями (необязательные части заключены в квадратные скобки): [<Метка>]<Операция><Операнды>[<Комментарии>]. Метка начинается с латинской буквы. Операция означает команду, выполняемую при входе транзакта в блок. Операнды необходимы для задания значений характеризующих операцию параметров. Комментарии служат целям документирования и отделяются от операндов символом «;» или символом «*». Объект, переменная и местоположение в программе обозначается именем, образуемым как последовательность символов длиной не более 250, начинающихся с символа и не совпадающего с ключевым словом языка. Вопрос 16. Примеры имитационных моделей. Рассмотрим несколько примеров моделирования с помощью системы GPSS. Для реализации модели использована свободно распространяемая версия системы GPSS World Student Version 5.2.2. Начнем с ранее рассмотренной модели одноканальной СМО (Рис. 32). Блок-схема, реализующая имитацию протекающих в этой СМО процессов, показана на Рис. 34. 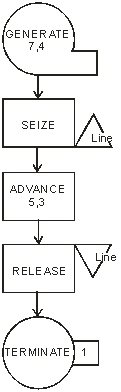 Рис. 34. Блок-схема GPSS-модели одноканальной СМО с очередью Соответствующее описание с помощью операторов языка GPSS имеет вид:
В приведенном описании присутствуют пять блоков. Первый блок, GENERATE, обеспечивает поступление в модель транзактов (заявок в СМО). Транзакты поступают через интервалы времени, определяемые как равномерно распределенные случайные величины со средним значением 7 и полуинтервалом (размахом) 4, что задается операндами блока. Второй блок, SEIZE, осуществляет имитацию попытки захвата транзактом устройства с именем Line. Если попытка оказывается успешной (устройство Line свободно), транзакт попадает в это устройство и остается в нем на протяжении времени, которое определяется как равномерно распределенная случайная величина со средним значением 5 и полуинтервалом 3. Эти значения задаются в третьем блоке, ADVANCE, имитирующем процесс обслуживания. Если попытка захвата устройства оказывается неуспешной, то транзакт остается ждать освобождения устройства (возможно, вместе с другими ожидающим транзактами). Четвертый блок, RELEASE, имитирует факт (событие) завершение обслуживания, состоящего в освобождении транзактом устройства с именем Line. Пятый блок, TERMINATE, имитирует уход транзакта из системы. После выполнения команды Create Simulation и запуска модели командой Start с операндом 1000 (число транзактов, которые должны пройти через модель в процессе моделирования) получаем отчет, показанный на Рис. 35.  Рис. 35. Отчет с результатами моделирования одноканальной СМО В верхней части отчета приводятся значения времени начала (0.000) и окончания (7049.623) моделирования, число блоков модели (5), число устройств модели (1) и число многоканальных устройств (0). Вслед за этим приводятся сведения по каждому имени, каждому блоку, каждому устройству модели вместе с относящейся к ним статистикой, после чего дается информация о списках текущих (CEC) и будущих (FEC) событий. Построенная модель позволяет достаточно точно (в предположении того, что имеется достаточно точная информация относительно распределений интервалов между приходами заявок и продолжительностью их обслуживания) имитировать реальные процессы, но содержит довольно скудную информацию относительно показателей качества моделируемой системы. В частности, значительный интерес для системного аналитика могут представлять сведения, касающиеся образующейся очереди заявок. Например, если исследуется процесс обработки потока файлов-заявок в информационной системе, характеристики очереди будут во многом определять требования к производительности сервера и объемам памяти, необходимой для организации хранения ждущих заявок. Для сбора и вывода таких данных в системе GPSS предусмотрены специальные средства. Проиллюстрируем их применение на примере той же одноканальной СМО, модифицированная блок-схема модели которой показана на Рис. 36. 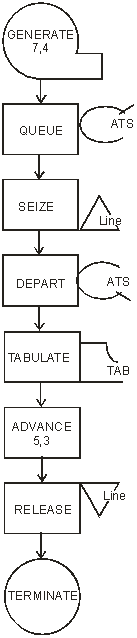 Рис. 36. Модифицированная блок-схема GPSS-модели одноканальной СМО с очередью Соответствующее описание на языке GPSS имеет вид:
В новом варианте модели для сбора статистики появились блоки, с именами QUEUE и DEPART. Блок QUEUE используется для размещения в нем транзактов, которые не могут быть продвинуты к следующему блоку в силу его занятости. Формат QUEUE оператора включает в качестве обязательного операнд с именем очереди (в данном случае ATS). Когда появляются условия для дальнейшего продвижения транзакта, он должен покинуть очередь, что обеспечивается блоком DEPART (обязательный операнд оператор указывает на имя этой очереди). Система GPSS обеспечивает в случае использования этих блоков автоматические регистрацию и накопление статистики относительно времени нахождения транзактов в очереди и ее размере. Средние значения этих величин выводятся в стандартном отчете. Однако система предоставляет средства для сбора более подробной информации в виде гистограмм, аналогичных рассмотренным в разделе, посвященном моделированию по методу Монте-Карло. Для этого необходимо в GPSS-модели описать структуру гистограммы, что реализуется с помощью декларативного оператора (карты) TABLE, и внести в нужных точках модели оператор TABULATE, который обеспечивает автоматическое обновление данных таблицы. Для данной модели в операторе TABLE указаны:
Отчет с результатами моделирования показан на Рис. 37. 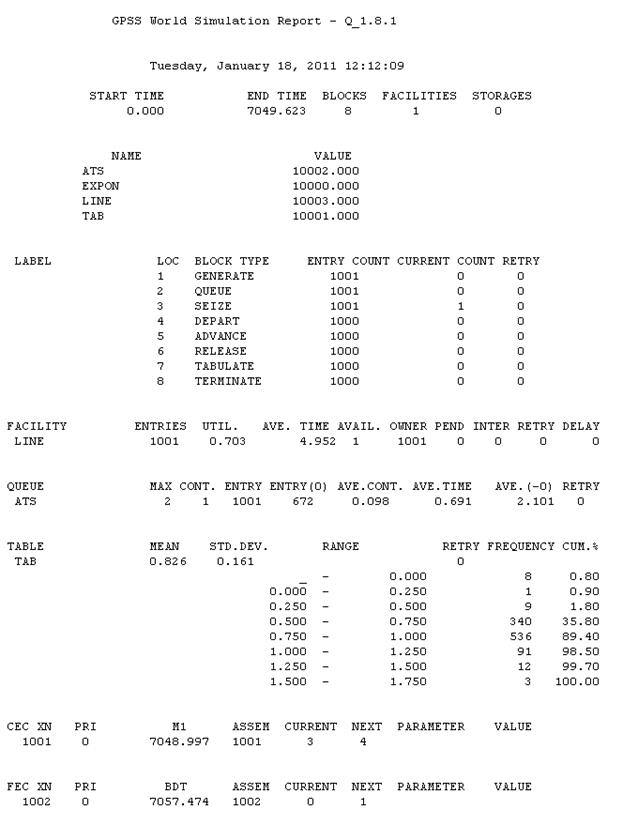 Рис. 37. Расширенные результаты моделирования одноканальной СМО с очередью Теперь помимо средних значений размера очереди (AVE.CONT) и времени нахождения в ней транзактов (AVE.TIME) в строке QUEUE выводится и статистика по частотам (FREQUENCY) и интегральной доле в процентах (CUM%) попаданий длительности нахождения в очереди в соответствующие интервалы (RANGE). Эти данные можно представить более наглядно в виде диаграммы, которую легко построить с помощью имеющихся графических программ (пример такой диаграммы приводился в разделе с описанием метода Монте-Карло). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||