РГР по статистике (варианты 1-30) (1). Методические указания по выполнению контрольной работы по статистике

• Название: Методические указания по выполнению контрольной работы по статистике
• Дата: 06.06.2021
• Размер: 319.79 Kb.
• Имя файла: РГР по статистике (варианты 1-30) (1).docx
• Тип: Методические указания; #214511
• страница: 28 из 30

Расчетно-графическая работа
по курсу «Статистика» (вариант 28)

1. Методические указания по выполнению
контрольной работы по статистике

Задание к контрольной работе включает 150 вариантов. Каждый вариант включает 10 задач.

В заголовке контрольной работы должны быть четко написаны: название дисциплины, фамилия, имя и отчество студента, название факультета и группы, номер зачетной книжки студента, номер варианта.

Вариант контрольной работы выбирается:

1) для очного отделения – по указанию преподавателя;

2) для заочного отделения вариант контрольной работы выбирается по последним трем цифрам номера зачетной книжки. Например, если последние цифры 240, то выбирается вариант 90 (240-150). Если последние цифры 340, то выбирается вариант 40 (340-150-150) и т.д.

Студент допускается к сдаче экзамена только после получения зачета по контрольной работе.

ВНИМАНИЕ!!! Расчеты проводить с точностью до ПЯТИ значащих цифр (например, 1.2345, 1234.5, 123456, 123.45, 12.345% и т.п.).

2. Задание к контрольной работе

Задача 1. Данные о полной себестоимости товарной продукции и стоимости товарной продукции в оптовых ценах за 2006г. по 25 предприятиям приведены в таблице 1. Для выявления зависимости между данными показателями произведите группировку, образовав 4 групп с равными интервалами (группировочный признак – стоимость товарной продукции).

В каждой группе подсчитайте:

109. 
     Частоты и частости.
     
110. 
     Стоимость товарной продукции – в процентах к итогу, а также в среднем на одно предприятие.
     
111. 
     Себестоимость товарной продукции – в процентах к итогу, а также в среднем на одно предприятие.
     
112. 
     Затраты, приходящиеся на 1 рубль товарной продукции.
     

Результаты группировки оформите в таблице.

Ряд распределения по стоимости товарной продукции изобразите на графике в виде гистограммы частостей.

Таблица 1

Номер предприятия	1	2	3	4	5	6	7	8	9	10
Стоимость товарной продукции, млн руб.	442	530	181	133	235	191	457	353	139	439
Себестоимость товарной продукции, млн руб.	238	262	132	116	225	215	375	324	95	234

Продолжение таблицы 1

11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
397	491	160	238	183	320	507	434	480	320	130	338	519	335	518
243	279	153	160	188	322	366	301	332	286	99	261	316	216	396

Задача 2. На основании данных о средней стоимости товарной продукции, полученным в результате группировки при решении задачи №1, рассчитайте:

109. 
     Среднюю стоимость товарной продукции.
     
110. 
     Моду и медиану (аналитически и графически).
     
111. 
     Дисперсию и среднеквадратическое отклонение.
     
112. 
     Коэффициент вариации.
     

Сравните средние (среднюю стоимость товарной продукции, моду, медиану, дисперсию и среднеквадратическое отклонение), рассчитанные по группированным данным и рассчитанные по массиву исходных данных по всем 25 предприятиям.

Замечание. При расчете дисперсии используйте формулу для несмещенной оценки дисперсии.

Замечание. Для расчета средних по массиву исходных данных воспользуйтесь электронными таблицами Microsoft Excel. Используйте статистические функции СРЗНАЧ(), МОДА(), МЕДИАНА(), ДИСП() и СТАНДОТКЛОН().

Замечание. При решении задач 3 и 4 используйте значение дисперсии, рассчитанное по массиву исходных данных.
Задача 3. По результатам задачи №2 найдите доверительный интервал для средней стоимости товарной продукции при доверительной вероятности =0,99.

При расчете средней ошибки выборки используйте данные о том, что объем генеральной совокупности равен 350 (это число предприятий, выпускающих аналогичную продукцию и которые могут быть обследованы).

Значения t-критерия Стьюдента при уровне доверительной вероятности 0,90, 0,95 и 0,99 приведены в приложении 1.
Задача 4. По данным задачи №1 рассчитайте необходимую численность бесповторной выборки, чтобы при доверительной вероятности 0,95 предельная ошибка выборки _x для средней стоимости товарной продукции не превысила 10 млн. руб. Объем генеральной совокупности указан в задаче 3.
Задача 5. По данным таблицы 2 рассчитайте среднегодовую величину активов банка за каждый год, а также среднюю величину активов за каждый квартал.

Таблица 2

1.01.06	1.04.06	1.07.06	1.10.06	1.01.07	1.04.07	1.07.07	1.10.07	1.01.08
560	571	548	531	573	601	637	668	721

Задача 6. По данным таблицы 2 рассчитайте показатели изменения ряда динамики по цепной и базисной системам:

1) Абсолютный прирост.

2) Темпы прироста.

3) Средний абсолютный прирост в каждом году (отдельно абсолютный прирост в среднем за квартал и в среднем за месяц).

4) Средние темпы прироста в каждом году (отдельно темпы прироста в среднем за квартал и в среднем за месяц).

Замечание. При расчете данных за 2007 год в качестве базового момента времени используйте 1.01.2007.

Замечание. Рассчитанные темпы прироста выражайте в процентах (например, 12.345%, 1.2345% и т.п.).

Задача 7. В таблице 3 приведены данные о продаже однородной продукции в магазинах города за два периода. Рассчитайте среднюю розничную цену товара в целом по городу за каждый период. Укажите, какие виды средних используются в каждом случае.

Таблица 3

Номер магазина	I квартал 2006 года			II квартал 2006 года
	Цена, тыс руб.	Объем продаж, шт.	Цена, тыс руб.		Объем продаж, тыс.руб.
1	412	88	407		33781
2	362	37	453		11325
3	366	33	358		12530

Задача 8. По данным задачи 7 рассчитайте:

109. 
     Индивидуальные индексы цен и физического объема продаж.
     
110. 
     Общий индекс цен.
     
111. 
     Общий индекс товарооборота в сопоставимых ценах.
     
112. 
     Общий индекс товарооборота в действующих ценах.
     

Разложите на факторы изменение товарооборота за счет изменения цен и физического объема продаж.
Задача 9. По данным задачи 7 рассчитайте:

82. 
    Индекс цен переменного состава (индекс средней цены).
    
83. 
    Индекс цен постоянного состава.
    
84. 
    Индекс структурных сдвигов.
    

Покажите взаимосвязь исчисленных индексов.
Задача 10. С целью изучения тесноты связи между стоимостью товарной продукции в оптовых ценах и себестоимостью товарной продукции:

1) Измерьте тесноту связи между этими показателями с помощью: а) линейного коэффициента корреляции и б) коэффициента ранговой корреляции Спирмена.

2) Рассчитайте доверительный интервал для коэффициента корреляции при доверительной вероятности 0,99.

3) Проверьте гипотезу о значимости коэффициента корреляции.

4) Оцените уравнение линейной парной регрессии Y=a₀+a₁×X;

5) Постройте диаграмму рассеяния и линию уравнения линейной регрессии;

6) Спрогнозируйте себестоимость товарной продукции, объем прибыли и рентабельность продаж, если планируемый объем товарной продукции в следующем году 600.

7) Рассчитайте доверительные интервалы для полученных прогнозов себестоимости товарной продукции, объема прибыли и рентабельности продаж при доверительной вероятности 0,99.

8) Представьте зависимость между себестоимостью и стоимостью товарной продукции с помощью: а) уравнения параболы Y=a₀+a₁×X+a₂×X², б) степенной функции Y=a₀×X^а1, в) логарифмической функции Y=a₀+a₁×ln(X), г) экспоненциальной функции Y=a₀×e^а1×X и д) уравнения гиперболы .

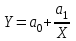9) Рассчитайте значения коэффициента детерминации R² для каждого варианта аппроксимации.

10) Обоснуйте c помощью коэффициента детерминации R² какое из уравнений более точно описывает зависимость между изучаемыми показателями.

Замечание. Для решения этой задачи рекомендуется использовать какое-либо программное обеспечение статистического анализа данных. В частности, электронные таблицы Microsoft Excel обладают всем необходимым инструментарием для решения данной задачи.