9-10 кл Мхан колебания модуль на 8 уроков. Модуль Механические колебания
 Скачать 310 Kb. Скачать 310 Kb.
|
|
Решение задач [26,27]: За 5 с тело совершило 8 полных колебаний. Вычислите период и частоту колебаний тела.
На пружине с жесткостью 3 Н/м тело массой 2 кг совершает механические колебания. Растяжение пружины составило 2 см. Вычислите скорость движения тела, если полная механическая энергия системы равна 3 Дж. Силой трения пренебречь.
Тело совершает колебательное движение на пружине с жесткостью 5 Н/м. Амплитуда колебаний составила 10 см. Вычислите массу тела, если максимальная скорость движения тела составила 0,2 м/с. Силой трения пренебречь.
Итоги урока. Домашнее задание: §2.1-2.3. упр.2.1№3, упр. 2.2 №3, упр. 2.3 №2. Дата проведения 20.11.07 Урок № 21 Тема: Содержательно- поисковый УЭ №1.2. Колебания математического и пружинного маятника. Свободные и вынужденные колебания. Резонанс. Цели и задачи:Развитие представлений о маятниках, развитие у учащихся представлений об основных свойствах превращения энергий при колебательном движении, о свободных и вынужденных колебаниях и резонансе. Задачи развития:Уметь выполнять расчеты по известным формулам, определять симметрию в единицах измерения. Задачи воспитания: Развитие логического мышления, умения выполнения анализа. Ход урока: Организационный момент. Подготовка к уроку. Объявление темы и цели урока. 3 минуты. Физический диктант: Закончите предложения: Механические колебания представляют собой…(периодически повторяемое движение) Отклонение тела от положения равновесия называют…(смещением) Продолжительность одного полного колебания называют…(периодом) Частота колебаний это…(число колебаний в единицу времени) Совпадение собственной частоты колебания системы с частотой внешней силы называют..(резонансом) При колебательном движении потенциальная энергия переходит в …(кинетическую) [28]. Запишите формулы вычисления: Периода. Потенциальной энергии упруго деформированной пружины. Частоты. Полной механической энергии колебательной системы. Представление презентаций «Пружинный маятник» и «Математический маятник». Демонстрация опытов с пружинным и математическим маятниками. Теоретическая часть [24,16,25]: Комбинацию тело – пружина называют пружинным маятником. 2. Когда пружина не деформирована, т. Е. не сжата и не растянута, сила упругости на тело не действует. 3. При деформации пружины на тело начинает действовать сила упругости, направленная к точке положения равновесия. Она и заставляет тело совершать колебательное движение. 4. Скорость колеблющегося тела при максимальном отклонении от положения равновесия равна нулю. 5. Скорость колеблющегося тела при прохождении положения равновесия максимальна. 6. Скорость при колебаниях периодически изменяется. 7. Период колебания пружинного маятника определяется по следующей формуле: 8. Если у маятника тело (груз) имеет размеры много меньшие, чем длина нити, и масса нити тоже ничтожно мала по сравнению с массой тела, то такой маятник называют математическим. 9. При малых углах отклонения математического маятика от положения равновесия можно считать, что его движение похоже на движение пружинного маятника (до 80). 10. Период колебания математического маятника можно вычислить по формуле 11. Циклическая частота колебаний связана с периодом колебаний следующим образом: 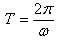 . .12. Связь циклической частоты системы, скорости и ускорения: 13. Колебания, которые после возбуждения происходят без внешних воздействий, называются свободными. 14. Вынужденными колебаниями называют колебательное движение под действием периодической внешней силы. Решение задач [29]: Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Как относятся длины математических маятников, если за одно и то же время один из них совершает 10, а другой 30 колебаний?
За одно и тоже время один математический маятник делает 50 колебаний, а второй 30. Найти их длины, если один короче другого на 32 см.
Тело массой 1 кг колеблется на пружине с жесткостью 4 Н/кг. Вычислите циклическую частоту, скорость и ускорение колебаний, если растяжение пружины составило 1 м.
|

 =5с
=5с  ано:
ано: =0,15м
=0,15м  =250H/ м
=250H/ м 1/l2-?
1/l2-?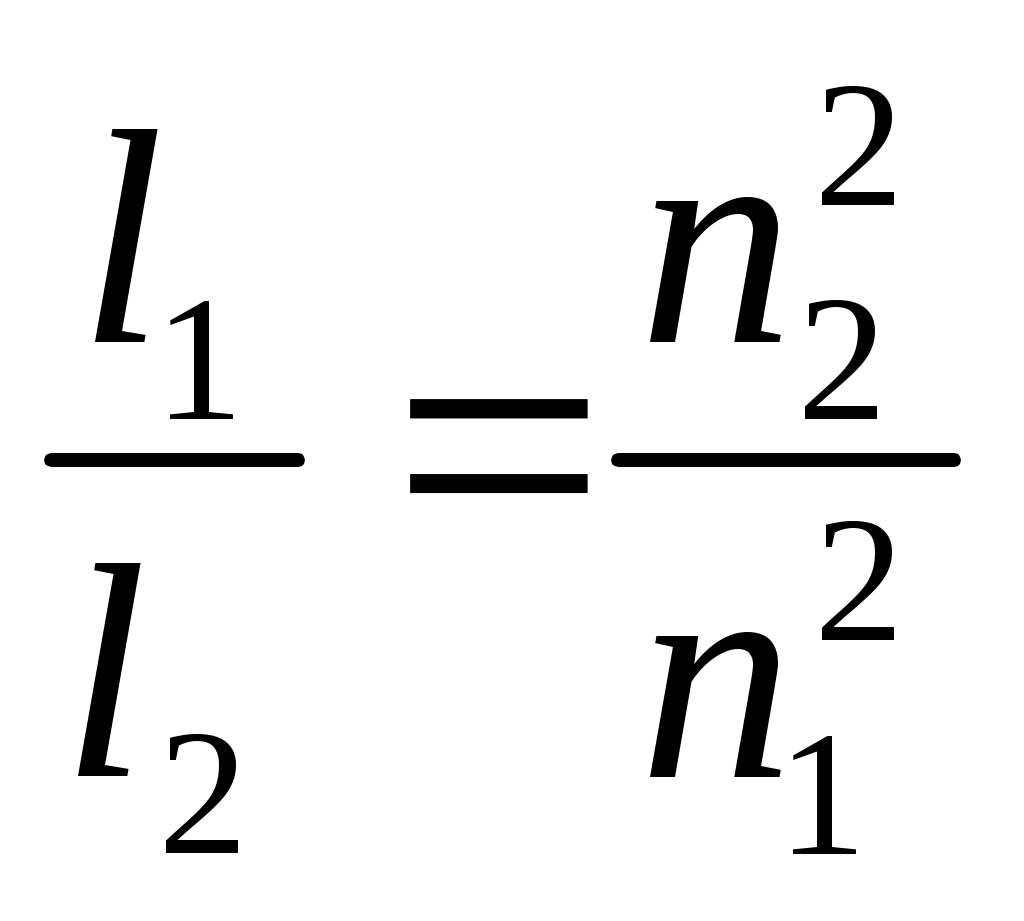
 ано:
ано: