Курсовая работа по СДН. Мониторинг эффективности применения бгс скважин в условиях залежи 8 Ромашкинского месторождения нгду альметьевнефть
 Скачать 347.31 Kb. Скачать 347.31 Kb.
|
3 РАСЧЕТНЫЙ РАЗДЕЛ3.1 Ассоциативный и многофакторный анализ влияния факторов на эффективность применения БГС на промысловом объектеАссоциативный анализ показывает влияние того или иного фактора, как например: длина горизонтального участка; глубина залегания пласта; проницаемость; пористость; толщина пласта – на эффективность применения проводки бокового горизонтального ствола в виде прироста добычи нефти. Но для анализа возьмем лишь некоторые из них. После проведенного анализа также станет ясным в надобности проведения многофакторного анализа на эффективность применения БГС [40]. Исходные данные предоставлены в приложении А.4.1. Таблица 3.1.2 – Результаты ассоциативного анализа длины горизонтального участка на добычу нефти на залежи №8 Ромашкинского месторождения
Для связи между двумя группами параметров используется коэффициент ассоциации [37]: А мерой связи будет служить коэффициент сопряженности: Через s обозначим количество групп, различающихся по длине горизонтального участка, через t соответственно группы различающихся по добычи нефти. Но прежде нужно найти величину 2 по формуле [40]: 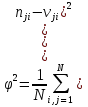 (3.1.3) (3.1.3)В формуле (3.1.3) величина nji обозначает число скважин, попавших в j группу по добычи нефти и в i группу по длине горизонтального участка. Теперь для определения величины 2 необходимо найти значение величины Составим таблицу 3.1.3 с вычисленными результатами величины Таблица 3.1.3 – Вычисленные результаты величины
Далее по формуле (3.1.3) находим, что 2=4,04. Причем это значение должно быть больше Следовательно, связь между длиной горизонтального участка бокового горизонтального ствола и добычей нефти можно считать не случайным. Также стоит рассчитать погрешность данного заявления зависимости длины горизонтального участка от добычи нефти, то есть рассчитать среднеквадратическое отклонение по формуле [40]: По формуле (3.1.2) рассчитаем коэффициент взаимной сопряженности: После проведенного ассоциативного анализа между дебитом нефти и длиной горизонтального участка можно утверждать, что связь между этими параметрами неслучайна, но ввиду немалой величины среднеквадратического отклонения Что касается других параметров, то результаты расчеты приведены в приложении А.4.2. Исходя из результатов расчета, нельзя достаточно достоверно утверждать, что связь между этими параметрами надежна ввиду больших значений погрешности. Но можно утверждать, что связь между этими параметрами неслучайна. После ассоциативного анализа для более точного нахождения среднеквадратического отклонения выполним многофакторный анализ [40]. Для многофакторного анализа выберем три критерия, которые и будем сопоставлять с дебитом нефти, а именно: глубина залегания пласта – фактор А; длина горизонтального участка – фактор В; пластовое давление – фактор С. Таблица 3.1.4 – Данные для многофакторного анализа скважин БГС
Заметим, что не каждая клетка была заполнена. Далее рассчитываем по каждой клетке следующие зависимости [40]: 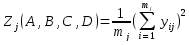 , (3.1.8) , (3.1.8)Таблица 3.1.5 – Распределение
Тогда получаем сумму равную: Далее формируется уже другая таблица 3.1.6, не учитывающая влияния фактора А. Таблица 3.1.6 – Распределение
Также составим подобные таблицы, не учитывающие влияние факторов B и С по очереди. Таблица 3.1.7 - Распределение
Таблица 3.1.8 - Распределение
После составления таблиц без учета того или иного фактора необходимо рассчитать факториальную и остаточную дисперсию по следующим формулам: 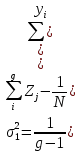 ; (3.1.9) ; (3.1.9)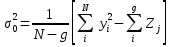 , (3.1.10) , (3.1.10)Но прежде также необходимо составить новые таблицы, которые покажут степень влияния только одного фактора. Таблица 3.1.9 - Распределение
Таблица 3.1.10 - Распределение
Таблица 3.1.11 - Распределение
После вычисления факториальной и остаточной дисперсии необходимо вычислить их отношение, равное: А также число степеней свободы: Далее было необходимо сравнить значения, полученные по формулам (3.1.11), (3.1.12) и (3.1.13) с табличным значениями в таблице 3.1.12. После многофакторного анализа влияния глубины залегания пласта, пластового давления и длины горизонтального участка на дебит нефти выяснилось, что прямой связи между этими параметрами не наблюдается, так как значение Таблица 3.1.12 – Результаты многофакторного анализа на скважинах БГС на залежи №8 Ромашкинского месторождения
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||