Практическая работа по исследований операций. Практическая_Егоровой.А.А_2ПИ. Найти множество Парето следующей двухкритериальной задачи

• Название: Найти множество Парето следующей двухкритериальной задачи
• Анкор: Практическая работа по исследований операций
• Дата: 30.10.2021
• Размер: 231.14 Kb.
• Имя файла: Практическая_Егоровой.А.А_2ПИ.docx
• Тип: Документы; #259406
• страница: 3 из 3

Делим строку 1 на 5/3. Из строк 2, 3, 4 вычитаем строку 1, умноженную на соответствующий элемент в столбце 1.
Вычисляем новые дельты: Δ_i = C₁·a_1i + C₄·a_2i + C₂·a_3i + C₆·a_4i - C_i

Симплекс-таблица с обновлёнными дельтами

C	3	4	0	0	0	0	0
базис	y1	y2	y3	y4	y5	y6	b	Q
y1	1	0	3 5	0	1 5	0	4 5	4 5
y4	0	0	-1	1	1	0	2	2
y2	0	1	1 5	0	2 5	0	3 5	-
y6	0	0	2 5	0	-  6 5	1	36 5	-
Δ	0	0	13 5	0	11 5	0	24 5

Текущий план Y: [4/5,3/5,0,2,0,36/5  ]
Целевая функция F: 3*4/5+4*3/5=24/5


Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.

Ответ: y₁ =  , y₂ =   , F =  

5. Решить задачу линейного программирования симплекс-методом.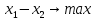



Решение.

Для каждого ограничения с неравенством добавляем дополнительные переменные x₃..x₅.
Перепишем ограничения в каноническом виде:
x₁ + x₂ + x₃ = 2
- 2·x₁ + x₂ + x₄ = 1
3·x₁ - x₂ + x₅ = 3

Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x₃
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x₄
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x₅

Начальная симплекс-таблица

C	1	-1	0	0	0	0
базис	x1	x2	x3	x4	x5	b
x3	1	1	1	0	0	2
x4	-2	1	0	1	0	1
x5	3	-1	0	0	1	3

Вычисляем дельты: Δ_i = C₃·a_1i + C₄·a_2i + C₅·a_3i - C_i

Симплекс-таблица с дельтами

C	1	-1	0	0	0	0
базис	x1	x2	x3	x4	x5	b
x3	1	1	1	0	0	2
x4	-2	1	0	1	0	1
x5	3	-1	0	0	1	3
Δ	-1	1	0	0	0	0

Проверяем план на оптимальность: план не оптимален, так как Δ₁ = -1 отрицательна.

Итерация 1

Определяем разрешающий столбец - столбец, в котором находится минимальная дельта: 1, Δ₁: -1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения столбца 1
В найденном столбце ищем строку с наименьшим значением Q: Q_min = 1, строка 3.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x₅ берём x₁.

C	1	-1	0	0	0	0
базис	x1	x2	x3	x4	x5	b	Q
x3	1	1	1	0	0	2	2 / 1 = 2
x4	-2	1	0	1	0	1	-
x1	3	-1	0	0	1	3	3 / 3 = 1
Δ	-1	1	0	0	0	0

Делим строку 3 на 3. Из строк 1, 2 вычитаем строку 3, умноженную на соответствующий элемент в столбце 1.
Вычисляем новые дельты: Δ_i = C₃·a_1i + C₄·a_2i + C₁·a_3i - C_i

Симплекс-таблица с обновлёнными дельтами

C	1	-1	0	0	0	0
базис	x1	x2	x3	x4	x5	b	Q
x3	0	4 3	1	0	-  1 3	1	2
x4	0	1 3	0	1	2 3	3	-
x1	1	-  1 3	0	0	1 3	1	1
Δ	0	2 3	0	0	1 3	1

Текущий план X: [ 1, 0, 1, 3, 0 ]
Целевая функция F: 1·1 + -1·0 + 0·1 + 0·3 + 0·0 = 1
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.

Ответ: x₁ = 1, x₂ = 0, F = 1