9 Центральная предельная теорема. Неравенство Чебышева

• Название: Неравенство Чебышева
• Дата: 22.04.2023
• Размер: 69.69 Kb.
• Имя файла: 9 Центральная предельная теорема.docx
• Тип: Лекция; #1080508
• страница: 1 из 5

ЛЕКЦИЯ9: Центральная предельная теорема

1. Неравенство Чебышева

Как уже неоднократно отмечалось, наличие закономерностей в случай- ных явлениях обусловлено их массовостью. Только при большом количестве опытов или объектов исследования проявляются закономерности в устойчиво- сти некоторых средних характеристик. Например, при большом числе бросков монеты, число выпадения решки к общему числу бросков будет стремиться к значению 0,5. Устойчивость средних характеристик и составляет закон боль- ших чисел. Суть его заключается в следующем: при очень большом числе слу- чайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью точности. Под законом больших чисел понимают целый ряд теорем, где устанавливается при различных услови- ях опыта, факт приближения средних характеристик к некоторым постоянным при увеличении числа этих опытов.

НеравенствоЧебышева(лемма). Пусть имеется случайная величина X

с характеристиками m_x и

D_x. Каково бы ни было

  0, вероятность того, что

случайная величина X отклонится от своего математического ожидания не

меньше чем на  ограничено сверху величиной

D<sub>x,

</sub>2

x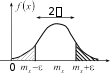
P x m

   ^Dx.

_2

Действительно, допустим для непре- рывной случайной величины X распреде-

ленной по закону fx, следует

m_x 


x
P x m    _ fxdx_.

m_x

Рассмотрим определение дисперсии

D_x



_x m_x



² fxdx _

10. 
     m_x
    

² fxdx

 

 _ 

m_x _




 ² _ fxdx  ^{2 } _ fxdx

_ fxdx^  ²

_ fxdx.

 _ m_x

 _

xm_x

Отсюда непосредственно следует

fxdx  <sup>Dx


</sup> 2

x


или

P x m

  ^Dx

_2

. что

xm_x

и требовалось показать. Иногда удобно перейти к противоположному событию

x
P x m

 1  ^Dx.

_2

Заметим, что неравенство Чебышева имеет большое теоретическое зна- чение, так как позволяет достаточно просто доказать целый ряд теорем закона больших чисел. С другой стороны, неравенство Чебышева не имеет большого практического приложения, поскольку точность оценок, сделанных на основе его применения, невелика. Например, оценим вероятность отклонения случай-

ной величины, распределенной по нормальному закону, на

3_x

от m_x. Нера-

венство Чебышева дает

P x m

 3 

D_x


x

x
9²

 0,1, тогда как на самом деле

x
P x m

• 
  _x
  

  Ф3  Ф0  0,003 . Таким образом, неравенство Чебышева

дает только грубую оценку.