9 Центральная предельная теорема. Неравенство Чебышева

• Название: Неравенство Чебышева
• Дата: 22.04.2023
• Размер: 69.69 Kb.
• Имя файла: 9 Центральная предельная теорема.docx
• Тип: Лекция; #1080508
• страница: 2 из 5

Закон больших чисел

Пусть производится n независимых опытов в равных условиях. В ре- зультате этих опытов случайная величина X принимает различные значения

x₁ , x₂ , x₃ ,, x_n. Предположим, что все x_i распределены по одному закону


i x
распределения Mx  mи Dx_i  D_x, i 1, n. Введем новую случайную вели-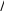

n

чину

Y _ x_i n

1

и получим ее математическое ожидание и дисперсию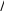

n

n
m MY  M^_n xn^  ¹ _n Mx  ^nmx m,

y _ i _ i x





1 1

D DY D^_n x

_n _ ¹ _ⁿ

Dx ^nDx ^Dx.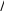


y _ i

1

_ _n2 ₁

ⁱ n² n

Видно, что при

n,

D_y 0 . То, есть случайная величина Yуже не явля-

ется случайной. Чем больше будет опытов, тем точнее можно определить зна-


x
чение Y, MY m.
Теорема Чебышева. При достаточно большом числе независимых опы- тов среднее арифметическое наблюдаемых значений случайной величины схо- дится по вероятности к ее математическому ожиданию



_P n _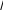

Ym_xили P^ _ x_in m_x  ^  1   ,

  0,

  0 .

 ¹ 

Доказательство. Применим неравенство Чебышева:

PY m

  следует P ^ _ x_i

n m_x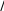


 ^    .

_{Dy } n


2

y
 _{ 1}

^ D<sub>x

</sub> n

Каково бы не было число , всегда найдется число n, которое дает

  ^Dx

n²

1

 ⁿ 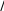

, где значение D_x ограничено. Таким образом,

P ^ _ x_i n m_x  ^  1  ,

что и требовалось доказать.

 ¹ 

Заметим, что Марков обобщил эту теорему на зависимые опыты и нерав- новероятные опыты. Было сделано обобщение теоремы Чебышева и на случай переменных условий опыта.

Заметим так же, что до теоремы Чебышева, основанием закона больших чисел была теорема Бернулли, с громоздким выводом. Приведем доказатель- ство теоремы Бернулли с использованием неравенства Чебышева.

Теорема Бернулли. При неограниченном увеличении числа независимых опытов, частота события Aсходится по вероятности к его вероятности

PA  Pв отдельном опыте.

Доказательство. Пусть

x₁ – число появления события Aв одном опыте,

x₂ – во втором опыте и так далее. Наконец x_n– число появлений события в n-

0	1
q	P

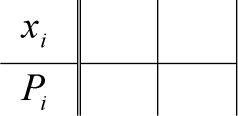ом опыте. Закон распределения X–

где P q1, тогда m_x 0  q 1 P P ^,


x
D 0²  q 1²  P P²  P1  P  Pq. Ча-

стота события Aопределяется

^*  ^m* 




n

P
n ₁

10. 
    n. Тогда
    

MP

^*  ¹ n



n₁

Mx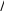

i
 m, DP^* ¹ _Dx ^Dx.

n




^x 2 ⁱ


n

n
1

Используя неравенство Чебышева, получаем

PP^*  P  1 

^Dx 1

n²

для

n.

Пример. Стрелок стреляет в мишень 300 раз, причем вероятность его по-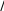

падания в мишень при каждом выстреле равна 2 3 . Оценить вероятность попа-

дание в мишень от 185 до 215 раз

^ P^*  _n xn^ .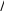





i
 1 

Решение.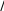

_ 300

m_p 2 3 ,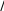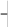

2

 15 300  0,05 . Тогда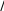

^ 2  300²

D_x P q1 3  2 3  2 9 и

P^ _ x_i

300 

3

 0,05^  1 

9  300 15²

 1  0,3  0,7 .

 ¹ 