9 Центральная предельная теорема. Неравенство Чебышева

• Название: Неравенство Чебышева
• Дата: 22.04.2023
• Размер: 69.69 Kb.
• Имя файла: 9 Центральная предельная теорема.docx
• Тип: Лекция; #1080508
• страница: 3 из 5

Центральная предельная теорема

В законе больших, чисел мы рассматривали предельные значения самих

случайных величин. Теперь рассмотрим предельные законы законов распреде- ления случайных величин. Основная идея продельной теоремы состоит в том, что при суммировании достаточно большого числа случайных величин распре- деление суммы случайных величин стремится к нормальному закону. И чем больше членов в сумме, тем точнее она будет описываться нормальным зако- ном распределения. При этом не играет роли, как распределены сами члены суммы.

Перечислим требования, предъявляемые к сумме случайных величин: во-

первых, члены суммы должны быть одного порядка малости (равномерно ма- лыми) и, во-вторых, сумма должна состоять из достаточно большого числа сла-

гаемых n 20. Отметим, что центральная предельная теорема на самом де-

ле – это целый комплекс теорем для различных условий опыта. Приведем са- мую простую из них.

Теорема. Если

x₁ , x₂ , x₃ ,, x_n

– независимые случайные величины,

имеющие один и тот же закон распределения с математическим ожиданием m

и дисперсией ² , то при неограниченном возрастании числа случайных вели-

n

чин n, закон распределения их суммы

Y _ x_i

1

c m_y nm и

D_y nD

y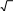
 

n

неограниченно приближается к нормальному

ym_y ²

fy 

_{1 e}

2²


y
.

и вероятность, что случайная величина Y попадет в интервал ,

приближенно равна

будет

^   m_y^{ }   m_y^





P  Y   Ф^  Ф^ ,

где
m_y nm
и  _y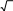
n .

 

 ^y 

 

 ^y 