9 Центральная предельная теорема. Неравенство Чебышева

• Название: Неравенство Чебышева
• Дата: 22.04.2023
• Размер: 69.69 Kb.
• Имя файла: 9 Центральная предельная теорема.docx
• Тип: Лекция; #1080508
• страница: 4 из 5

Характеристические функции и их свойства

Отметим, что частным случаем центральной предельной теоремы являет-

ся нелокальная теорема Муавра-Лапласа (смотрите лекцию 3) с P_nm 


n
_{ C}m_Pm_qnm_,


y

y
m_y nP, D nPq,   nPq. Вероятность попадания Y в ,:

^   nP^{ }   nP^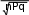

P  Y   Ф^

 _{ Ф}

^ была нами получена ранее.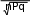

   

Доказательство.Введем понятие характеристической функции (Ляпунов)

gt  Me^itx – здесь Xслучайная величина. Например, для дискретной слу-

чайной величины с законом распределения:

xi	x1	x2		xn
Pi	P1	P2		Pn

, gt  _

k1

_eitx_kP,

k


для непрерывной случайной величины

gt 

_ fxe^itxdx



является ни чем

иным как преобразованием Фурье. Отметим, что

lim gt  1.Заметим также,

t0

что можно ввести комплексную случайную величину

Z X iY, как пару

случайных величин. Очевидно, что для нее должно выполняться соотношения

MZ MX iMY, DZ  DX DY, DZ 0 .

Найдем характеристическую функцию нормального закона распределе-

ния с параметрами Тогда

m_x 0 ,

_x  1,

fx

1 ^{ x}2


2


e ,

2

_
 _ x² _ 

_ ACB² _{ }t²

gt 

_{e 2 e}itx_dx ^ _eAx² 2 BxC_dx

 _

e ^{A }  e ² .



_
Исходя из определения характеристической функции, перечислим ее

основные свойства:

- lim gt  1;

t0

-если y ax, то g_yt  g_xat;

n n

-если

x_iнезависимые и

Y _ x_i, то

1

g_yt  _ g_xt.

1

Далее, используем первое свойство

t 0:

gt, разложим ее в ряд Маклорена при

gt  g0  g^ 0 t g^ 0 t²  ,

где

g_x0 1,

x x

g^_x0  im_x 0 ,

x

g^_x0  

x

x
² . Тогда

g_xt  1

_2

_x_t2 _.

2

Используем третье свойство

gt. Для суммы случайных величин Yха-

рактеристическая функция будет иметь вид

gt  gtⁿ. Получаем в преде-

y x
  n

 ² n

_2_t2


ле n,

g_yt 

_1 



2

x_t2

2 _

 _1 



y_{t2 }

2n <sub>

</sub>y

 e ²
_t2


. Если обезразмерить слу-

чайную величину Y,

Z y _y

то g_Zt  e ² .

Таким образом, сумма случайных величин но, распределена по нормальному закону.