4 розд моног 2014. Обрунтування та аналіз математичних моделей симетричних блокових перетворень
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
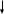
Рис. 4.3 Заповнення внутрішнього стану 4.3.4 Алгоритм зашифрування в базовому режимі Структура перетворення. Базове перетворення зашифрування 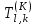 визначено у такому вигляді [3-4]: визначено у такому вигляді [3-4]: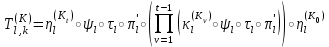 , ( 4.23) , ( 4.23)Де: 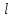 – розмір внутрішнього стану блокового шифру у бітах; – розмір внутрішнього стану блокового шифру у бітах;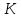 – ключ зашифрування; – ключ зашифрування;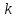 – довжина ключа шифрування у бітах; – довжина ключа шифрування у бітах;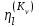 – функція додавання циклового ключа – функція додавання циклового ключа 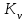 ( (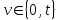 ) за модулем 264; ) за модулем 264; 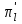 – шар нелінійного бієктивного відображення, який виконує обробку векторів, що задані над – шар нелінійного бієктивного відображення, який виконує обробку векторів, що задані над 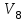 (байтова підстановка); (байтова підстановка);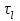 – перестановка елементів – перестановка елементів 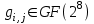 внутрішнього стану (циклічний зсув рядків вправо при матричному поданні); внутрішнього стану (циклічний зсув рядків вправо при матричному поданні);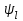 – лінійне перетворення, що здійснюється засобом множення матриці лінійного перетворення на матрицю внутрішнього стану над скінченним полем; – лінійне перетворення, що здійснюється засобом множення матриці лінійного перетворення на матрицю внутрішнього стану над скінченним полем;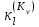 – функція додавання циклового ключа – функція додавання циклового ключа 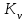 ( (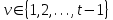 ) за модулем 2 , яа реалізує інволютивне перетворення. ) за модулем 2 , яа реалізує інволютивне перетворення.В функціях 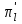 , , 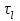 і і 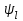 вхідний аргумент вхідний аргумент 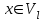 та вихідне значення та вихідне значення 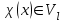 , , 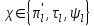 розглядаються як матриці розміром розглядаються як матриці розміром 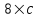 байтів згідно таблиці 4.3. байтів згідно таблиці 4.3.Функції 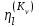 і і 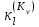 мають два вхідних аргументи мають два вхідних аргументи 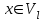 (внутрішній стан шифру) і (внутрішній стан шифру) і 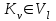 (цикловий ключ (цикловий ключ 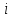 -ї ітерації) та вихідне значення -ї ітерації) та вихідне значення 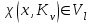 , , 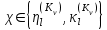 , при цьому вхідні аргументи та вихідне значення розглядаються як матриці розміром , при цьому вхідні аргументи та вихідне значення розглядаються як матриці розміром 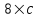 байтів. байтів.Функція додавання циклового ключа 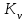 за модулем 264. за модулем 264. 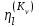 здійснює додавання за модулем 264 стовпців матриці внутрішнього стану здійснює додавання за модулем 264 стовпців матриці внутрішнього стану 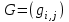 і стовпців матриці циклового ключа і стовпців матриці циклового ключа 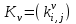 , при цьому результат також є матрицею розміром , при цьому результат також є матрицею розміром 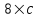 байтів, тобто внутрішнім станом після додавання ключа. При чому при додаванні найменш значущі байти мають менший індекс, тобто використовується формат little endian[ ]. байтів, тобто внутрішнім станом після додавання ключа. При чому при додаванні найменш значущі байти мають менший індекс, тобто використовується формат little endian[ ].Шар нелінійного бієктивного відображення. Функція 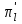 виконує заміну кожного елементу виконує заміну кожного елементу 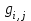 матриці внутрішнього стану матриці внутрішнього стану 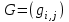 на на 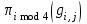 , де , де 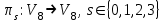 - засобом застосування випадкової підстановки[4]. - засобом застосування випадкової підстановки[4]. Наприклад, нехай 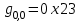 , тоді , тоді 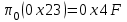 . .Перестановка елементів. Функція 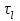 виконує циклічний зсув вправо рядків матриці стану виконує циклічний зсув вправо рядків матриці стану 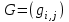 . Кількість елементів зсуву залежить від номеру рядку . Кількість елементів зсуву залежить від номеру рядку 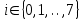 , розміру блоку , розміру блоку 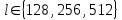 , та обчислюється за формулою , та обчислюється за формулою 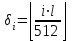 . .Наприклад, 5-й рядок матриці стану шифру з 256-бітовим блоком зсувається вправо на 2 елемента. Лінійне перетворення. При обчисленні результату функції 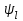 кожен елемент кожен елемент 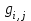 матриці внутрішнього стану матриці внутрішнього стану 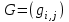 розглядається як елемент скінченного поля розглядається як елемент скінченного поля 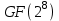 , що утворене незвідним поліномом , що утворене незвідним поліномом 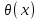 = x8 + x4 + x3 + x2 + 1, або 0х11d у шістнадцятковому поданні. = x8 + x4 + x3 + x2 + 1, або 0х11d у шістнадцятковому поданні.Кожен елемент результуючої матриці стану 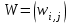 отримується як результат множення векторів довжини 8 над скінченним полем отримується як результат множення векторів довжини 8 над скінченним полем 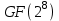 згідно формули [ ] згідно формули [ ]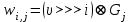 , (4.24) , (4.24)де 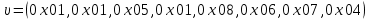 – вектор, що утворює циркулянтну матрицю МДР - коду і складається з послідовності байтових констант у шістнадцятковому поданні, які інтерпретуються як елементи поля – вектор, що утворює циркулянтну матрицю МДР - коду і складається з послідовності байтових констант у шістнадцятковому поданні, які інтерпретуються як елементи поля 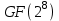 , при цьому циклічний зсув виконується відносно елементів вектора над скінченним полем[ ] ; , при цьому циклічний зсув виконується відносно елементів вектора над скінченним полем[ ] ;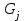 – –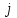 –й стовпець матриці стану –й стовпець матриці стану 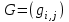 . .Функція додавання циклового ключа 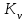 за модулем 2. Функція за модулем 2. Функція 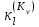 має два вхідних аргументи: має два вхідних аргументи: 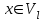 (внутрішній стан шифру) і (внутрішній стан шифру) і 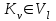 (цикловий ключ (цикловий ключ 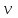 -ї ітерації), кожен з яких поданий як матриця розміром -ї ітерації), кожен з яких поданий як матриця розміром 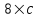 байтів. байтів.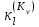 здійснює побітове додавання (за модулем 2) стовпців матриці внутрішнього стану здійснює побітове додавання (за модулем 2) стовпців матриці внутрішнього стану 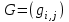 і стовпців матриці циклового ключа і стовпців матриці циклового ключа 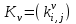 , при цьому результат також є матрицею розміром , при цьому результат також є матрицею розміром 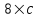 байтів (внутрішнім станом після додавання). байтів (внутрішнім станом після додавання).4.3.5 алгоритм розшифрування в базовому режимі. Базове перетворення розшифрування. Базове перетворення розшифрування 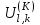 визначено наступним чином: визначено наступним чином: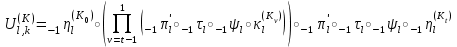 , (4.25) , (4.25)де: 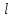 – розмір внутрішнього стану блокового шифру (у бітах); – розмір внутрішнього стану блокового шифру (у бітах);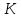 – ключ шифрування; – ключ шифрування;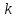 – довжина ключа шифрування (у бітах); – довжина ключа шифрування (у бітах);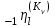 – функція віднімання циклового ключа – функція віднімання циклового ключа 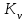 ( (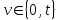 ) за модулем 264 (зворотна до ) за модулем 264 (зворотна до 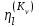 ); ); 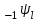 – зворотне лінійне перетворення (множення матриці зворотного лінійного перетворення на матрицю внутрішнього стану над скінченним полем); – зворотне лінійне перетворення (множення матриці зворотного лінійного перетворення на матрицю внутрішнього стану над скінченним полем);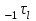 – зворотна перестановка елементів – зворотна перестановка елементів 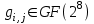 внутрішнього стану (циклічний зсув рядків вліво при матричному поданні); внутрішнього стану (циклічний зсув рядків вліво при матричному поданні);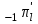 – шар зворотного нелінійного бієктивного відображення, який виконує обробку векторів, заданих над – шар зворотного нелінійного бієктивного відображення, який виконує обробку векторів, заданих над 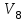 (зворотна байтова підстановка); (зворотна байтова підстановка);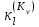 – інволютивна функція додавання циклового ключа – інволютивна функція додавання циклового ключа 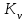 ( (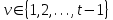 ) за модулем 2 (однакова для зашифрування і розшифрування). ) за модулем 2 (однакова для зашифрування і розшифрування).Як і при зашифруванні при розшифруванні , в функціях 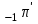 , , 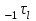 і і 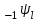 вхідний аргумент вхідний аргумент 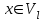 та вихідне значення та вихідне значення 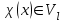 , , 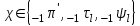 розглядаються як матриці розміром розглядаються як матриці розміром 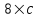 байтів. байтів.Функція 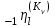 має два вхідних аргументи має два вхідних аргументи 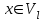 (внутрішній стан шифру) і (внутрішній стан шифру) і 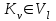 (цикловий ключ (цикловий ключ 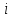 -ї ітерації) та вихідне значення -ї ітерації) та вихідне значення 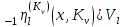 , при цьому вхідні аргументи та вихідне значення розглядаються як матриці розміром , при цьому вхідні аргументи та вихідне значення розглядаються як матриці розміром 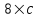 байтів. байтів.Функція віднімання циклового ключа 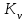 за модулем 264. за модулем 264. 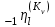 є зворотною до є зворотною до 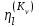 і здійснює віднімання за модулем 264 стовпців матриці циклового ключа і здійснює віднімання за модулем 264 стовпців матриці циклового ключа 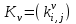 від стовпців матриці внутрішнього стану від стовпців матриці внутрішнього стану 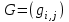 , при цьому результат також є матрицею розміром , при цьому результат також є матрицею розміром 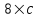 байтів (внутрішнім станом після віднімання[3-4]. байтів (внутрішнім станом після віднімання[3-4].При виконанні віднімання найменш значущі байти мають менший індекс, тобто використовується формат little endian[ ]. Шар зворотного нелінійного бієктивного відображення. Функція 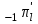 виконує заміну кожного елементу виконує заміну кожного елементу 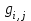 матриці внутрішнього стану матриці внутрішнього стану 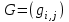 на на 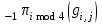 , де , де 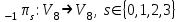 - підстановки, які наведені у додатку А[ ]. - підстановки, які наведені у додатку А[ ]. Наприклад, нехай 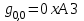 , тоді , тоді 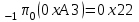 . .Зворотна перестановка елементів. Функція 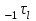 виконує циклічний зсув вліво рядків матриці стану виконує циклічний зсув вліво рядків матриці стану 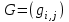 . Кількість елементів зсуву залежить від номеру рядку . Кількість елементів зсуву залежить від номеру рядку 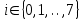 розміру блоку розміру блоку 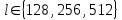 , та обчислюється за формулою , та обчислюється за формулою | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
