ТЕСТ
Какая из приведённых пар волн является когерентной?
а) 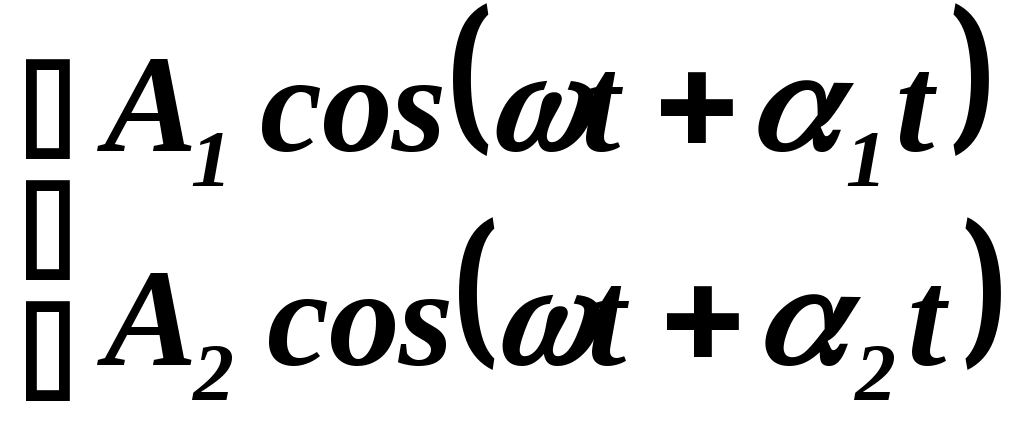 ; б) ; б) 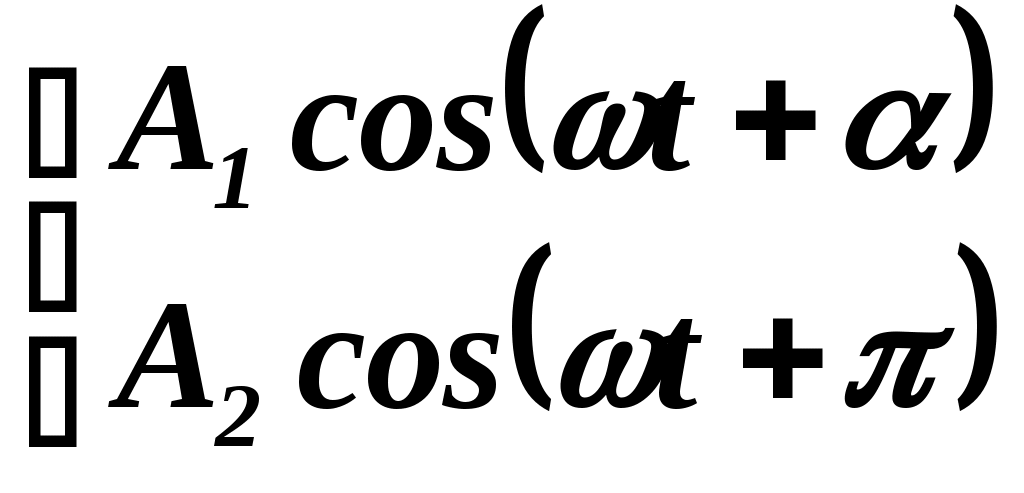 ; в) ; в)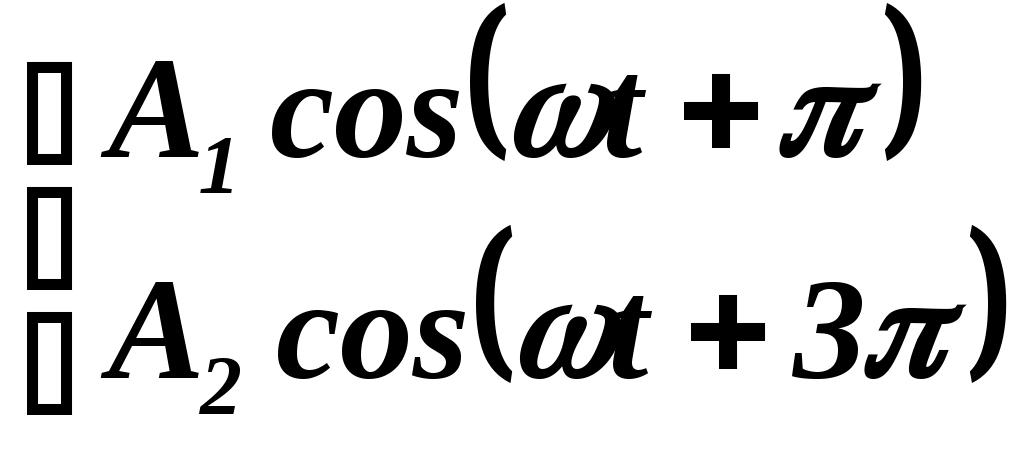 . .
Чему равна интенсивность (I) света, полученного при сложении когерентных волн 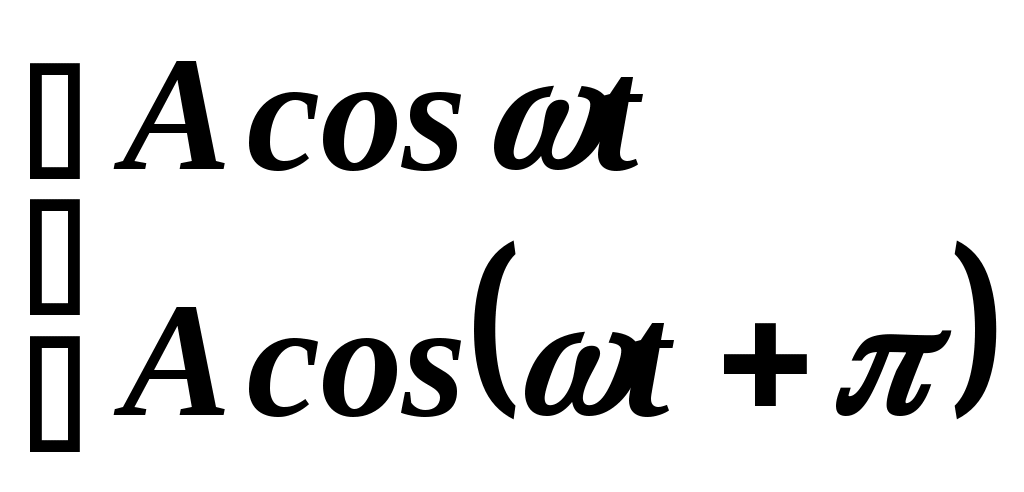 ? ?
а) 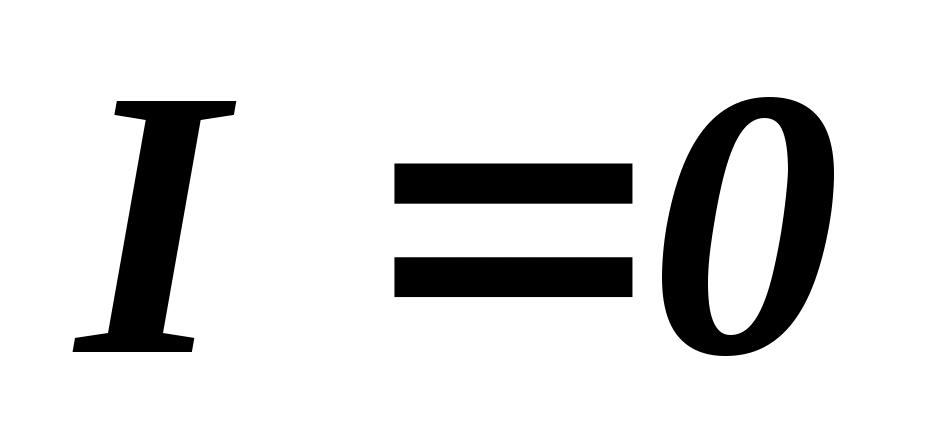 ; б) ; б) 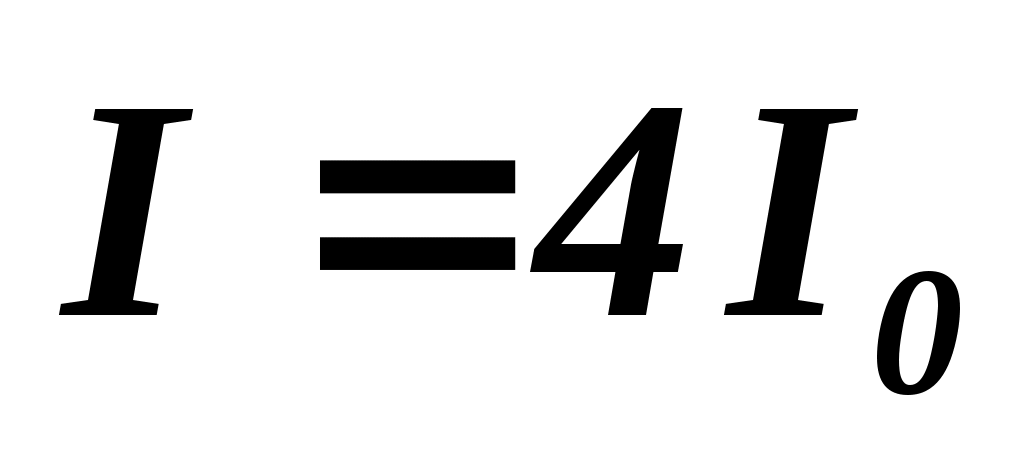 ; в) ; в) 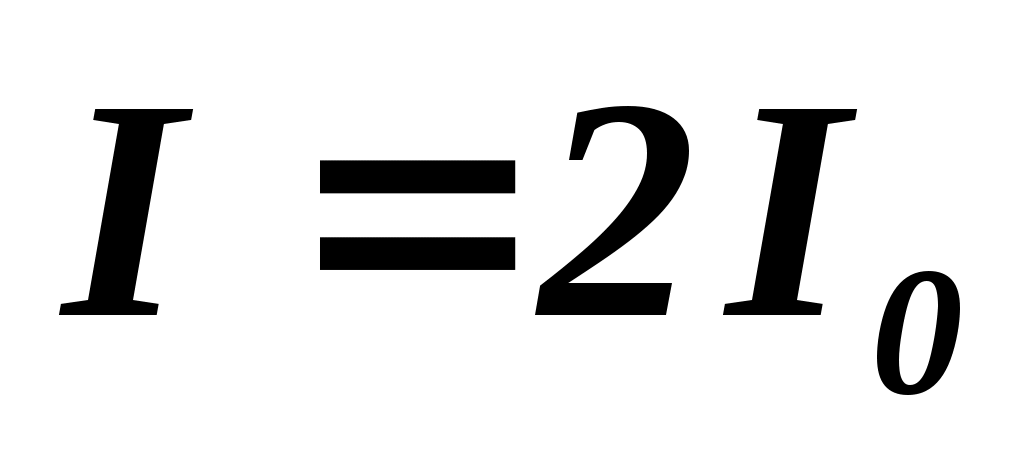 . .
Чему равна интенсивность (I) света, полученного при сложении когерентных волн 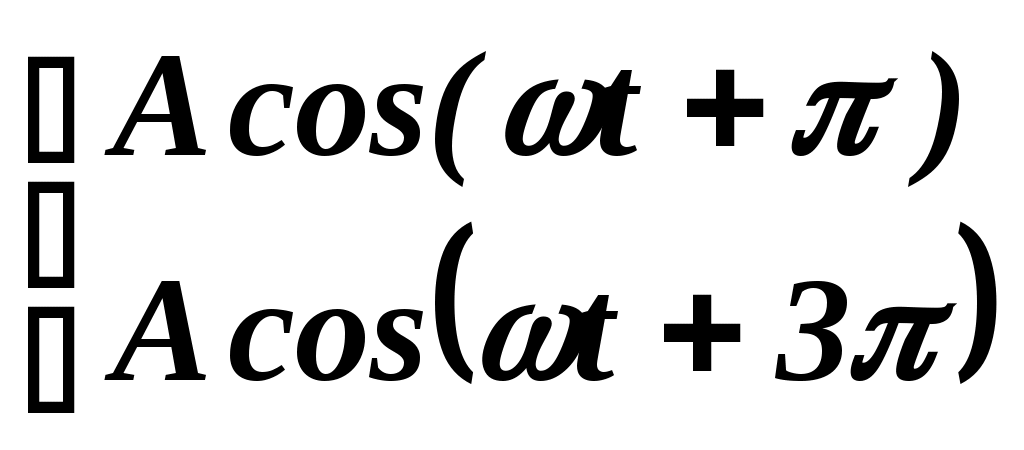 ? ?
а) 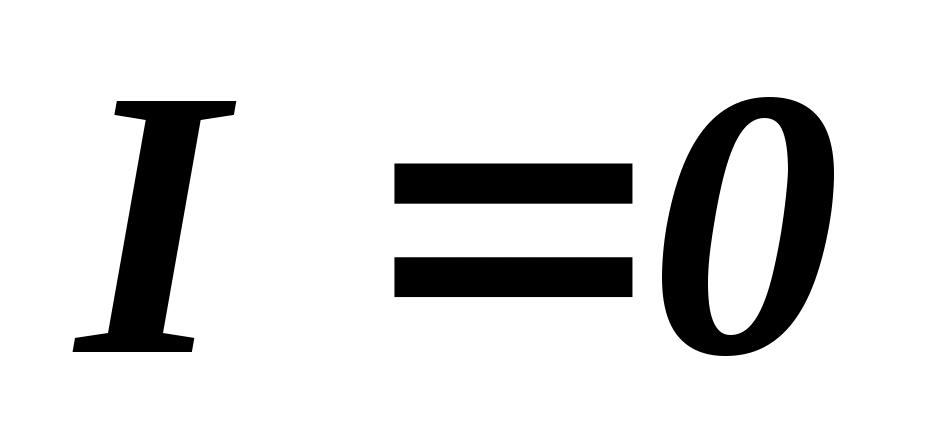 ; б) ; б) 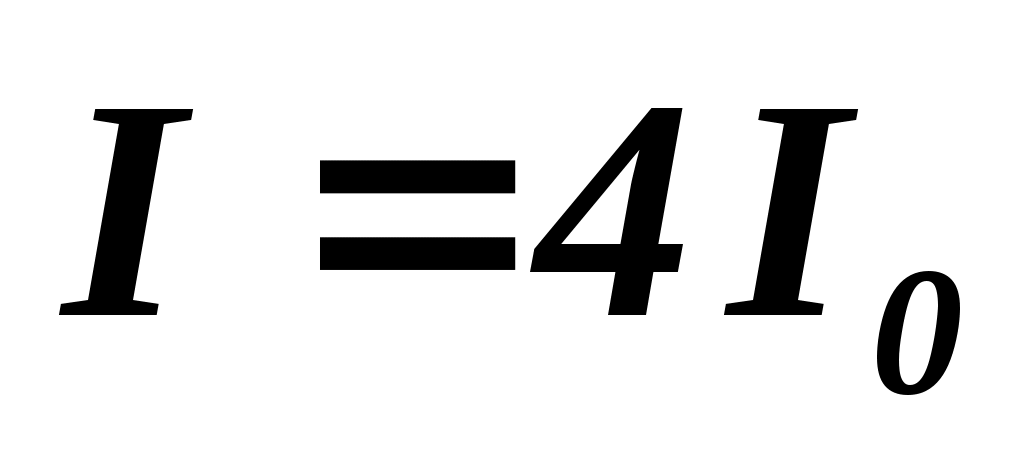 ; в) ; в) 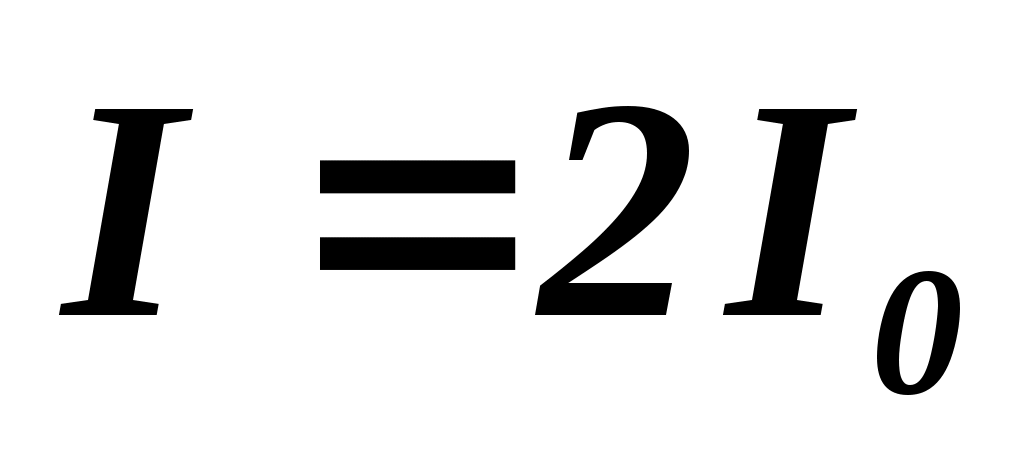 . .
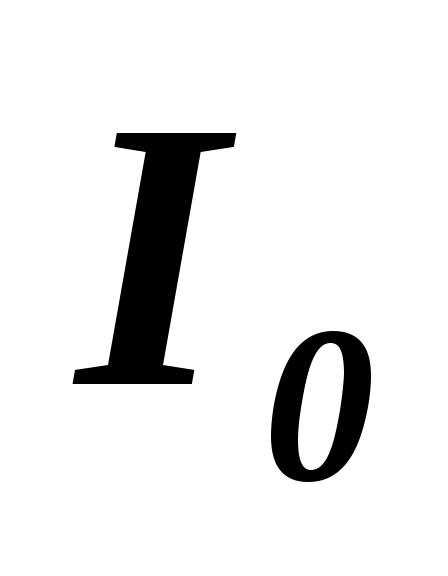 – интенсивность каждой когерентной волны. – интенсивность каждой когерентной волны.
Какие из перечисленных источников являются когерентными?
а) Две раскаленные линии.
б) Лазерный луч.
в) Солнечные лучи, прошедшие через призму.
г) Лучи, полученные при прохождении через бипризму Френеля.
Как зависит ширина интерференционной зоны от преломляющего угла бипризмы?
а) Чем больше угол  , тем шире зона интерференции. , тем шире зона интерференции.
б) Чем меньше угол  , тем шире зона интерференции. , тем шире зона интерференции.
в) Ширина зон интерференции не зависит от величины угла  . .
ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ С ПОМОЩЬЮ ЛАЗЕРА
(Лабораторная работа 78)
Цель работы: изучить явление дифракции света.
Явление дифракции света заключается в отклонении световых волн от прямолинейного пути при огибании светом малых препятствий в оптически однородной среде.
Дифракция характерна для волнового процесса. Выделяют два случая дифракции: дифракцию сферических световых волн (дифракцию Френеля), которая наблюдается при конечном расстоянии преграды от экрана; дифракцию в параллельных лучах (дифракцию Фраунгофера) для плоских световых волн. Во втором случае дифракция наблюдается только с помощью линзы, собирающей лучи в фокальной плоскости, или глазом, аккомодированным на бесконечность.
В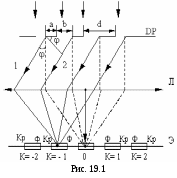 основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны. основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны.
Принцип Гюйгенса-Френеля рассматривает интенсивность результирующей волны как результат интерференции вторичных волн.
Рассмотрим дифракцию света при прохождении через дифракционную решетку (рис. 19.1).
Простейшая дифракционная решётка представляет собой стеклянную пластинку, на которую нанесены параллельные друг другу царапины, а между ними оставлены узкие неповрежденные полоски, то есть дифракционная решетка – это система одинаковых щелей.
Сумма размеров прозрачной (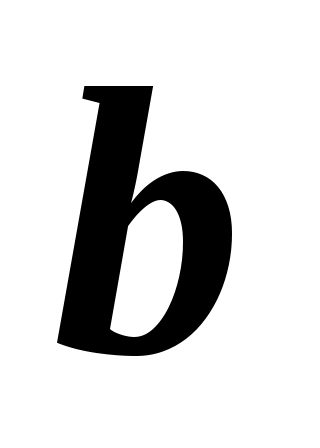 ) и непрозрачной ( ) и непрозрачной ( ) полос называется периодом, или постоянной решетки ( ) полос называется периодом, или постоянной решетки ( ) (рис. 19.1): ) (рис. 19.1):
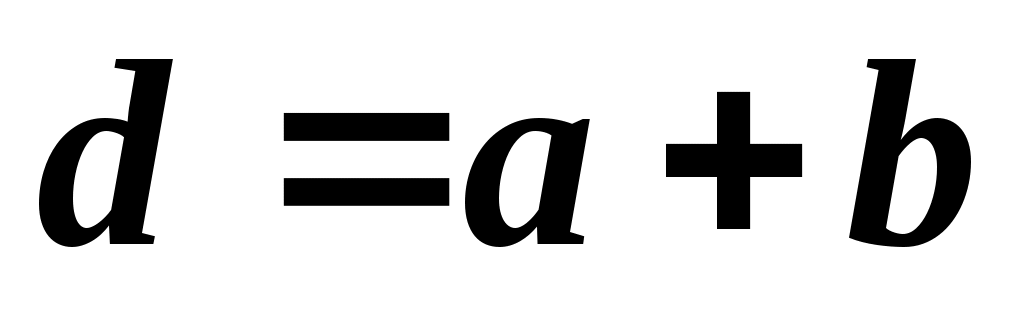 . .
Свет, проходя через узкие щели решетки, испытывает дифракцию, то есть отклоняется от первоначального направления. Дифрагирующие лучи от отдельных щелей налагаются друг на друга в фокальной плоскости линзы и интерферируют между собой. Если число щелей равно 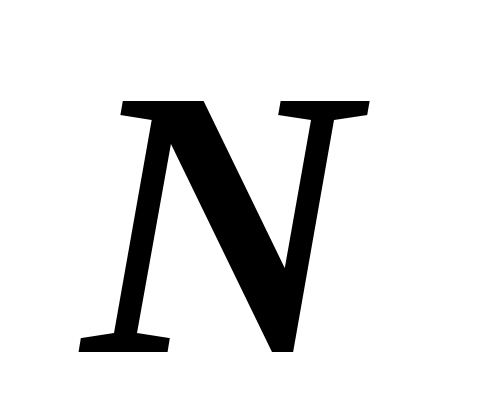 , то интерферируют между собой , то интерферируют между собой 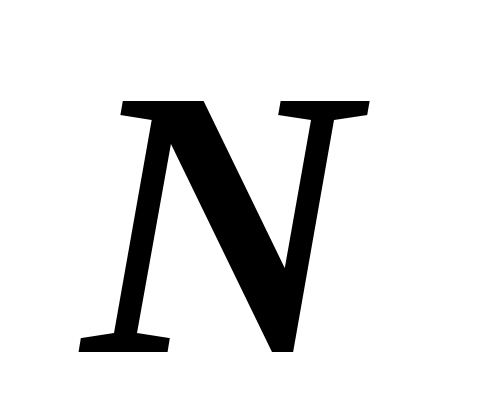 пучков. пучков.
Пусть свет с длиной волны  падает на решетку падает на решетку  нормально (см. рис. 19.1).За щелями в результате дифракции лучи будут распространяться по различным направлениям. Рассмотрим лучи, составляющие угол нормально (см. рис. 19.1).За щелями в результате дифракции лучи будут распространяться по различным направлениям. Рассмотрим лучи, составляющие угол  с нормалью к решетке. Разность хода между лучами I и 2 с нормалью к решетке. Разность хода между лучами I и 2 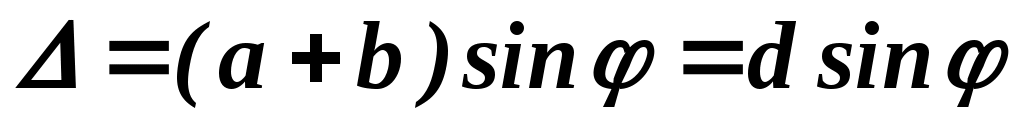 . Этой разности хода соответствует разность фаз: . Этой разности хода соответствует разность фаз:
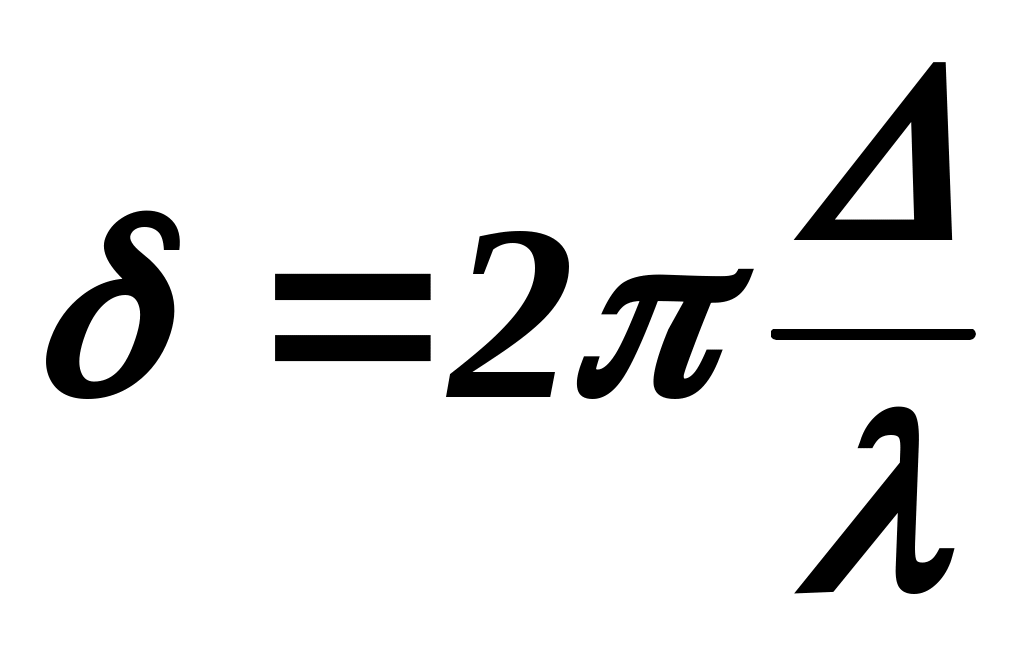 . .
Если 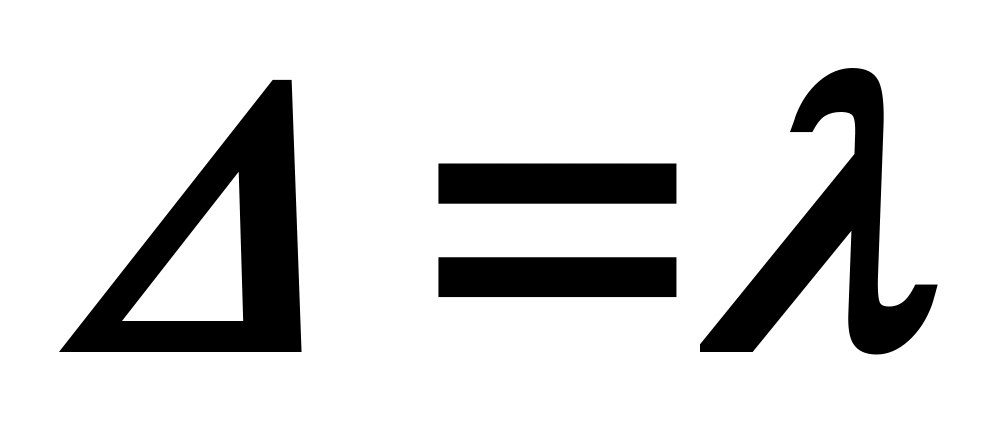 , то , то 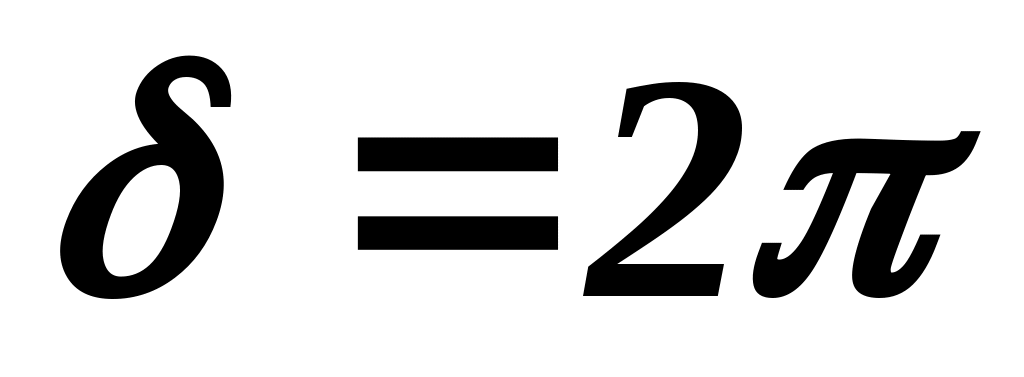 , то есть лучи I и 2 приходят на экран в одинаковых фазах и усиливают друг друга. Условие образования максимумов в общем случае имеет вид: , то есть лучи I и 2 приходят на экран в одинаковых фазах и усиливают друг друга. Условие образования максимумов в общем случае имеет вид:
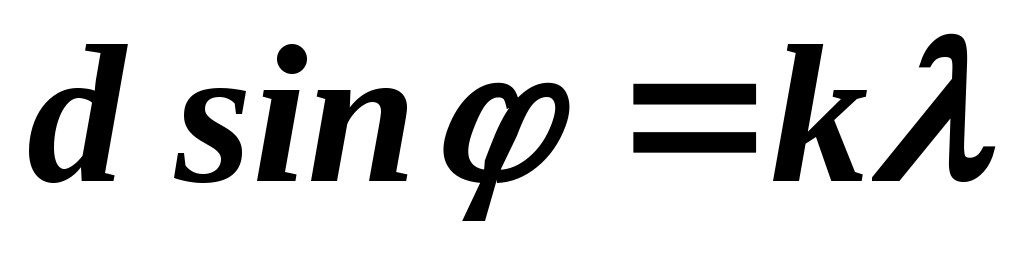 , (19.1) , (19.1)
где 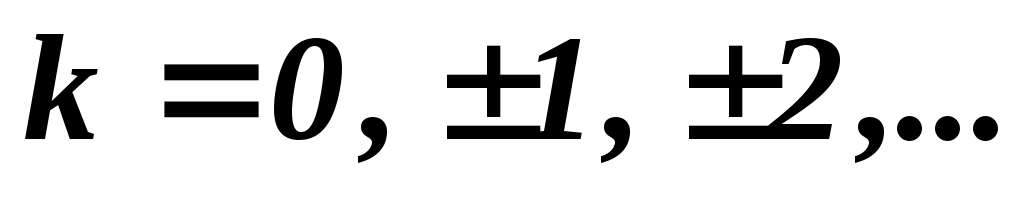
Условие (19.1) определяет положение главных максимумов.
Положение минимумов определяется условием:
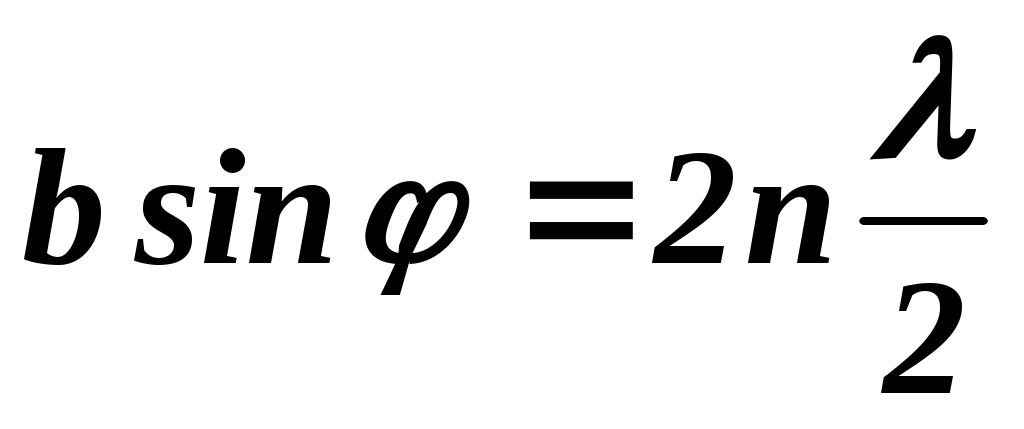 , ,
где 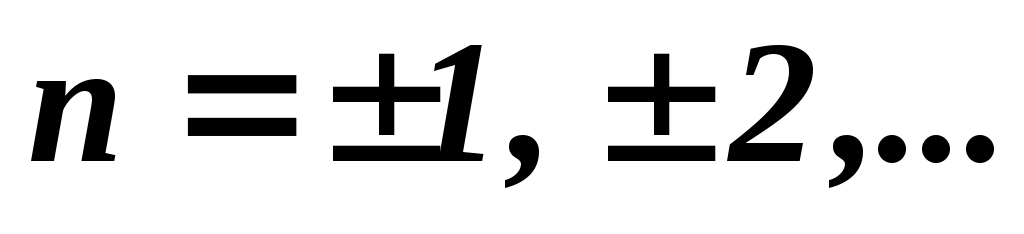
Причем эти минимумы получаются там же, где были минимумы от одной щели.
Добавочные минимумы определяются соотношением:
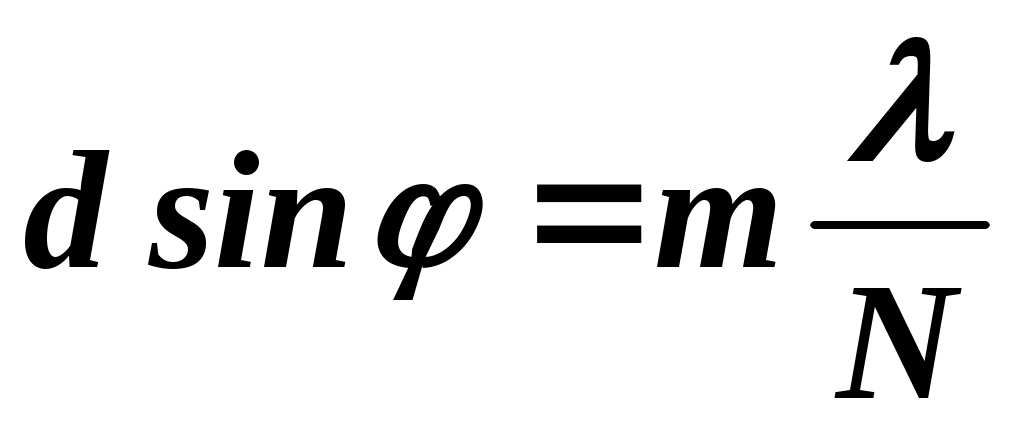 , ,
где 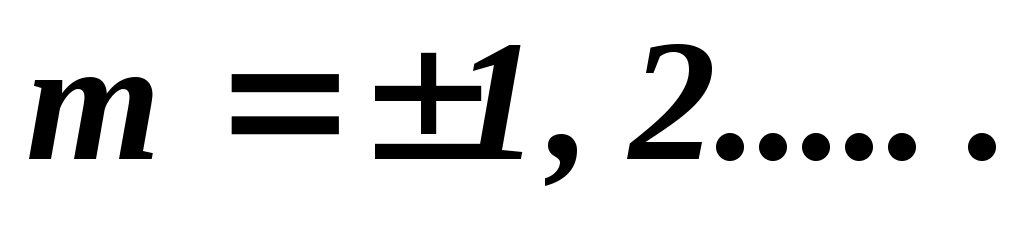 , N – число щелей решетки. , N – число щелей решетки.
М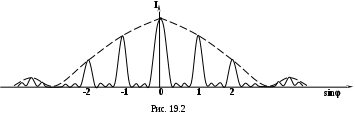
ежду двумя главными максимумами располагается 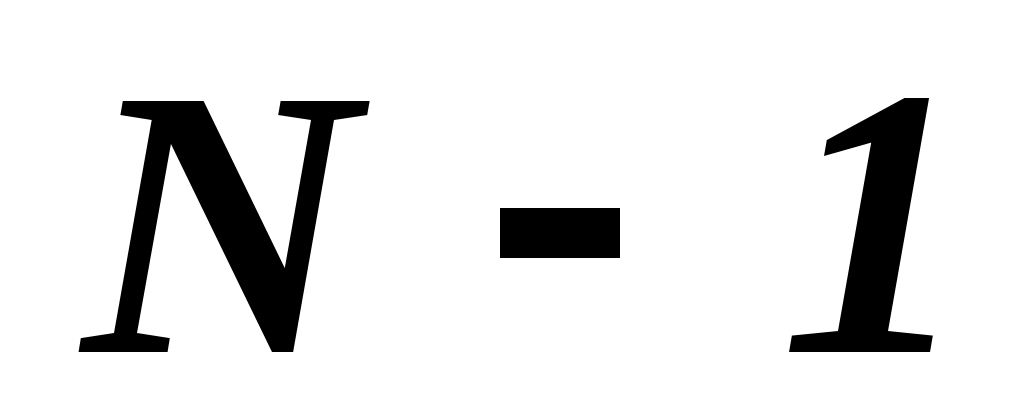 добавочных минимумов, разделенных вторичными максимумами (рис. 19.2). Интенсивность главных максимумов добавочных минимумов, разделенных вторичными максимумами (рис. 19.2). Интенсивность главных максимумов 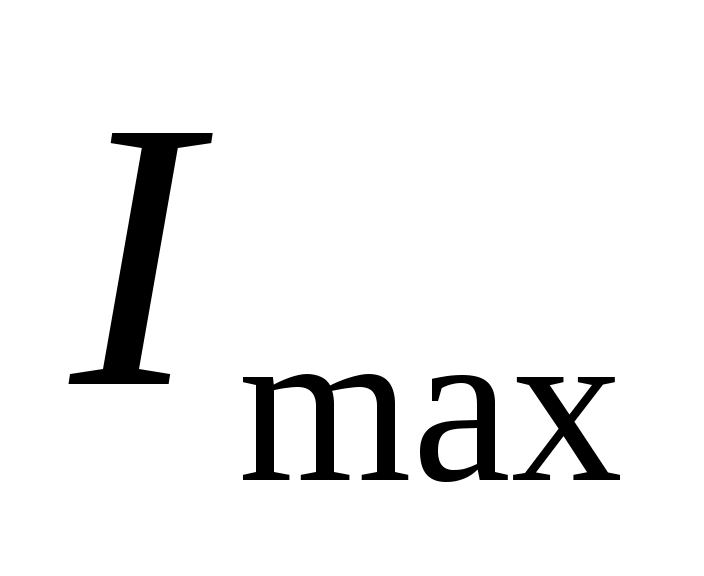 в в 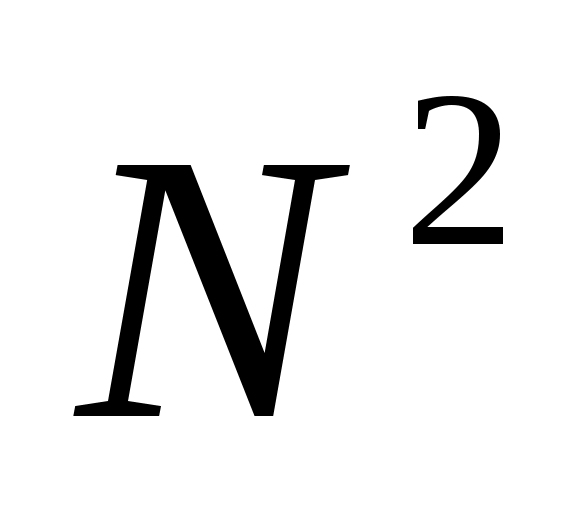 раз больше интенсивности раз больше интенсивности 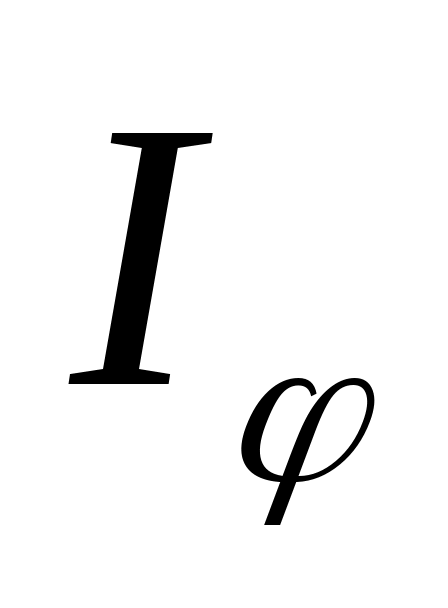 , создаваемой в направлении , создаваемой в направлении 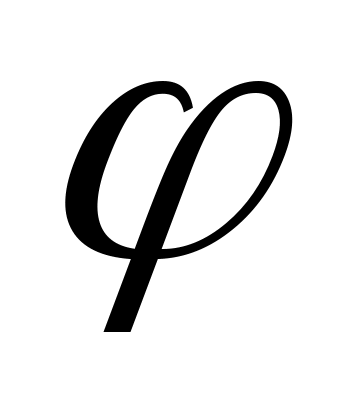 одной щелью. одной щелью. 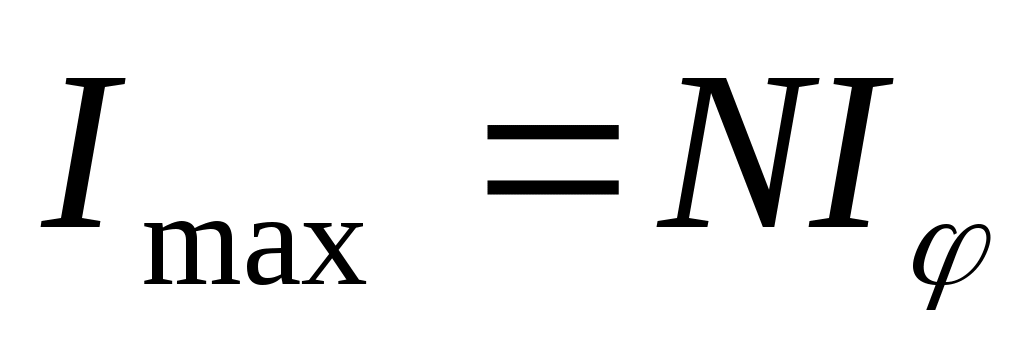 Из условия (19.1) следует, что при Из условия (19.1) следует, что при 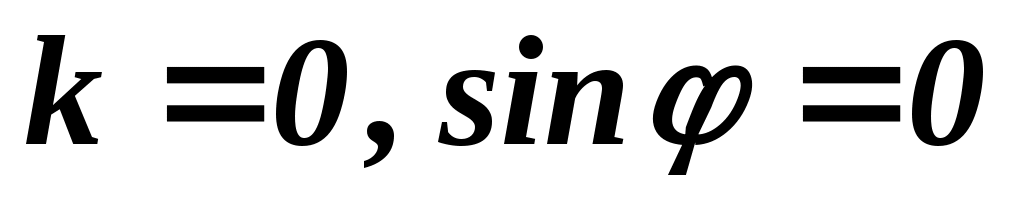 . На экране получается дифракционный максимум, называемый нулевым. При . На экране получается дифракционный максимум, называемый нулевым. При 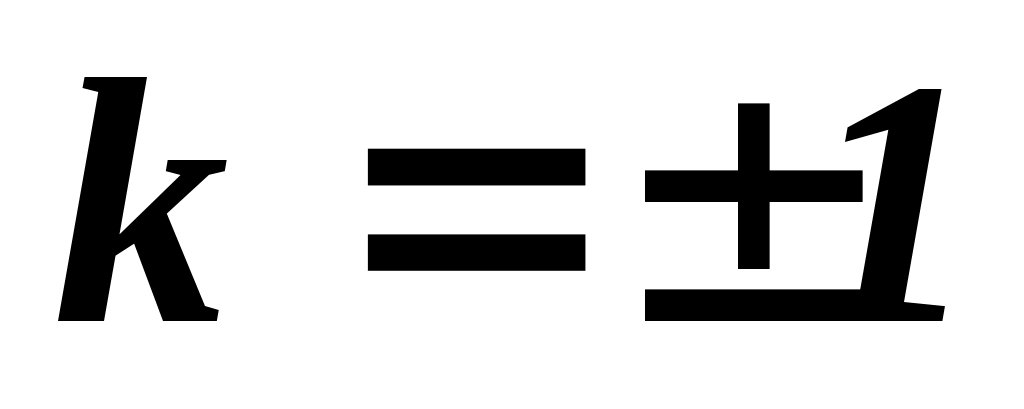 по обе стороны нулевого максимума возникают максимумы первого порядка, по обе стороны нулевого максимума возникают максимумы первого порядка, 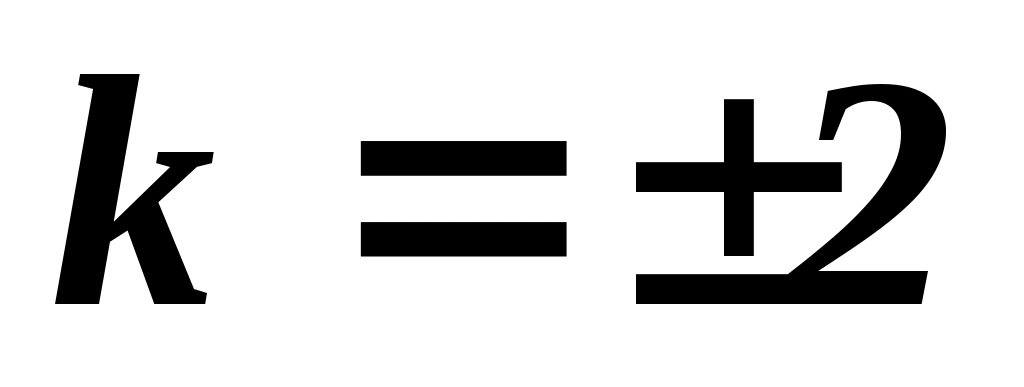 – второго порядка и так далее. При освещении дифракционной решетки белым светом на экране вместо светлых полос будут видны спектры, разделенные темными промежутками. Каждый спектр обращен к нулевому максимуму фиолетовым краем (см. рис. 19.1). Интенсивность максимумов постепенно убывает. Число дифракционных спектров ограничивается условием: – второго порядка и так далее. При освещении дифракционной решетки белым светом на экране вместо светлых полос будут видны спектры, разделенные темными промежутками. Каждый спектр обращен к нулевому максимуму фиолетовым краем (см. рис. 19.1). Интенсивность максимумов постепенно убывает. Число дифракционных спектров ограничивается условием:
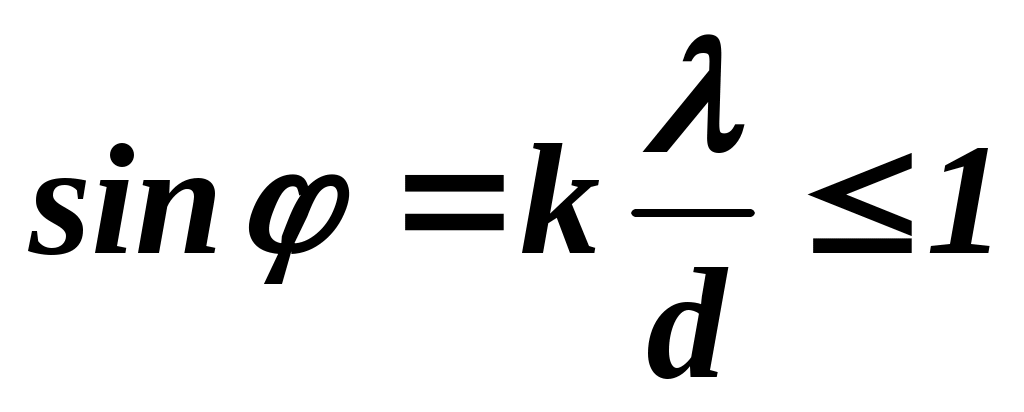 . .
Чем больше период решетки (d), тем большее число спектров можно наблюдать, но тем менее яркими и более узкими становятся отдельные спектральные линии.
|
 Скачать 3.25 Mb.
Скачать 3.25 Mb.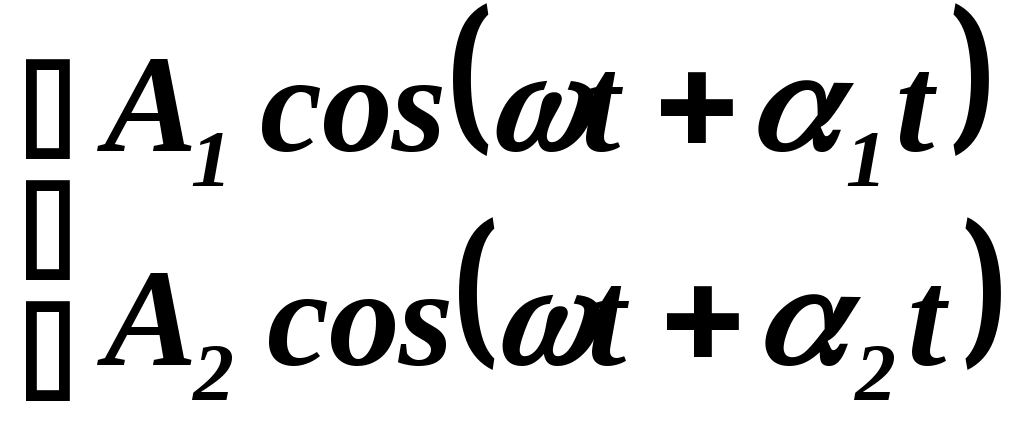 ; б)
; б) 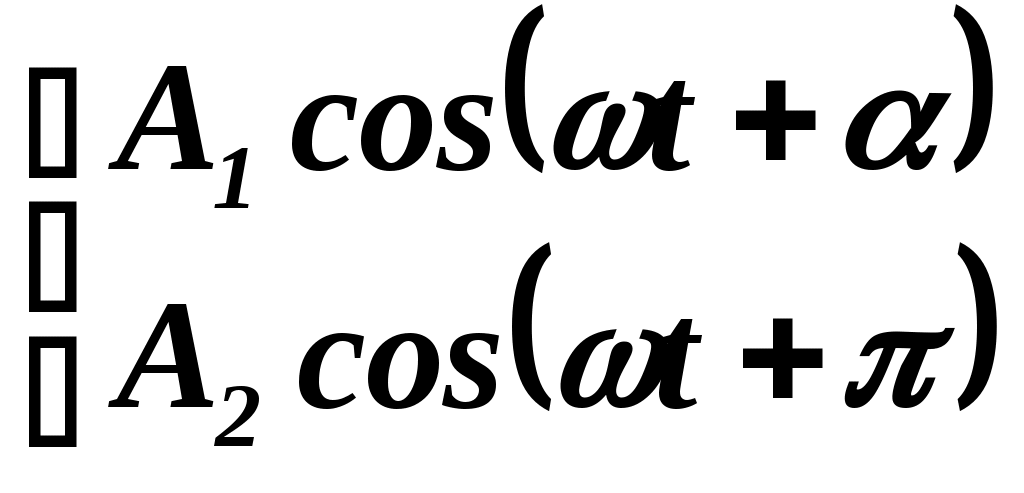 ; в)
; в)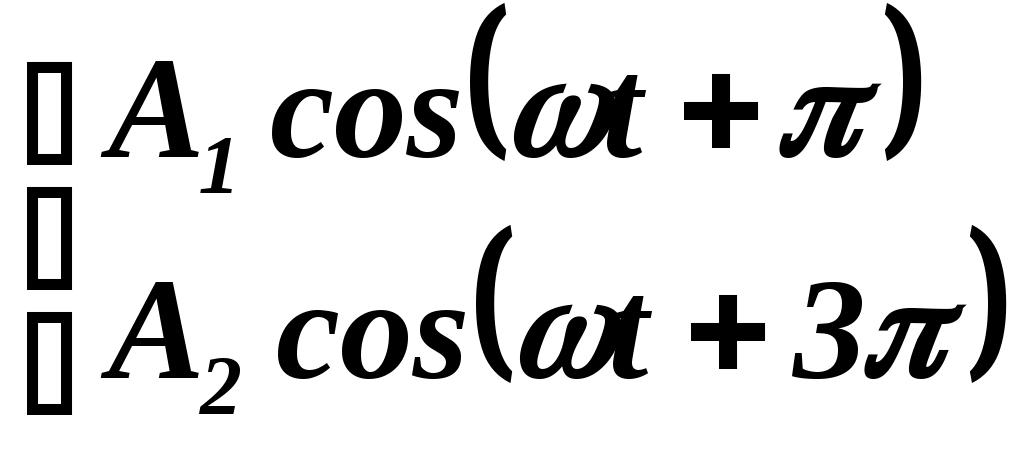 .
.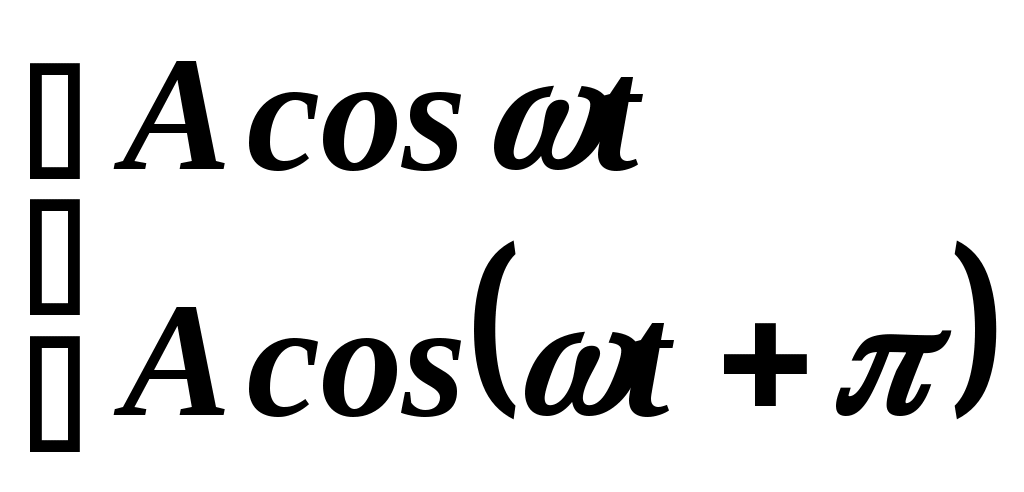 ?
?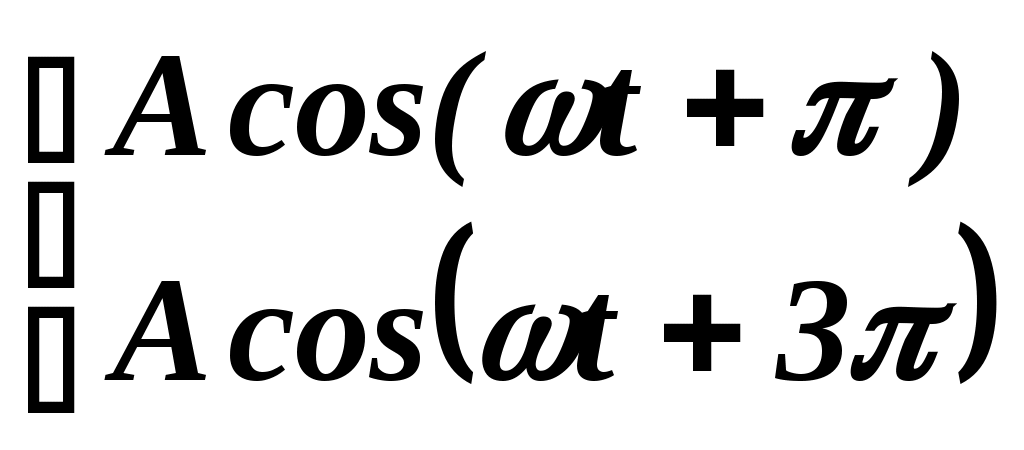 ?
?
 основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны.
основе расчетов дифракции лежит принцип Гюйгенса-Френеля: каждая точка волновой поверхности световых волн является источником когерентных вторичных волн. Огибающая поверхность вторичных волн является новым положением волновой поверхности распространяющейся световой волны. 