Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Арифметические свойства производной Tính chất số học của đạo hàm Пусть f = f(x) и g = g(x) – функции, имеющие конечные производные в точке x0, тогда справедливы равенства: Gọi f = f (x) và g = g (x) là các hàm có đạo hàm hữu hạn tại điểm x0, thì các giá trị bằng nhau sau đây là: 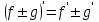 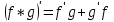 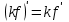 где k – константа trong đó k là hằng số где k – константа trong đó k là hằng số 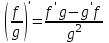 ---------------------------------------------------------------------------------------------------------------------------- 1. 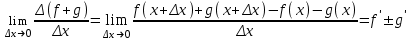 2. 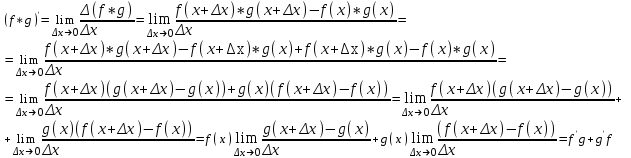 Заметим, что функция f , как имеющая производную, непрерывна, и потому при Lưu ý rằng hàm f, khi có đạo hàm, là liên tục, và do đó, khi 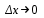 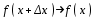 3. 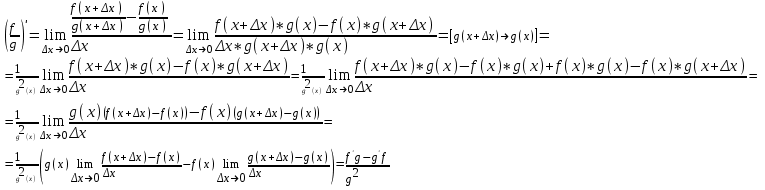 Производная сложной функции. Дифференциал сложной функции. Инвариантность формы первого дифференциала. Đạo hàm của một hàm phức. Vi phân của một hàm hợp chất. Bất biến có dạng của vi phân đầu tiên. Теорема: Пусть функция Để chức năng 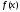 такая, что như vậy mà такая, что như vậy mà 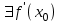 , и функция và chức năng , и функция và chức năng 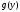 такая, что такая, что 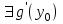 , , 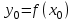 . Тогда сложная функция . Тогда сложная функция 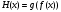 и и 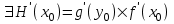 . .Доказательство: 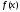 дифференцируема в точке có thể phân biệt ở một điểm дифференцируема в точке có thể phân biệt ở một điểm 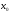 , тогда: , тогда: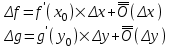 Рассмотрим ∆H: Xét ∆H: 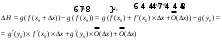 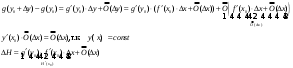 Инвариантность(неизменность от некоторых условий)/Неинвариантность(чаще всего для дифференциалов высшего порядка). Bất biến (bất biến trong những điều kiện nhất định) / Không bất biến (thường xảy ra đối với vi phân bậc cao). 1) y(x), x – независимая переменная 1) y (x), x là một biến độc lập, , 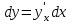 , пусть x = x(t) , x – зависимая переменная biến phụ thuộc ,тогда , пусть x = x(t) , x – зависимая переменная biến phụ thuộc ,тогда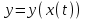 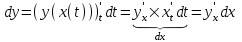 2) y(x), x – независимая переменная biến độc lập , 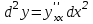 , пусть , пусть 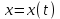 , x – зависимая переменная,тогда , x – зависимая переменная,тогда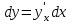 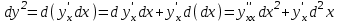 , здесь , здесь 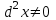 , , 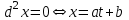 . .Производная обратной функции. Нахождение производных элементарных функций. Đạo hàm của hàm ngược. Tìm đạo hàm của các hàm sơ cấp. Теорема: Пусть на интервале (a,b) задана непрерывная строго монотонная, функция 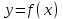 . Пусть образ (a,b) есть интервал (A,B). тогда обратная к Cho trên khoảng (a, b) một hàm số đơn điệu liên tục. Gọi ảnh (a, b) là khoảng (A, B). sau đó đảo ngược thành . Пусть образ (a,b) есть интервал (A,B). тогда обратная к Cho trên khoảng (a, b) một hàm số đơn điệu liên tục. Gọi ảnh (a, b) là khoảng (A, B). sau đó đảo ngược thành 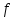 функция функция 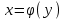 есть однозначная непрерывная и строго монотонная на (A,B) функция. là một hàm đơn điệu liên tục và có giá trị duy nhất trên (A, B). есть однозначная непрерывная и строго монотонная на (A,B) функция. là một hàm đơn điệu liên tục và có giá trị duy nhất trên (A, B). Доказательство: Зафиксируем Hãy sửa chữa 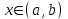 и дадим ему приращение và cung cấp cho nó một gia số и дадим ему приращение và cung cấp cho nó một gia số 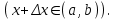 Тогда Тогда 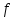 получит соответствующее приращение sẽ nhận được mức tăng tương ứng получит соответствующее приращение sẽ nhận được mức tăng tương ứng 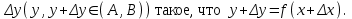 Наоборот Ngược lại , 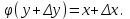 Вследствие непрерывности прямой и обратной функций для указанных Do tính liên tục của các hàm trực tiếp và nghịch đảo đối với 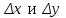 имеет место утверждение có một khẳng định: из имеет место утверждение có một khẳng định: из 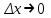 следует следует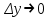 , и обратно. trở lại. , и обратно. trở lại. Пусть теперь функция 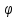 в точке у имеет неравную нулю производную tại điểm y có đạo hàm khác 0 в точке у имеет неравную нулю производную tại điểm y có đạo hàm khác 0 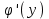 . Покажем, что в таком случае функция Hãy để chúng tôi chỉ ra rằng trong trường hợp này, hàm . Покажем, что в таком случае функция Hãy để chúng tôi chỉ ra rằng trong trường hợp này, hàm 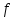 также имеет в соответствующей точке х производную. В самом деле, cũng có đạo hàm tại điểm x tương ứng. Thật, также имеет в соответствующей точке х производную. В самом деле, cũng có đạo hàm tại điểm x tương ứng. Thật, 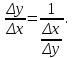 Так как из того Kể từ cái gì , что 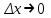 следует, что следует, что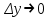 , то , то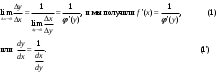 Этим доказано, что если 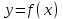 есть строго монотонная непрерывная функция là một hàm liên tục đơn điệu nghiêm ngặt и есть строго монотонная непрерывная функция là một hàm liên tục đơn điệu nghiêm ngặt и 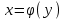 обратная к ней функция, имеющая в точке у производную обратная к ней функция, имеющая в точке у производную 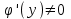 , то функция , то функция 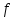 имеет в соответствующей точке х производную, определяемую формулой (1). có đạo hàm tại điểm x tương ứng, được xác định bởi công thức (1). имеет в соответствующей точке х производную, определяемую формулой (1). có đạo hàm tại điểm x tương ứng, được xác định bởi công thức (1). Может случиться Có thể xảy ra , что в точке 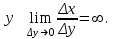 В этом случае, очевидно Trong trường hợp này, rõ ràng , функция В этом случае, очевидно Trong trường hợp này, rõ ràng , функция 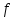 имеет в соответствующей точке х производную có đạo hàm tại điểm x tương ứng имеет в соответствующей точке х производную có đạo hàm tại điểm x tương ứng 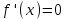 . .Если же 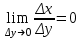 , то для строго возрастающей функции при этом sau đó cho một chức năng tăng nghiêm ngặt, trong trường hợp này , то для строго возрастающей функции при этом sau đó cho một chức năng tăng nghiêm ngặt, trong trường hợp này 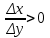 , а для строго убывающей và để giảm một cách nghiêm ngặt , а для строго убывающей và để giảm một cách nghiêm ngặt 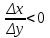 . В первом случае Trong trường hợp đầu tiên . В первом случае Trong trường hợp đầu tiên 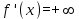 , а во втором , а во втором 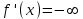 . .Пример 1. 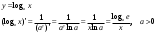 Если логарифм натуральный, то Nếu lôgarit là tự nhiên, thì 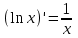 . .Функция ln x как действительная функция определена только для положительных значений х. Hàm ln x là một hàm thực chỉ được xác định cho các giá trị dương của x. Пример 2. 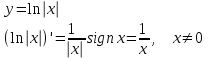 где 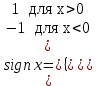 Пример 3. 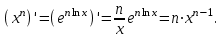 Пример 4. Функция 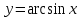 строго возрастает на отрезке [-1,1] и отображает этот отрезок на tăng nghiêm ngặt trên phân đoạn [-1,1] và ánh xạ phân đoạn này tới строго возрастает на отрезке [-1,1] и отображает этот отрезок на tăng nghiêm ngặt trên phân đoạn [-1,1] và ánh xạ phân đoạn này tới 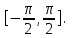 Обратная к ней функция Đảo ngược Обратная к ней функция Đảo ngược 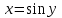 имеет производную имеет производную 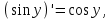 положительную на интервале có một đạo hàm положительную на интервале có một đạo hàm 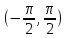 . Поэтому . Поэтому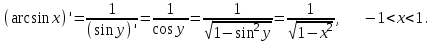 Пример 5. 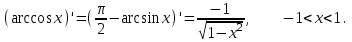 Пример 6. 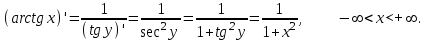 Производные элементарных функций. Đạo hàm của các hàm sơ cấp. 1. 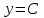 ; ; 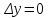 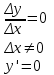 2. 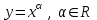 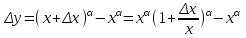 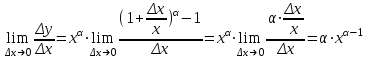 3. 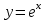 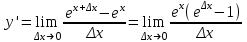 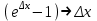 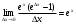 4. 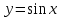 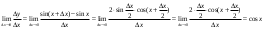 (т.к. функция непрерывна) (т.к. функция непрерывна)Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке , но она может быть разрывной в любой другой точке, кроме этой. Lưu ý: nếu một hàm có đạo hàm hữu hạn tại một điểm thì nó liên tục tại điểm đó, nhưng nó có thể không liên tục tại bất kỳ điểm nào khác ngoài điểm này. Пример: 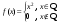 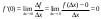 , т.к. , т.к.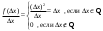 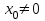 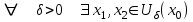 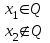 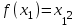 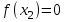 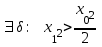 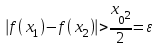 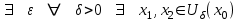 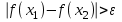 - не выполняется критерий Коши и в каждой точке - не выполняется критерий Коши и в каждой точке 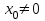 функция разрывна. tiêu chí Cauchy không được thỏa mãn và hàm không liên tục tại mỗi điểm. функция разрывна. tiêu chí Cauchy không được thỏa mãn và hàm không liên tục tại mỗi điểm. Производные высших порядков. Производные высших порядков для основных элементарных функций. Phái sinh của đơn đặt hàng cao hơn. Đạo hàm bậc cao cho các hàm sơ cấp cơ bản. Пусть задана функция y=f(x) дифференцируема в точке Xo и в некоторой U(Xo)., то есть существует ее производная в этой точке f ’ (Xo), определеная в U(Xo) и если дифференцируема в точке Xo, то (f’(Xo))’=f’’(Xo). Cho hàm số y = f (x) đã cho và khả vi tại điểm Xo và tại điểm U (Xo) nào đó. (F '(Xo))' = f '' (Xo) Вообще Nói chung 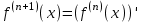 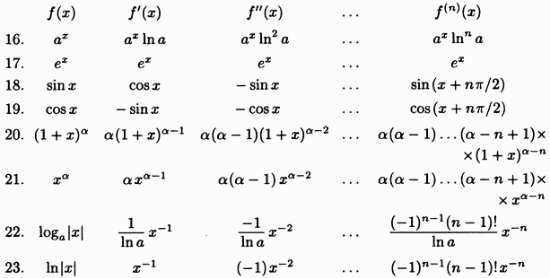 Формула Лейбница. Công thức Leibniz. Пусть функции U и V n раз диффер енцируемы, т.е. существуют Để các hàm U và V phân biệt được n lần, tức là tồn tại 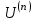 и и 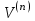 . Значит (U*V) – тоже n раз дифференцируема, при этом Do đó (U * V) cũng có thể phân biệt được n lần, trong khi . Значит (U*V) – тоже n раз дифференцируема, при этом Do đó (U * V) cũng có thể phân biệt được n lần, trong khi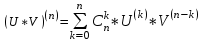 Доказательство: Метод математической индукции: Phương pháp quy nạp toán học: Пусть при n=m – верно, т.е. 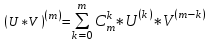 (*) (*)Надо доказать, что 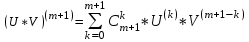 Доказательство: 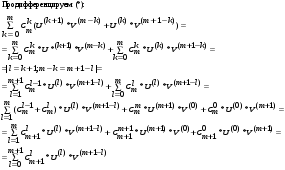 Теорема доказана. Định lý đã được chứng minh. Вычисление производных и дифференциалов неявно заданных функций. Tính đạo hàm và vi phân của các hàm đã cho ngầm định. Пусть функция задана уравнением F(x,y)=0. Для вычисления производной функции y=f(x) нужно продифференцировать обе части уравнения, считая y=y(x)- функцией от x, а затем из полученного уравнения найти производную. Cho hàm số đã cho bởi phương trình F (x, y) = 0. Để tính đạo hàm của hàm y = f (x), bạn cần phân biệt cả hai phần của phương trình, coi y = y (x) là một hàm của x, sau đó tìm đạo hàm từ phương trình thu được. Вычисление производных функций, заданных параметрически. Tính đạo hàm của hàm số đã cho theo tham số. Дифференциалы высших порядков. Неинвариантность формы дифференциалов высших порядков. Vi phân bậc cao hơn. Tính bất biến của dạng vi phân bậc cao hơn. f(x) дифференцируема, Если х-не зависимая переменная, то dx-не зависит от точки f (x) là phân biệt được, Nếu x độc lập với biến, thì dx không phụ thuộc vào điểm 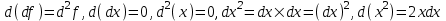 тогда 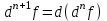 . Далее, пусть f – nраз дифференцируема Hơn nữa, giả sử có thể phân biệt n lần, , . Далее, пусть f – nраз дифференцируема Hơn nữa, giả sử có thể phân biệt n lần, , 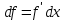 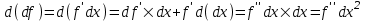 __________________________ 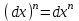 . . Докажем Hãy chứng minh , что (d^(n)f)= 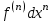 при помощи мат với sự giúp đỡ của một tấm thảm. Индукции hướng dẫn при помощи мат với sự giúp đỡ của một tấm thảm. Индукции hướng dẫn 1) 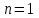 , , 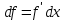 2) Пусть при n = m 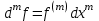 3) 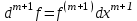 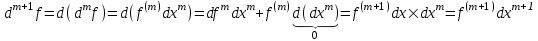 Инвариантность(неизменность от некоторых условий)/Неинвариантность(чаще всего для дифференциалов высшего порядка). Bất biến (bất biến trong những điều kiện nhất định) / Không bất biến (thường xảy ra đối với vi phân bậc cao). 1) y(x), x – независимая переменная, biến độc lập 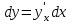 , пусть x = x(t) , x – зависимая переменная, biến phụ thuộc тогда , пусть x = x(t) , x – зависимая переменная, biến phụ thuộc тогда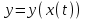 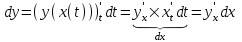 2) y(x), x – независимая переменная, 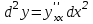 , пусть , пусть 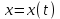 , x – зависимая переменная,тогда , x – зависимая переменная,тогда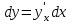 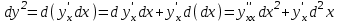 , здесь , здесь 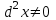 , , 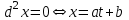 . . |
