Сандық әдістер. Осауленко Роман Николаевич, доцент, кафедра физики твердого тела председатель учебнометодической комиссии института, Физикотехнический институт, кандидат физикоматематических наук, доцент рабочая программа дисциплины
 Скачать 80.91 Kb. Скачать 80.91 Kb.
|
|
Годы обучения по образовательной программе 2020-2025 Петрозаводский государственный университет Физико-технический институт Кафедра информационно-измерительных систем и физической электроники УТВЕРЖДАЮ Проректор по учебной работе ______________ К.Г. Тарасов «____» ________ 2020 г. Рабочая программа дисциплины ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА Направление подготовки бакалавриата 44.03.05 Педагогическое образование (с двумя профилями подготовки) Профили направления подготовки бакалавриата «Образование в предметных областях (Физика и информатика)» Форма обучения очная Петрозаводск 2020 Рабочая программа дисциплины разработана в соответствии с ФГОС ВО, утвержденным приказом Министерства образования и науки Российской Федерации от 22.02.2018 г. № 125 и учебным планом по направлению подготовки бакалавриата 44.03.05 Педагогическое образование (с двумя профилями подготовки). Профили «Образование в предметных областях (Физика и информатика)». Разработчик: Балашов Дмитрий Игоревич, директор, Физико-технический институт, кандидат физико-математических наук; _________________________________ (подпись) Эксперт: Осауленко Роман Николаевич, доцент, кафедра физики твердого тела; председатель учебно-методической комиссии института, Физико-технический институт, кандидат физико-математических наук, доцент Рабочая программа дисциплины рассмотрена и одобрена на заседании кафедры информационно-измерительных систем и физической электроники Протокол № _________ от «______» ___________ 201__ г. Заведующий кафедрой ____________________________ (к. ф.-м. н., доцент Н. Ю. Ершова) (подпись) СОГЛАСОВАНО: Рабочая программа дисциплины рассмотрена и утверждена на заседании учебно-методической комиссии физико-технического института. Протокол № 4 от «28» июня 2018 г. Директор института _________________________________ (к. ф.-м. н., Д. И. Балашов) (подпись) Начальник методического отдела учебно-методического управления ПетрГУ _________________________ И.В. Маханькова 1. Перечень планируемых результатов обучения по дисциплине, соотнесенных с планируемыми результатами освоения основной профессиональной образовательной программы (ОПОП) бакалавриата Компетенции обучающегося, формируемые в результате освоения дисциплины:
В ходе изучения дисциплины обучающийся должен: Знать: - основные численные методы для решения инженерных и физических задач современными средствами вычислительной техники, в том числе и в области образования; - основы алгоритмизации и особенностях программирования на одном из языков высокого уровня (Паскаль, Фортран, Си или др.); - теоретические основы изучаемых численных методов; - достоинства и недостатки различных численных методов; - условия применимости различных методов вычислительной математики для решения конкретных математических, физических и технических задач. Уметь: - составлять алгоритмы различного уровня сложности или использовать готовые алгоритмы на практике для решения поставленной задачи; - определять области применения численных методов для решения конкретных математических, технических и физических задач; - на практике реализовывать различные методы численного решения задач. Владеть: - основными навыками составления элементарных программ на языке высокого уровня; - методикой использования стандартных прикладных программ для решения инженерных и физических задач и задач в области образования; - методикой выбора оптимальных процедур численного решения, сравнения результатов решений задачи, полученных различными методами; - навыками пользования методиками проверки правильности и точности получаемых численных решений, а также методиками проверки сходимости и скорости получения решения для обоснования корректности применения конкретных алгоритмов численного решения; - методикой составления алгоритмов и программ для реализации численных методов на одном из языков программирования высокого уровня. 2. Место дисциплины в структуре ОПОП бакалавриатаи язык преподавания Дисциплина «Вычислительная математика» входит в часть, формируемую участниками образовательных отношений учебного плана основной образовательной программы бакалавриата по данному направлению подготовки и является обязательной для изучения дисциплиной. Согласно учебному плану дисциплина проводится в 3 семестре. Изучение дисциплины опирается на знания, умения и навыки, приобретенные при освоении образовательной программы предыдущего уровня, а также при изучении дисциплин: Информатика, Математический анализ, Алгебра и геометрия. Язык преподавания – русский. 3. Виды учебной работы и тематическое содержание дисциплины Общая трудоемкость дисциплины составляет 3 зачетных единиц или 108 академических часов. 3.1. Виды учебной работы
3.2. Краткое содержание дисциплины по разделам и видам учебной работы
3.3. Содержание аудиторных занятий Содержание лекционных занятий
Содержание лабораторных занятий
3.4. Организация самостоятельной работы обучающегося
4. Образовательные технологии по дисциплине При преподавании дисциплины "Вычислительная математика" может быть реализована технологии балльно-рейтинговой оценки знаний обучающихся. Специфическим средством, применяемым в ходе преподавания рассматриваемой дисциплины, является система проведения тестирования студентов IQ. Данная система была разработана коллективом преподавателей кафедры информационно-измерительных систем и физической электроники. Система позволяет проводить индивидуальное тестирование и оценку студентов по различным дисциплинам или различным модулям дисциплины. Система удовлетворяет большинству требований, предъявляемым к системам тестирования такого уровня. Вопросы тестов по дисциплине «Численные методы» были разработаны и включены в систему непосредственно преподавателем, ведущим занятия. Также к несомненным достоинствам системы IQ можно отнести тот факт, что система работает через web-интерфейс. Это значит, что она может быть доступна для работы с любого компьютера, подключенного к локальной сети университета, а также с большинства компьютеров, имеющих доступ в сеть Интернет. 5. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации обучающихся по дисциплине 5.1. Текущий контроль осуществляется преподавателем дисциплины при проведении занятий в форме: лабораторная работа, тест, экзамен. Оценочные средства для текущего контроля. Оценочное средство: тест. Пример: Перечислите достоинства метода дихотомии. Укажите недостаток метода дихотомии. Укажите достоинство метода касательных. Перечислите недостатки метода касательных. В каких методах необходимо задавать интервал изоляции корня [a, b]? В каких методах необходимо задавать начальное приближение корня х0? Продолжите теорему о существовании корней уравнения f(x)=0 на интервале [a, b]: Если на концах интервала [a, b] функция f(x) имеет разные знаки, то на интервале [a, b] уравнение f(x)=0 ... Какие уравнения называют трансцендентными? Какие данные необходимо задать для реализации метода дихотомии? Какие данные необходимо задать для реализации метода хорд? Какие данные необходимо задать для реализации метода касательных? Какие данные необходимо задать для реализации метода секущих? Каков графический смысл производной функции? Перечислите устойчивые методы решения нелинейных уравнений. Используя неустойчивый метод для решения нелинейных уравнений, будет ли гарантировано нахождение корня? Какой метод используют для нахождения интервала изоляции корня? Метод секущих является модификацией какого метода? Критерии оценивания: тест считается пройденным (оценка «зачтено»), если обучающийся набрал не менее 60% правильных ответов на вопросы. Всего выполняется 6 тестов на знание теории каждого из 6 разделов дисциплины. Оценочное средство: лабораторная работа. Пример задания: Задача 1 Вариант 20 (Решение алгебраического уравнения с одним неизвестным) Найти корень уравнения 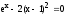 с точностью с точностью 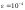 в интервале изоляции корня [0;1] методом хорд и методом касательных. в интервале изоляции корня [0;1] методом хорд и методом касательных.-------------------------------------------------------------------------------- Задача 2 Вариант 20 (Решение систем линейных алгебраических уравнений) Решить систему уравнений Ax=b методом Гаусса и методом Зейделя, где 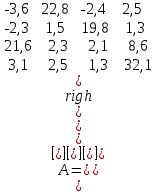 ; ; 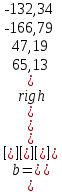 ; ; 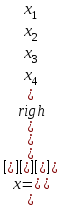 , с точностью , с точностью 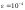 . .В электронных таблицах Excel решить данную систему методом Крамера. -------------------------------------------------------------------------------- Задача 3 Вариант 20 (Решение систем нелинейных алгебраических уравнений) Решить систему уравнений 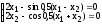 Точность =10-5.Начальное приближение х0=(0; 0.5). Точность =10-5.Начальное приближение х0=(0; 0.5).-------------------------------------------------------------------------------- Задача 4 Вариант 20 (Численное интегрирование) Методами средних прямоугольников, трапеций и Симпсона вычислить интеграл функции y(x)= 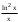 в интервале [1;5] с разбиением на 50 частей. Вычислить абсолютную погрешность формул численного интегрирования, зная первообразную данной функции в интервале [1;5] с разбиением на 50 частей. Вычислить абсолютную погрешность формул численного интегрирования, зная первообразную данной функции 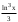 . Сравнить разные способы вычисления. . Сравнить разные способы вычисления.-------------------------------------------------------------------------------- Задача 5 Вариант 20 (Интерполяция функций) Интерполировать заданную таблично функцию полиномами 1-го порядка (локальная линейная интерполяция) и полиномом n-го порядка (глобальная интерполяция). Вычислить значение функции в точке x: xi= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 yi=0.55, 0.30, 0.13, 0.07, 0.04, 0.01, 0.00, 0.71, 0.50, 0.32, 0.22, 0.16, 0.10, 0.05, 0.68, 0.51, 0.32, 0.16, 0.11, 0.08 в точке х=6.42. (Аппроксимация функций) Аппроксимировать табличную функцию из предыдущей задачи полиномом 1 и 2 степени. Используя полученную аппроксимацию, вычислить значение функции в точке, указанной в предыдущей задаче. На одной координатной плоскости построить график исходной табличной функции и графики аппроксимирующих полиномов. -------------------------------------------------------------------------------- Задача 6 Вариант 20 (Решение задачи Коши О.Д.У.) Численно решить дифференциальное уравнение 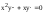 при начальных условиях y(1)=5, при начальных условиях y(1)=5, 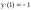 в интервале интегрирования [1;1.5] с шагом h=0.05. Определить близость полученного заданным методом решения к точному значению с помощью линейной оценки: в интервале интегрирования [1;1.5] с шагом h=0.05. Определить близость полученного заданным методом решения к точному значению с помощью линейной оценки: 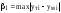 , где , где 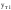 - точное решение, - точное решение, 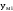 - полученное приближенное решение. Точное решение: - полученное приближенное решение. Точное решение: 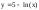 . На одной координатной плоскости построить график зависимости y=y(x) решения уравнения численным методом (точки) и точного решения (линия). Задачу решить с использованием двух методов: Эйлера и Рунге–Кутта 4 порядка. . На одной координатной плоскости построить график зависимости y=y(x) решения уравнения численным методом (точки) и точного решения (линия). Задачу решить с использованием двух методов: Эйлера и Рунге–Кутта 4 порядка.Критерии оценивания: Лабораторная работа считается выполненной (оценка «Зачтено», если: Составлена программа для решения соответствующей задачи. Получен достоверный результат. Проведена проверка полученного результата. Представлен письменный отчет о выполнении лабораторной работы. Каждое индивидуальное задание для лабораторных работ состоит из 6 задач. 5.2. Промежуточная аттестация проводится в виде: экзамен. Вопросы к экзамену Решение нелинейных уравнений. Теорема о существовании корня. Метод половинного деления: характеристика, графическая интерпретация, алгоритм, достоинства и недостатки. Решение нелинейных уравнений. Теорема о существовании корня. Метод хорд: характеристика, графическая интерпретация, алгоритм, достоинства и недостатки. Решение нелинейных уравнений. Метод касательных: характеристика, графическая интерпретация, алгоритм, достоинства и недостатки. Сходимость и расходимость метода. Характеристика СЛАУ. Классификация СЛАУ в зависимости от количества решений. Условие единственности решения СЛАУ. Характеристика метода Гаусса. Решение СЛАУ методом Гаусса: алгоритмы прямого и обратного хода. Характеристика СЛАУ. Классификация СЛАУ в зависимости от количества решений. Условие единственности решения СЛАУ. Характеристика метода Зейделя. Решение СЛАУ методом Зейделя: алгоритм. Сходимость и расходимость метода. Условие сходимости метода Зейделя. Характеристика систем нелинейных уравнений. Решение систем нелинейных уравнений методом Зейделя: алгоритм, условие применимости, примеры. Характеристика систем нелинейных уравнений. Решение систем нелинейных уравнений методом Ньютона: алгоритм, условие применимости. Основы методов численного интегрирования. Методы прямоугольников (левых, правых, средних): расчетные формулы и алгоритмы. Основы методов численного интегрирования. Метод трапеций: расчетная формула и алгоритм. Погрешность численного интегрирования: сравнительный анализ методов. Основы методов численного интегрирования. Метод Симпсона: расчетная формула, особенности. Интерполяция и аппроксимация функций: общие положения, постановка задачи. Глобальная и локальная интерполяция. Экстраполяция. Метод линейной интерполяции: алгоритм, особенности. Интерполяция и аппроксимация функций: общие положения, постановка задачи. Глобальная и локальная интерполяция. Глобальная интерполяция методом канонических полиномов: алгоритм, особенности. Интерполяция и аппроксимация функций: общие положения, постановка задачи. Глобальная и локальная интерполяция. Глобальная интерполяция методом полинома Лагранжа: алгоритм, особенности. Интерполяция и аппроксимация функций: общие положения, постановка задачи. Метод наименьших квадратов: основные положения, графическая интерпретация и основная расчетная формула. Аппроксимация линейной функцией. Интерполяция и аппроксимация функций: общие положения, постановка задачи. Метод наименьших квадратов: основные положения, графическая интерпретация и основная расчетная формула. Аппроксимация квадратичной функцией. Обыкновенные дифференциальные уравнения: общий вид, аналитические и численные решения ОДУ. Метод Эйлера: характеристика, графическая интерпретация и расчетная формула. Обыкновенные дифференциальные уравнения: общий вид, аналитические и численные решения ОДУ. Метод Эйлера-Коши: характеристика, графическая интерпретация и расчетная формула. Обыкновенные дифференциальные уравнения: общий вид, аналитические и численные решения ОДУ. Метод Рунге-Кутты 4 порядка и метод Адамса: расчетные формулы и сравнительная характеристика методов. Решение систем дифференциальных уравнений. Методы Эйлера и Эйлера-Коши. Расчетные формулы. Решение дифференциальных уравнений старших порядков. Методы Эйлера и Эйлера-Коши. Расчетные формулы. Подробно средства оценивания для проведения промежуточной аттестации обучающихся приведены в Фонде оценочных средств по данной дисциплине. 6. Методические рекомендации обучающимся по дисциплине, в том числе для самостоятельной работы При подготовке к занятиям в текущем режиме обучающимся следует: 1. По каждой теме получить индивидуальное задание у преподавателя. 2. Изучив теорию используемых численных методов, на языке программирования высокого уровня, например Free Pascal, составить программу, реализующую алгоритм данного численного метода (методов). 3. Получить результаты расчетов и проанализировать их на адекватность и точность. 4. Оформить отчет в письменной форме по следующим пунктам: - Текст задания; - Краткая теория используемых методов; - Блок-схемы используемых методов; - Тексты программ; - Полученные результаты; - Проверка полученных результатов; - Выводы по работе. 5. На сайте iq.karelia.ru пройти тестирование на знание теории соответствующего раздела дисциплины. Средства авторизации в тестовой системе выдается преподавателем. Тест считается успешно пройденным, если получена оценка не ниже 3 баллов по пятибалльной шкале. 7. Методические рекомендации преподавателям по дисциплине Преподавателям, проводящим лабораторные занятия со студентами, следует обращать внимание на грамотность написания программ студентами, а также на интерпретацию полученных результатов, оценку их адекватности и точности. По каждой программе преподавателем проводится собеседование со студентом на предмет понимания реализуемого алгоритма, а также на грамотное использование соответствующих операторов, функций и конструкций языка программирования. 8. Учебно-методическое и информационное обеспечение дисциплины Библиографический список документов 8.1. Основная литература: Балабко, Л.В. Численные методы : учебное пособие / Л.В. Балабко, А.В. Томилова ; Министерство образования и науки Российской Федерации, Северный (Арктический) федеральный университет имени М.В. Ломоносова. - Архангельск : САФУ, 2014. - 163 с. : схем., табл., ил. - ISBN 978-5-261-00962-7 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=436331. Пименов, В.Г. Численные методы : учебное пособие : в 2 ч. / В.Г. Пименов, А.Б. Ложников ; Министерство образования и науки Российской Федерации, Уральский федеральный университет им. первого Президента России Б. Н. Ельцина, Ю.А. Меленцова. - Екатеринбург : Издательство Уральского университета, 2014. - Ч. 2. - 107 с. : ил., табл., схем. - Библиогр. в кн. - ISBN 978-5-7996-1342-6 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=275819. Соболева, О.Н. Введение в численные методы : учебное пособие / О.Н. Соболева. - Новосибирск : НГТУ, 2011. - 64 с. - ISBN 978-5-7782-1776-8 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=229144. 8.2. Дополнительная литература: Гавришина, О.Н. Практикум по численным методам : учебное пособие / О.Н. Гавришина, Ю.Н. Захаров. - Кемерово : Кемеровский государственный университет, 2011. - 74 с. - ISBN 978-5-8353-1180-4 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=232353. Турчак, Л.И. Основы численных методов : учебное пособие / Л.И. Турчак, П.В. Плотников. - 2-е изд., перераб. и доп. - Москва : Физматлит, 2002. - 304 с. - ISBN 5-9221-0153-6 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=69329. 8.3. Программное обеспечение и Интернет-ресурсы: ОС Microsoft Windows, ОС Linux; пакет офисных приложений Microsoft Office; интегрированная среда разработки и компилятор языка Паскаль (Free Pascal). 8.4. Информационное обеспечение дисциплины в системе электронного (дистанционного) обучения нет 9. Материально-техническое обеспечение дисциплины Материально-техническая база ПетрГУ обеспечивает проведение всех видов дисциплинарной и междисциплинарной подготовки, практической и научно-исследовательской работы обучающихся, предусмотренных учебным планом и соответствует действующим санитарным и противопожарным правилам и нормам. Минимально-необходимый перечень для информационно-технического и материально-технического обеспечения дисциплины: аудитория для проведения лекционных и практических занятий, оснащенная рабочими местами для обучающихся и преподавателя, доской, мультимедийным оборудованием; библиотека с читальным залом и залом для самостоятельной работы обучающегося, оснащенное компьютером с выходом в Интернет, книжный фонд которой составляет специализированная научная, учебная и методическая литература, журналы (в печатном или электронном виде); компьютерные классы: 105, 110 или 346 учебно-лабораторного корпуса №6 Дата «_____» _________ 2020 г. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
