термодинамика реферат. Основные понятия и исходные положения термодинамики

• Название: Основные понятия и исходные положения термодинамики
• Анкор: термодинамика реферат
• Дата: 07.06.2021
• Размер: 141.71 Kb.
• Имя файла: bestreferat-59647.docx
• Тип: Реферат; #214807
• страница: 3 из 4

ГЛАВА 3

АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ

САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ СИСТЕМ.
3.1. ЯЧЕЙКИ БЕНАРА .
Для того , чтобы экспериментально изучить структуры , достаточно иметь сковороду , немного масла и какой ни будь мелкий порошок , чтобы было заметно движение жидкости . Нальем в сковороду масло с размешанным в нем порошком и будем подогревать ее снизу (рис. 3.1)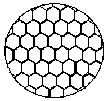



Рис. 3.1. Конвективные ячейки Бенара.

Если дно сковороды плоское и нагреваем мы ее равномерно , то можно считать , что у дна и на поверхности поддерживаются постоянные температуры , снизу - Т₁ , сверху - Т₂ . Пока разность температуры Т = Т₁ - Т₂ невелика , частички порошка неподвижны , а следовательно , неподвижна и жидкость .

Будем плавно увеличивать температуру Т₁ . С ростом разности температур до значения Т_c наблюдается все та же картина , но когда Т  Т_c , вся среда разбивается на правильные шестигранные ячейки (см. Рис. 3.1) в центре каждой из которых жидкость движется вверх , по кроям вниз . Если взять другую сковороду , то можно убедиться , что величина возникающих ячеек практически не зависит от ее формы и размеров . Этот замечательный опыт впервые был проделан Бенаром в начале нашего века , а сами ячейки получили название ячеек Бенара .

Элементарное качественное объяснения причины движения жидкости заключается в следующем . Из-за теплового расширения жидкость расслаивается , и в более нижнем слое плотность жидкости ₁ меньше , чем в верхнем ₂ . Возникает инверсный градиент плотности , направленный противоположно силе тяжести . Если выделить элементарный объем V , который немного смещается вверх в следствии возмущения , то в соседнем слое архимедова сила станет больше силы тяжести , так как ₂  ₁ . В верхней части малый объем , смещаясь вниз , поподает в облость пониженной плотности , и архимедова сила будет меньше силы тяжести F_A < F_T , возникает нисходящее движение жидкости . Направление движения нисходящего и восходящего потоков в данной ячейке случайно , движение же потоков в соседних ячейках , после выбора направлений в данной ячейке детерминировано . Полный поток энтропии через границы системы отрицателен , то есть система отдает энтропию , причем в стационарном состоянии отдает столько , сколько энтропии производится внутри системы (за счет потерь на трение).

dS_e q q T₁ - T₂

=  -  = q   < 0 (3.1)

dt T₂ T₁ T₁  T₂

Образование именно сотовой ячеистой структуры объясняется минимальными затратами энергии в системе на создание именно такой формы пространственной структуры . При этом в центральной части ячейки жидкость движется вверх , а на ее периферии - вниз.

Дальнейшее сверхкритическое нагревание жидкости приводит к разрушению пространственной структуры - возникает хаотический турбулентный режим.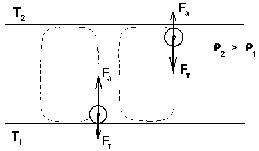



Рис. 3.2. Иллюстрация возникновения тепловой

конвекции в жидкости .

К этому вопросу прикладывается наглядная иллюстрация возникновения тепловой конвекции в жидкости .
ЛАЗЕР , КАК САМООРГАНИЗУЮЩАЯСЯ СИСТЕМА.
Во второй главе этот вопрос мы уже рассматривали . Здесь же , рассмотрим простую модель лазера .

Лазер - это устройство , в котором в процессе стимулированного излучения порождаются фотоны .

Изменение со временем числа фотонов n , или другими словами , скорость порождения фотонов , определяется уравнением вида :
dn / dt = «Прирост» - «Потери» (3.2)
Прирост обусловлен так называемым стимулированном излучением . Он пропорционален числу уже имеющихся фотонов и числу возбужденных атомов N . Таким образом :
Прирост = G N n (3.3)
Здесь G - коэффициент усиления , который может быть получен из микроскопической теории . Член , описывающий потери , обусловлен уходом фотонов через торцы лазера . Единственное допущение , которое мы принимаем , - это то , что скорость ухода пропорциональна числу имеющихся фотонов . Следовательно ,
Потери = 2n (3.4)
2 = 1/ t₀ , где t₀ - время жизни фотона в лазере .

Теперь следует учесть одно важное обстоятельство , которое делает (2.1) нелинейным уравнением вида :

(3.5)

Число возбужденных атомов уменьшается за счет испускания фотонов . Это уменьшение N пропорционально числу имеющихся в лазере фотонов , поскольку эти фотоны постоянно заставляют атомы возвращаться в основное состояние .

N = n (3.6)

Таким образом , число возбужденных атомов равно

N = N₀ - N (3.7)

где N₀ - число возбужденных атомов , поддерживаемое внешней

накачкой , в отсутствии лазерной генерации.

Подставляя (3.3) - (3.7) в (3.2) , получаем основное уравнение нашей упрощенной лазерной модели :

(3.8)

где постоянная k дает выражение :

k₁ = G

k = 2 - GN₀  0 (3.9)

Если число возбужденных атомов N₀ (создаваемых накачкой) невелико , то k положительно , в то время как при достаточно больших N₀ k - может стать отрицательным . Изменение знака происходит когда

GN₀ = 2 (3.10)

Это условие есть условие порога лазерной генерации .

Из теории бифуркации следует , что при k > 0 лазерной генерации нет , в то время как при k < 0 лазер испускает фотоны.

Ниже или выше порога лазер работает в совершено разных режимах .

Решим уравнение (3.8) и проанализируем его аналитически :

- это уравнение одномодового лазера .

Запишем уравнение (3.8) в следующем виде :
Разделим исходное уравнение на n² .
и введем новую функцию Z :

1/n = n^-1 = Z  Z¹ = - n^-2 следовательно уравнение примет вид :
перепишем его в следующем виде :
разделим обе части данного уравнения на -1 , получим
(3.11)
Уравнение (3.11) - это уравнение Бернулли , поэтому сделаем следующую замену Z = UV , где U и V неизвестные пока функции n , тогда Z¹ = U¹ V + U V¹ .

Уравнение (3.11) , после замены переменных , принимает вид

U¹ V + UV¹ - k UV = k₁

преобразуем , получим

U¹ V + U(V¹ - k V) = k₁ (3.12)

Решим уравнение (3.12)

V¹ - k V = 0  dV/dt = k V

сделаем разделение переменных dV/V =k dt ln V = k t

результат V = e^kt (3.13)

Отсюда мы можем уравнение (3.12) переписать в виде :

U¹ e^kt = k₁

- это то же самое , что dU/dt = k₁e^-kt , dU = k₁e ^-kt dt выразим отсюда U , получим

(3.14)
По уравнению Бернулли мы делали замену Z = U V подставляя уравнения (3.13) и (3.14) в эту замену , получим
Ранее вводили функцию Z = n^-1 , следовательно

(3.15)

Начальное условие n₀=1/(c-k₁/k) , из этого условия мы можем определить константу с следующим образом
Подставляя , найденную нами константу в уравнение (3.15) , получим

(3.16)
Исследуем функцию (3.16) при k = 0 , k < 0 , k > 0 .

При k0 ; e^kt  0 ; (e^kt - 1)0 , то есть (e^kt - 1)k₁/k0 (неопределенность) , раскроем эту неопределенность по правилу Лопиталя . Эту неопределенность вида 0 следует привести к виду . При этом , как и всегда при применении правила Лопиталя , по ходу вычислений рекомендуется упрощать получившиеся выражения , следующим образом :
n(k)_{при k0}  0 , следовательно

Перепишем (3.16) в следующем виде
Линеаризуем нелинейное уравнение , получим
ln n = - kt + c 

Построим график для этих условий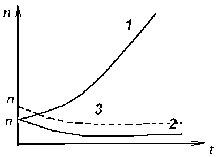


Рис. 3.3 К самоорганизации в одномодовом лазере :

кривая 1 : k < 0 , режим лазерной генерации

кривая 2 : k = 0 , точка бифуркации , порог

кривая 3 : k > 0 , режим лампы.

При k = 0 уравнение (3.8) примет вид
решая его , получим

(3.8)

При условии ; n(t) = const , функция (3.8) приближается к стационарному состоянию , не зависимо от начального значения n₀ , но в зависимости от знаков k и k₁ (смотри рисунок 3.3).


Таким образом , функция (3.8) принимает стационарное решение

3.3. ДИНАМИКА ПОПУЛЯЦИИ .
О распространении и численности видов была собрана обширная информация . Макроскопической характеристикой , описывающей популяцию , может быть число особей в популяции . Это число играет роль параметра порядка . Если различные виды поддерживаются общим пищевым ресурсом , то начинается межвидовая борьба , и тогда применим принцип Дарвина : выживает наиболее приспособленный вид . ( Нельзя не отметить сильнейшую аналогию , существующую между конкуренцией лазерных мод и межвидовой борьбой ). Если имеются однотипные пищевые ресурсы , то становится возможным сосуществование видов . Численность видов может быть подвержена временным колебаниям.

ОДИН ВИД.

Рассмотрим сначала одну популяцию с числом особей в ней n . При наличии пищевых ресурсов А особи размножаются со скоростью :
и гибнут со скоростью :
Здесь k и d - некоторые коэффициенты рождаемости и смертности , в общем случае зависящее от параметров внешней среды обитания . Если бы количество пищи было неограниченно , то эволюционное уравнение выглядело бы так :
Введем обозначение  = kA - d

Оно было бы линейным и описывало бы неограниченный экспериментальный рост (при kA > d), либо экспериментальную гибель (при kA < d) популяции.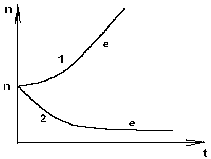



Рис. 3.4 Кривая 1: Экспоненциальный рост ; >0 , kA>d

Кривая 2: Экспоненциальная гибель ; >0 , kA>d.

В общем случае , однако , пищевые ресурсы ограничены , так что скорость потребления пищи
Вместе с тем в общем случае возможно восстановление пищевых ресурсов со скоростью :
Здесь , конечно , рассмотрен придельный случай сохранения полного количества органического вещества

A + n = N = const ,

N - способность среды обитания поддерживать популяцию.

Тогда с учетом A = N - n получится следующее уравнение эволюции популяции одного вида (логистическое уравнение Ферхюльста ) :

(3.17)

Решим уравнение (3.17) аналитически , перепишем его следующим образом

, обозначим kN - d = k₁

Получим :
Воспользуемся табличным интегралом , ,полученное уравнение примет вид :
решим это уравнение , преобразуя

сократим полученное выражение на k , и перенесем переменную k₁ в правую часть , получим
отсюда n(t) 
Начальные условия :
откуда
Подставляя с в решение , получим уравнение в следующем виде
ранее мы обозначали , что , подставляем и преобразуем
сократим на k - коэффициент рождаемости , окончательно получим решение уравнения (3.17)

Итак , получено аналитическое решение логистического уравнения - это решение указывает на то , что рост популяции останавливается на некотором конечном стационарном уровне:
то есть параметр n₁ указывает высоту плато насыщения , к которому стремится n(t) с течением времени .

Параметр n₀ указывает начальное значение численности одного вида популяции : n₀ = n(t₀) . Действительно , ,то есть n₁ - предельная численность вида в данной среде обитания . Иначе говоря , параметр n₁ характеризует емкость среды по отношению к данной популяции . И наконец , параметр (kN - d) задает крутизну начального роста .

Отметим , что при малой исходной численности n₀ (начальное число особи) начальный рост популяций будет почти экспоненциальным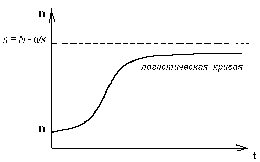



Рис. 3.5. Логистическая кривая.

(эволюция популяции одного вида)

Решение уравнения (3.17) можно представить с помощью логистической кривой (рис. 3.5) . Эволюция полностью детерминирована . Популяция перестает расти , когда ресурс среды оказывается исчерпанным .

Самоорганизация - при ограниченном пищевом ресурсе. Система самоорганизованна и взрывоподобный рост популяции (рис. 3.4 Кривая 1) сменяется кривой с насыщением .

Подчеркнем , что при описании данной биологической системы используют понятийный и физико-математический аппарат из нелинейной неравновесной термодинамики.

Может случится , однако, что всегда за событиями , не управляемыми в рамках модели , в той же среде появится , первоначально в малых количествах , новые виды (характеризуемые другими экологическими параметрами k,N и d) . В связи с такой экологической флуктуацией возникает вопрос о структурной устойчивости : новые виды могут либо исчезнуть , либо вытеснить первоначальных обитателей . Пользуясь линейным анализом устойчивости , не трудно показать , что новые виды вытесняют старые только в том случае , если
Последовательность , в которой виды заполняют экологическую нишу , представлена на рисунке 3.6.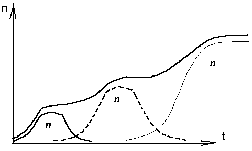



Рис. 3.6. Последовательное заполнение экологической

ниши различными видами .

Эта модель позволяет придать точным количественный смысл утверждению о том , что «выживает наиболее приспособленный» , в рамках задачи о заполнении заданной экологической ниши .
СИСТЕМА «ЖЕРТВА - ХИЩНИК».
Рассмотрим систему, состоящую из двух видов - это «жертва» и «хищник» (например , зайцы и лисицы) , то эволюция системы и ее самоорганизация выглядят иначе , чем в предыдущем случае.

Пусть в биологической системе имеются две популяции - «жертв» - кролики (К) , и «хищников» - лисиц (Л), численностью К и Л .

Проведем теперь рассуждение , которое позволит нам объяснить существование диссипативных структур .

Кролики (К) поедают траву (Т) . Предположим , что запас травы постоянен и неисчерпаем . Тогда , одновременное наличие травы и кроликов способствуют неограниченному росту кроличьей популяции . Этот процесс можно символически изобразить так :

Кролики + Трава  Больше кроликов

К + Т  2К

Тот факт , что в стране кроликов всегда имеется в достатке травы , вполне аналогичен непрерывному подводу тепловой энергии в задаче с ячейками Бенара . Вскоре процесс , в целом , будет выглядеть как диссипативный (во многом аналогично процессу Бенара ).

Реакция « Кролики - Трава » происходит спонтанно в направлении увеличения популяции кроликов, что является прямым следствием второго начала термодинамики .

Но вот в нашу картину , где мирно резвятся кролики , прокрались хищные лисицы (Л), для которых кролики являются добычей . Подобно тому , как по мере поедания травы кроликов становится больше , за счет поедания кроликов возрастает число лисиц :

Лисицы + Кролики  Больше лисиц

Л + К  2Л

В свою очередь лисицы , как и кролики являются жертвами - на этот раз человека , точнее говоря происходит процесс

Лисицы  Меха

Конечный продукт - Меха , не играет непосредственной роли в дальнейшем ходе процесса . Этот конечный продукт можно , однако , рассматривать как носитель энергии, выводимой из системы , к которой она была в начале подведена (например, в виде травы ).

Таким образом , в экологической системе также существует поток энергии - аналогично тому , как это имеет место в химической пробирке или биологической клетке .

Совершенно ясно , что в действительности происходят периодические колебания численности популяции кроликов и лисиц , причем за нарастании численности кроликов следует нарастание численности лисиц , которые сменяются уменьшением численности кроликов , сопровождающимся столь же резким снижением численности лисиц , затем повышенным подъемом численности кроликов и так далее (рис. 3.7).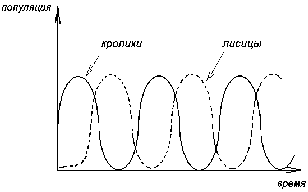



Рис. 3.7. Изменение численности популяций кроликов и лисиц

со временем. Наличие периодичности означает

возникновение экологической структуры.

С течением времени численность обеих популяций меняется в соответствии с последовательным прохождением точек графика . Через некоторое время (конкретное значение зависит от быстроты поедания лисицами кроликов , а так же от скорости размножения обоих видов) весь цикл начинается вновь.

Поведение популяций при различных степенях плодовитости , а так же различных способностях избегать истребления можно изучить количественно с помощью программы : ПОПУЛЯЦИЯ (в приложении).

Эта программа реализует решение уравнений для диссипативной структуры «кролики - лисицы». Результат решения изображается графически . Решается система дифференциальных уравнений
Здесь буквы К, Л, Т - означают соответственно количество кроликов , лисиц , травы ; коэффициенты k₁, k₂, k₃ - обозначают соответственно скорость рождения кроликов , скорость поедания кроликов лисицами и скорость гибели лисиц.

В программе понадобится уточнить значение отношений