Яничкина Е.А. МО-20 курсовая работа ТИ. Первое высшее техническое учебное заведение
 Скачать 428.04 Kb. Скачать 428.04 Kb.
|
2.6 Восстановление сигнала измерительной информацииВ реальных условиях точного восстановления непрерывной функции невозможно из-за того, что не может быть выполнена теорема Котельникова. На рисунках 2.6.1, 2.6.2 и 2.6.3 представлены восстановленные сигналы дискретные по времени и уровню при различных частотах среза. 1. 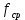 =f ∆t= =f ∆t=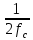 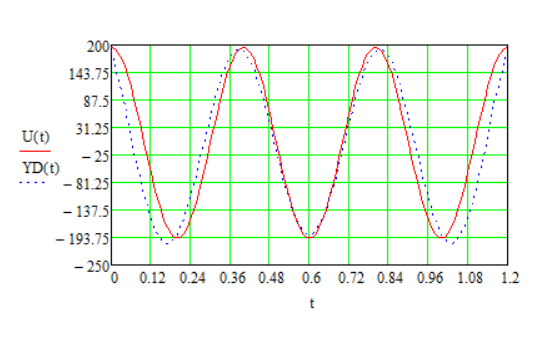 Рис. 2.6.1 – восстановленный сигнал дискретный по времени и уровню 2. 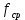 =2f t=0,5∆t =2f t=0,5∆t 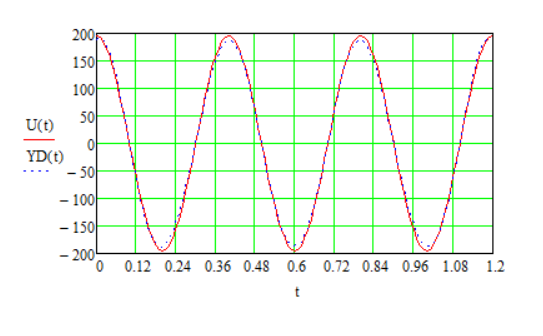 Рис. 2.6.2 – восстановленный сигнал дискретный по времени и уровню 3. 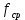 =4/3f t=0,75∆t =4/3f t=0,75∆t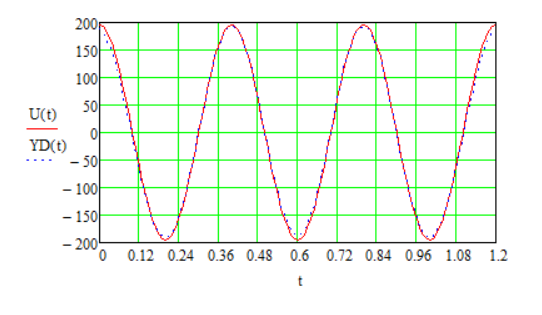 Рис. 2.6.1 – восстановленный сигнал дискретный по времени и уровню Особенностью сигнала, дискретизированного в соответствие с теоремой Котельникова является то, что он может быть восстановлен с помощью фильтра нижних частот. Следовательно, если дискретизированный с шагом 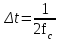 сигнал х(t)диск. подать на вход идеального фильтра с верхней границей пропускания сигнал х(t)диск. подать на вход идеального фильтра с верхней границей пропускания 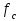 , то на выходе получается восстановленный без погрешностей непрерывный сигнал х(t) (Рисунок.2.6.4). , то на выходе получается восстановленный без погрешностей непрерывный сигнал х(t) (Рисунок.2.6.4). Рис. 2.6.4 – восстановленный без погрешностей непрерывный сигнал х(t) 2.7 ВыводыБыло рассмотрено кодирование информационного сигнала и его квантования по уровню, подготовлена измерительная информация для передачи по каналу связи с использованием двоичной фазовой модуляции, для чего были использованы расчёты характеристик этого канала. После демодуляции было произведено восстановление сигнала. Важной частью при кодировании была защита информации от ошибок. 3 ИССЛЕДОВАНИЕ ОШИБОК3.1 Общая характеристика ошибок при дискретизации по времени и квантованию по уровню сигналовСуществует два основных источника ошибок. Один из них – дискретизация, в процессе которой выбирают значение сигнала в дискретный момент времени и затем удерживают его до момента формирования следующего отсчета. Второй источник ошибок возникает как следствие работы квантователя. Значение отсчета подтягивается либо опускается до своего ближайшего возможного уровня квантования. Разность между истинным значением сигнала и его квантованным приближением называют ошибкой или шумом квантования.  Чем больше число разрешенных уровней, тем меньше величина ошибки или шумов квантования. Имеем зону квантования и зону ограничения. Соответственно различают шумы квантования и шумы ограничения. Для того, чтобы избавиться от шумов ограничения, нужно принять меры для предотвращения перегрузки кантователя. Один из способов уменьшения ошибок – увеличение количества уровней квантования или уменьшение шага дискретизации. Это, без сомнения, в ряде случаев уменьшит ошибку, поскольку любой отсчет будет располагаться ближе к соседним уровням квантования, чем в случае меньшего количества уровней. 3.2 Исследование ошибок при квантовании сигнала по уровню и дискретизации по времениШум квантования возникает при оцифровке сигнала, так как аналогово-цифровой преобразователь имеет конечную разрядность, то есть шкала измерения не является непрерывной. Если значение напряжения не равняется в точности одному из возможных значений АЦП, то значение аналогового напряжения округляется в ту или иную сторону, в зависимости от типа и принципа работы АЦП, но в любом случае возникает ошибка при оцифровке, то есть значение, выданное АЦП в действительности, не соответствует исходному аналоговому значению. Эту разницу просто рассматривают как некую помеху или шум. Отношение сигнал/шум на выходе квантователя:  N – количество разрядов = 4  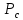 – мощность сигнала – мощность сигнала 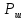 - мощность шума - мощность шума  Таблица 3.2.1 – зависимость ошибки от частоты среза
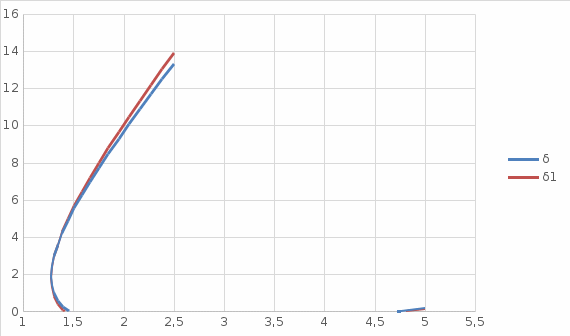 Рис.3.2.1 – зависимость ошибки от частоты среза 3.3Предложения по выбору критерия отсчетов при дискретизации сигнала по времениГрафик периода дискретизации от 0,5 до 0,75 погрешность изменяется не существенно. В зависимости от точности восстановления сигнала мы выбираем частоту. 3.4 ВыводыВыбор частоты дискретизации (период дискретизации) зависит от точности, с которой требуется восстановить исходный передаваемый сигнал по дискретным отсчетам. Из графиков видно, что максимальная ошибка восстановления передаваемого сигнала составляет 1 c, а минимальная 0,75 c. Поэтому, задавшись максимальной ошибкой восстановления можно определить период (частоту) дискретизации сигнала. ЗАКЛЮЧЕНИЕВ курсовой работе был рассмотрен заданный сигнал с помощью исходных данных для дискретизации по времени и квантования по уровню сигнала измерительной информации, исходных данных для кодирования, защиты и выбора вида модуляции передающей информации, исходных данных для расчета характеристик канала связи передающей измерительной информации мы рассмотрели сигнал. В расчетно-исследовательской части: Произведено квантование по уровню и кодирование информации, защита сигнала от ошибок, подготовлена измерительная информация для передачи по каналу связи с использованием двоичной фазовой модуляции, рассчитаны характеристики канала связи, рассмотрены понятия демодуляция и декодирование информации для нашего сигнала, восстановлен сигнал измерительной информации. СПИСОК ЛИТЕРАТУРЫВентцель Е.С. Теория вероятностей: Учебник для вузов. ‑ 6-е изд., стереотип. – М.: Высш. школа, 1999 – 576 с. Теория информации: методические указания к практическим занятиям/И.И. Сытько, Д.А. Кремчеева, Э.А. Кремчеев, СПб: Лема, 2018, 22 с. Панин В.В. Основы теории информации: учебное пособие для вузов. - 3 изд. испр. - М.: БИНОМ. Лаборатория знаний, 2011. Соболь Б.В., Галин А.Б., Панов Ю.В., Рашидова Е.В., Садовой Н.Н. Информатика. Учебник. - Издание 3, дополн. иперераб. - Ростов н/Д: Феникс, 2010. Андреев Е.В., Щепин Е.В. Основы теории информации. Учебное пособие. Информатика №4 - 2014. Хохлов Г.И. Основы теории информации. Учебное пособие для вузов.Высшее профессиональное образование, - Москва: Академия, 2010. Грановский В.А. Системная метрология: метрологические системы и метрология систем. – СПб.: ГНЦ РФ ЦНИИ “Электроприбор”, 1999. – 360 с. Харт Х. Введение в измерительную технику: Пер. с нем. – М.: Мир, 1999. – 391 с. Дмитриев В.И. Прикладная теория информации. Учебник – М.: Высшая школа,1989. – 245 c. |