Задание 1. Коновалова Е.О. Программа среднего профессионального образования Специальное дошкольное образование. Дисциплина Математика
 Скачать 68.95 Kb. Скачать 68.95 Kb.
|
|
АНО ПО «Открытый социально-экономический колледж» г. Тула, ул. Менделеевская, дом 1. Программа среднего профессионального образования «Специальное дошкольное образование». Дисциплина: Математика. Практическое задание №1. Выполнил: слушатель Коновалова Екатерина Олеговна. Преподаватель: Васильцова Анна Сергеевна.  а) 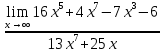 Вынесем за скобки старшие степени по х в числителе и знаменателе: 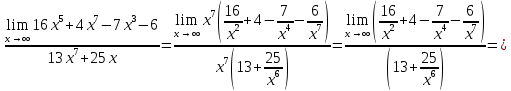 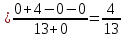 б) 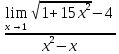 Умножим и разделим выражение на 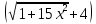 , чтобы получить разность квадратов в числителе: , чтобы получить разность квадратов в числителе: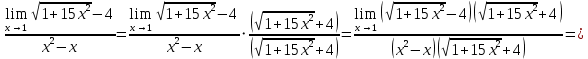 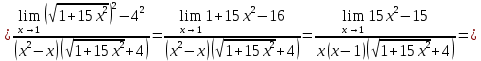 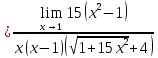 Теперь применим формулу разности квадратов в числителе: 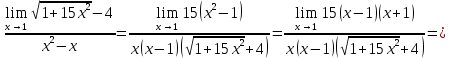 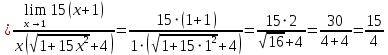 в) 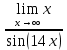 Т.к. в знаменателе стоит ограниченная функция 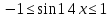 , причем знакопеременная, а в числителе бесконечно большая при , причем знакопеременная, а в числителе бесконечно большая при 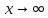 функция, заданный предел неопределенный: функция, заданный предел неопределенный: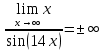 Примечание: скорее всего предел должен быть таким: 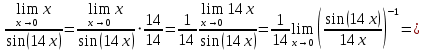 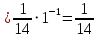 Здесь воспользовались первым замечательным пределом 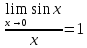 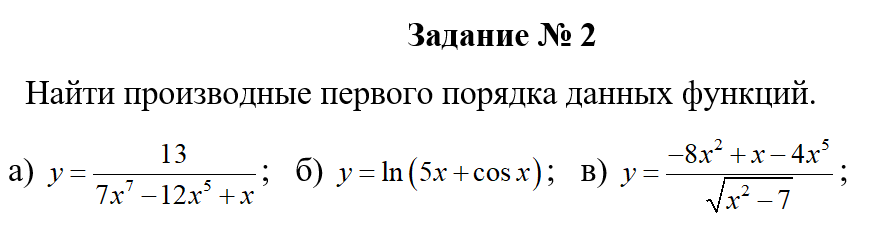 а) 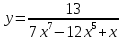 Представим функцию в виде степенной: 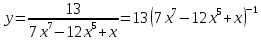 И применим правило дифференцирования сложной функции и суммы функций: 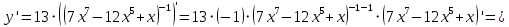 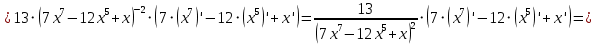 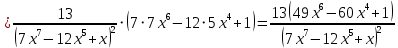 б) 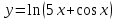 Применим правила дифференцирования сложной функции и суммы функций: 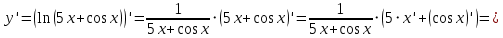 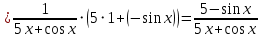 в) 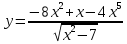 Применим правила дифференцирования частного и сложной функции: 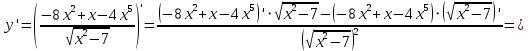 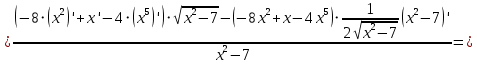 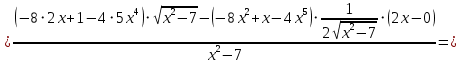 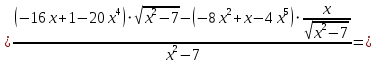 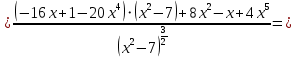 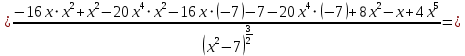 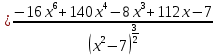 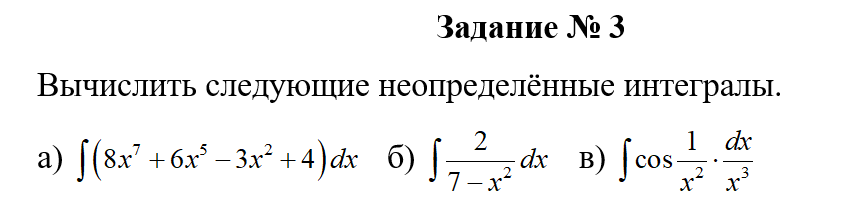 Вычислить следующие неопределенные интегралы: а) 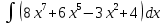 Используем свойство линейности и применим непосредственное интегрирование: 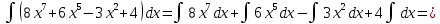 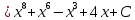 б) 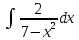 Разложим подынтегральное выражение на сумму простейших дробей с помощью метода неопределенных коэффициентов: 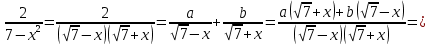 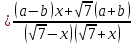 Приравняем коэффициенты при различных степенях х: 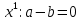 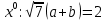 Отсюда: 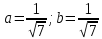 Искомое разложение: 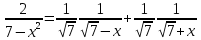 Найдем интеграл: 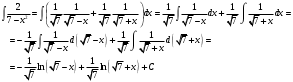 в) 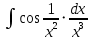 Заметим, что 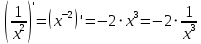 Внесем 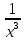 под знак дифференциала: под знак дифференциала: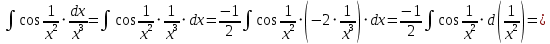 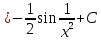 |
