Сэндвичи. Сэндвиси Жаннет Гурман (1). Программам b a 11. 07. 21 Курс методы оптимизации в управлении задание 1
 Скачать 320.92 Kb.
|
Курс: МЕТОДЫ ОПТИМИЗАЦИИ В УПРАВЛЕНИИ Задание № 1 Электронную копию задания №1, а также следующее задание №2, можно взять на www.hcxl.net/mba16.html по номеру варианта. Задание №3 - собственный проект. Вариант 004 1:1 Сэндвичи Жаннет ГурманЖаннет Гурман продает сэндвичи строителям и заводским рабочим в обеденный перерыв со своего собственного грузовичка. Ее сэндвичи пользуются особой популярностью, поскольку она закупает свежие продукты у местных поставщиков каждое утро. Необходимые для ее бизнеса продукты приведены в таблице.
В дополнении к $420, которые она тратит на эти продукты, Жаннет тратит в среднем $280 ежедневно, на бензин, обслуживание грузовика, страховку, и зарплату помощникам. Жаннет с помощниками каждое утро нарезает мясо и сыр кусочками по 1 унции, делает сэндвичи, заворачивает их в тонкую полиэтиленовую пленку и складывает в грузовичок. Грузовичок может вместить до 300 сэндвичей, причем практика показывает, что она может продать все эти сэндвичи. В таблице приведены цены и ингредиенты (в унциях) для всех ее сэндвичей. 1 фунт=16 унций
Сколько сэндвичей каждого типа следует готовить, чтобы максимизировать доход? Какова чистая прибыль Жаннет (до уплаты налогов) за год, если она работает 200 дней в году? Жаннет рассматривает возможность закупки дополнительно еще одного куска какого- либо мяса или сыра от тех же поставщиков. Если только один дополнительный кусок будет закупаться, что именно выгоднее всего закупить Жаннет? Увеличение какого ресурса наиболее выгодно для Жаннет? Насколько чувствительно оптимальное решение к изменению цен за один сэндвич? Как измениться решение, при изменении цен на каждый вид продукции? Как изменится решение если цены на все сэндвичи увеличить на $1, $2, $10? Почему? Решение: А) Определим цель задачи и вид целевой функции. В данном случае необходимо максимизировать доход, следовательно целевая функция должна вычислять полный доход. Полный доход будет определяться количеством сэндвичей каждого вида, которые будут произведены и проданы. Тогда, в качестве переменных задачи следует выбрать количества сэндвичей каждого вида, которые следует произвести и продать. В задаче их будет пять в соответствии с номенклатурой производства сэндвичей. При этом целевая функция будет иметь вид: Р = 2,75*Х1 + 3,50*х2 + 3,25*Х3 + 4,00*Х4 + 4,25*Х5 ($). На следующем этапе необходимо выяснить, при каких ограничениях нужно найти максимальный доход. В данном случае из условия задачи следует, что можно произвести и продать не более 300 сэндвичей в день. Также известно, что затраты на ингредиенты за день должны быть не более 420 долл., а также накладные затраты – не более 280 долл. Кроме того, расход ингредиентов для производства сэндвичей не может превышать их максимально возможный запас, который определяется количеством закупаемых ингредиентов: 1) 3 шт. 8-фунтовых запеченных грудки индюшек; 2) 3 шт. 12-фунтовых куска жареной говядины; 3) 3 шт. 10-фунтовых куска ветчины; 4) 3 шт. 8-фунтовых головки швейцарского сыра; 5) 300 шт. булочек для сэндвичей. Для расчета масимально возможного запаса ингредиентов составим таблицу 1. Таблица 1 – Расчет максимально возможного запаса и стоимости ингредиентов
На основании имеющихся данных сформируем данные для расчета максимального дохода от продажи сэндвичей. В таблице 2 показаны результаты применения функции Поиска решений при заданных ограничениях. Таблица 2 – Результаты вычисления максимального дохода от продажи сэндвичей
Соблюдение ограничений по максимально возможному расходу ингредиентов подтверждается данными таблицы 3. Таблица 3 – Показатели использования ингредиентов для производства
Прибыль от реализации до уплаты налогов по результатам выполнения сформированной производственной программы при условии работы 200 дней в году составит 67200 долл. (таблица 4). Таблица 4 – Расчет прибыли до уплаты налогов от производства сэндвичей
Для того чтобы выяснить, запас какого из дефицитных ресурсов выгоднее увеличивать в первую очередь, необходимо определить, какую пользу (например, прибыль) принесет увеличение запасов каждого из них на единицу. Для этих целей вводится понятие ценности дополнительной единицы i-го ресурса (теневая цена):  .То есть сначала наращивается запас ресурса, имеющего максимальное значение  , затем – второе по величине и т.д.Проведем анализ чувствительности задачи о сэндвичах. Для этого необходимо после запуска в Excel задачи на решениев окне "Результаты поиска решения" выделить с помощью мыши два типа отчетов: "Результаты" и "Устойчивость"(рис. 1).  Рисунок 1 - Выделение типов отчетов требуемых для анализа чувствительности Отчет по результатам Отчет по результатам состоит из трех таблиц (рис. 2): 1) таблица 5 содержит информацию о ЦФ; 2) таблица 6 содержит информацию о значениях переменных, полученных в результате решения задачи; 3) таблица 7 показывает результаты оптимального решения для ограничений и для граничных условий. 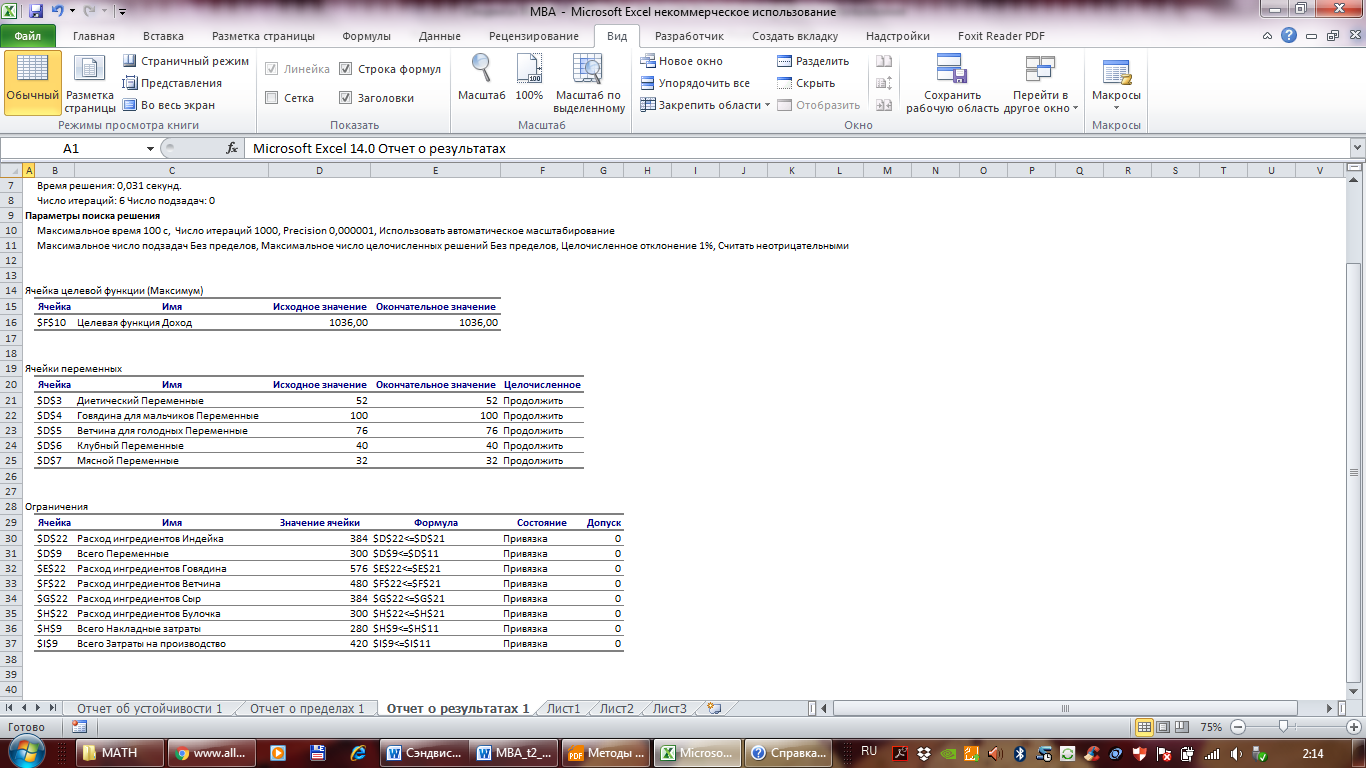 Рисунок 2 - Лист отчета по результатам Если ресурс используется полностью (то есть ресурс дефицитный), то в графе "Статус" ("Состояние") соответствующее ограничение указывается как "привязка"; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается "не связан". В графе "Значение" приведены величины использованного ресурса. Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Так, если на ресурс наложено ограничение типа  , то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. По условию нашей задачи все ресурсы используются полностью, т.е. являются дефицитными. Поэтому в графе допуск не отражено остатков ресурса. На основании проведенного анализа можно сделать вывод о том, что существуют причины (ограничения), не позволяющие производить большее количество сэндвичей и получать большую прибыль. Проанализировать эти причины позволяет отчет поустойчивости (таблица 5). Нормированная стоимость, которая показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Однако, в отчете по устойчивости для рассматриваемой задачи нормированная стоимость для всех видов сэндвичей равна 0 (таблица 5). Это означает, что если мы, несмотря на оптимальное решение, потребуем включить в план выпуска какой-либо вид продукта, то новый план выпуска не изменит оптимальную прибыль от производства. Таблица 5 – Отчет по устойчивости
В таблице 5 Предельные значения приращения ресурсов  . В графе "Допустимое Уменьшение" показывают, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптимальное решение. Рассмотрим анализ дефицитных ресурсов.Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие выпускать большее, чем в оптимальном решении, количество сэндвичей и получать более высокую прибыль. В рассматриваемой задаче такими ограничениями являются все виды дефицитных ресурсов. Поскольку знак ограничений этих ресурсов имеет вид  , то возникает вопрос, на сколько максимально должна возрасти емкость их запаса, чтобы обеспечить увеличение выпуска сэндвичей. Ответ на этот вопрос показан в графе "Допустимое Увеличение". Запас индейки имеет смысл увеличить самое большее на 274 унции, запас говядины – на 249 унций, сыра – на 70 унций. Это приведет к новым оптимальным решениям, увеличивающим доход и прибыль по сравнению с первоначальными значениями. Дальнейшее увеличение запасов ингредиентов сверх указанных пределов не будет больше улучшать решение, т.к. уже другие ресурсы станут связывающими. Ценность дополнительной единицы i-го ресурса (теневая цена) рассчитывается только для дефицитных ресурсов. Чтобы определить, какой ресурс выгоднее всего расширять, необходимо принять во внимание показатели «Теневая цена». Увеличение количества булочек приведет к получению дополнительно 1,07 дол. прибыли, сыра – на 0,13 долл., говядины – на 0,10 долл. Очевидно, что наиболее выгодным будет увеличение запасов булочек. Методы оптимизации в управлении – Варюхин С.Е. 2016 г. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
