Расчет вертикального одноступенчатого цилиндрического редуктора. Вариант 2-5. Расшифровка подписи Члены комиссии подпись расшифровка подписи
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
2.3 Проектный расчет передачи2.3.1 Межосевое расстояние 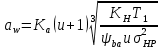 Где Ка=410 для косозубых передач. Примем коэффициент ширины зубчатого венца для косозубой передачи ψba=0,400. На этапе проектного расчета задаемся значением коэффициента контактной нагрузки KH=1,2. Тогда: 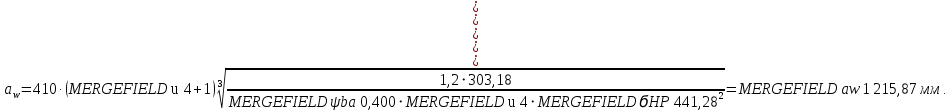 Полученное межосевое расстояние округлим до ближайшего большего стандартного значения aw=224 мм. 2.3.2 Модуль, числа зубьев колес и коэффициенты смещения Рекомендуемый диапазон для выбора модуля:  Из полученного диапазона выбираем стандартный модуль mn = 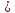 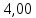 мм. мм.Суммарное число зубьев передачи: 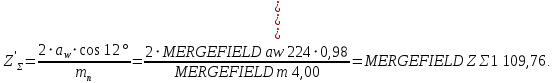 Полученное значение 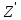 округлим до ближайшего целого числа Z∑ = 110 и определим делительный угол наклона зуба: округлим до ближайшего целого числа Z∑ = 110 и определим делительный угол наклона зуба: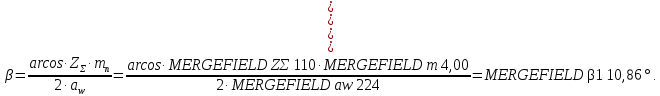 Число зубьев шестерни: 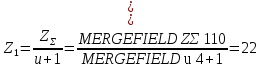 Число зубьев колеса: 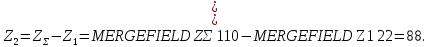 Фактическое передаточное число: 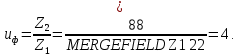 При u < 4,5 отличие фактического передаточного числа от номинального должно быть не больше 2,5%. 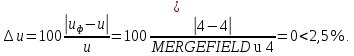 Учитывая, что Z1>17, принимаем коэффициент смещения x1=0, x2=0 2.3.3 Ширина зубчатых венцов и диаметры колес Ширина зубчатого венца колеса: 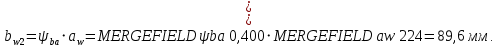 Округлим bw2 до ближайшего числа из ряда нормальных линейных размеров bw2=90 мм. Ширину зубчатого венца шестерни bw1 примем bw1=95 мм. Определим диаметры окружностей зубчатых колес: -делительные окружности: 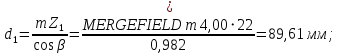 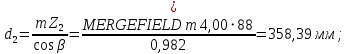 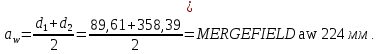 -окружности вершин зубьев 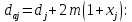 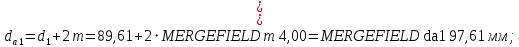 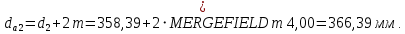 -окружности впадин зубьев 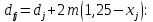 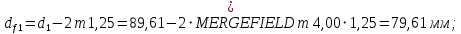 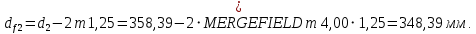 2.3.4 Окружная скорость в зацеплении и степень точности передачи 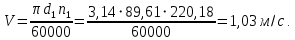 Для полученной скорости назначим степень точности передачи nст=8, учитывая, что nст=9 для закрытых зубчатых передач применять не рекомендуется. 2.4 Проверочный расчет передачи2.4.1 Проверка контактной прочности зубьев Используем формулу: 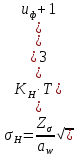 где Zσ=8400 для косозубых передач. Коэффициент контактной нагрузки: 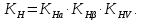 Коэффициент неравномерности распределения нагрузки между зубьями: 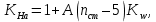 где А=0,15 для косозубых передач, Kw – коэффициент, учитывающий приработку зубьев. При НВ2 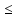 350 используем формулу: 350 используем формулу: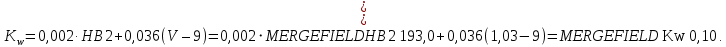 Тогда: 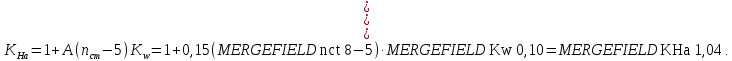 Коэффициент неравномерности распределения нагрузки по ширине колеса: 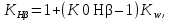 где K0Hβ – коэффициент неравномерности распределения нагрузки в начальный период работы. Для определения K0Hβ найдем коэффициент ширины венца по диаметру: 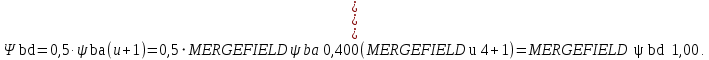 По значению Ψbdопределим K0Hβ= 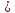 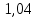 .Тогда: .Тогда: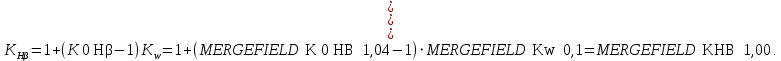 Динамический коэффициент KHV= 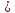 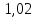 определим методом линейной интерполяции. определим методом линейной интерполяции.Окончательно найдем: 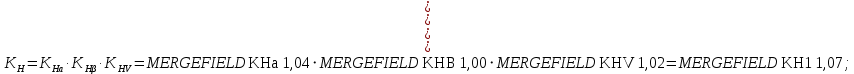 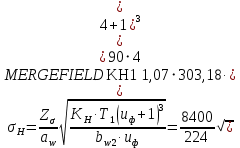 2.4.2 Проверка изгибной прочности зубьев Напряжения изгиба в зубе шестерни: 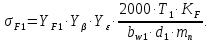 Коэффициент формы зуба при xj=0: 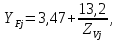 где 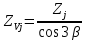 – эквивалентное число зубьев. – эквивалентное число зубьев.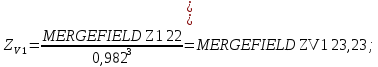 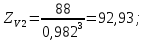  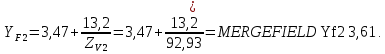 Коэффициент, учитывающие влияние угла наклона зуба на его прочность: 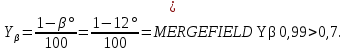 Коэффициент торцевого перекрытия: 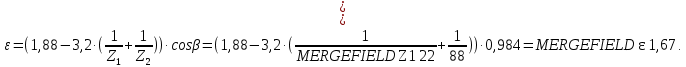 Коэффициент, учитывающие перекрытие зубьев: 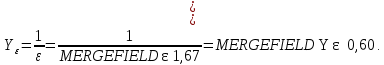 Коэффициент нагрузки при изгибе: 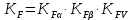 Для определения его коэффициентов используем зависимости: 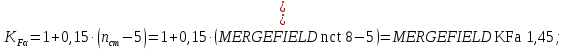 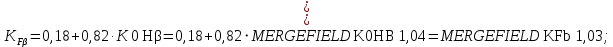 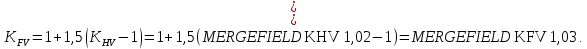 Тогда: 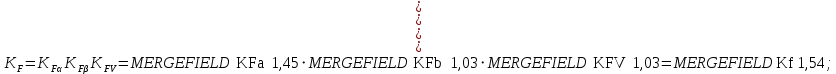 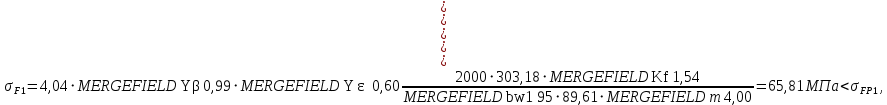 где 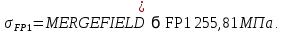 Напряжение в зубьях колеса: 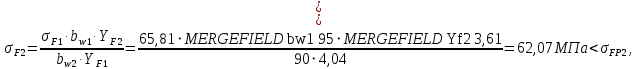 где 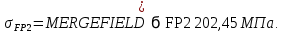 |
