|
1. Вычисляем математическое ожидание для каждого образа. Для образа Модельера№1:
Для образа Модельера№2:
2. Вычисляем также для каждого образа матрицу ковариаций.
Матрица ковариации для образа Модельера№1:
6.1905
|
-1.9642
|
-1.9642
|
8.8598
|
Матрица ковариации для образа Модельера№2:
11.7060
|
0.9534
|
0.9534
|
8.7705
|
3. Вычисляем среднюю и обратную матрицы ковариаций:
Средняя матрица ковариации:
9.6377
|
-0.1407
|
-0.1407
|
187.08
|
Обратная матрица ковариации:
0.1038
|
0.0017
|
0.0017
|
0.1136
|
4. Вычисляем коэффициенты 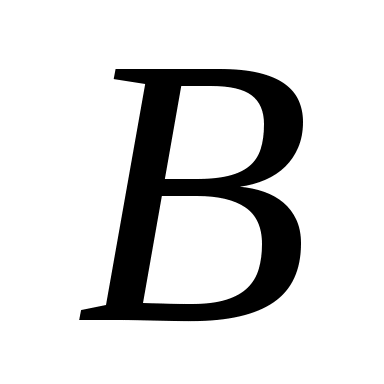 и и 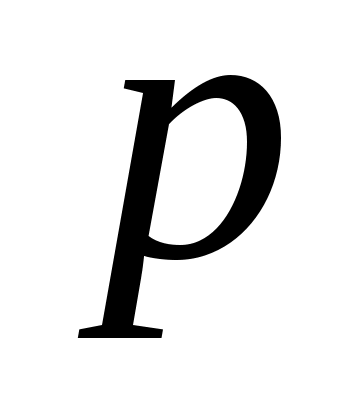 . .
-
B
|
|
P
|
-1.0520
|
|
122.2351
|
-1.1836
|
|
|
5. Вычисляем дискриминантную функцию, проводим распознавание на всех объектах и вычисляем ошибки 1-го и 2-го рода на материале обучения. В табл. 3 приведены результаты вычислений.
табл. 3
-
|
Талия
|
Вес
|
N
|
D(x)
|
Распозн.
|
Ошибки
|
1
|
51
|
47
|
1
|
13.3275
|
1
|
0
|
2
|
56
|
44
|
1
|
8.1093
|
1
|
0
|
3
|
56
|
43
|
1
|
18.1348
|
1
|
0
|
4
|
57
|
47
|
1
|
22.2780
|
1
|
0
|
5
|
59
|
47
|
1
|
14.4668
|
1
|
0
|
6
|
55
|
47
|
1
|
26.5393
|
1
|
0
|
7
|
56
|
47
|
1
|
6.8270
|
1
|
0
|
8
|
54
|
44
|
1
|
9.6991
|
1
|
0
|
9
|
56
|
43
|
1
|
13.7698
|
1
|
0
|
10
|
60
|
50
|
1
|
4.6093
|
1
|
0
|
11
|
52
|
50
|
1
|
11.6270
|
1
|
0
|
12
|
54
|
45
|
1
|
13.3840
|
1
|
0
|
13
|
57
|
44
|
1
|
12.1702
|
1
|
0
|
14
|
56
|
41
|
1
|
15.7472
|
1
|
0
|
15
|
57
|
48
|
1
|
10.6033
|
1
|
0
|
16
|
64
|
51
|
2
|
-3.9215
|
2
|
0
|
17
|
63
|
54
|
2
|
-16.8710
|
2
|
0
|
18
|
63
|
52
|
2
|
-16.8191
|
2
|
0
|
19
|
69
|
59
|
2
|
-12.1759
|
2
|
0
|
20
|
62
|
54
|
2
|
-9.2201
|
2
|
0
|
21
|
69
|
52
|
2
|
-14.5347
|
2
|
0
|
22
|
69
|
52
|
2
|
-10.7409
|
2
|
0
|
23
|
64
|
58
|
2
|
-14.6112
|
2
|
0
|
24
|
60
|
52
|
2
|
-7.6046
|
2
|
0
|
25
|
61
|
50
|
2
|
-3.7493
|
2
|
0
|
26
|
61
|
58
|
2
|
-14.3991
|
2
|
0
|
27
|
60
|
55
|
2
|
-10.7634
|
2
|
0
|
28
|
70
|
59
|
2
|
-11.0074
|
2
|
0
|
29
|
67
|
57
|
2
|
-21.9980
|
2
|
0
|
30
|
63
|
53
|
2
|
-15.8513
|
2
|
0
|
31
|
64
|
54
|
2
|
-15.9273
|
2
|
0
|
32
|
70
|
57
|
2
|
-10.7339
|
2
|
0
|
33
|
68
|
50
|
2
|
-8.6306
|
2
|
0
|
34
|
62
|
59
|
2
|
-8.9184
|
2
|
0
|
35
|
68
|
59
|
2
|
-14.2051
|
2
|
0
|
36
|
70
|
54
|
2
|
-14.2098
|
2
|
0
|
37
|
61
|
59
|
2
|
-15.8424
|
2
|
0
|
38
|
69
|
57
|
2
|
-20.1851
|
2
|
0
|
39
|
66
|
52
|
2
|
-24.5711
|
2
|
0
|
40
|
69
|
53
|
2
|
-17.9967
|
2
|
0
|
41
|
68
|
46
|
0
|
|
2
|
|
42
|
67
|
47
|
0
|
|
1
|
|
43
|
51
|
51
|
0
|
|
2
|
|
44
|
57
|
44
|
0
|
|
2
|
|
45
|
60
|
56
|
0
|
|
1
|
|
46
|
58
|
45
|
0
|
|
1
|
|
47
|
58
|
46
|
0
|
|
1
|
|
48
|
68
|
49
|
0
|
|
2
|
|
49
|
69
|
55
|
0
|
|
1
|
|
50
|
69
|
55
|
0
|
|
1
|
|
51
|
53
|
44
|
0
|
|
1
|
|
52
|
66
|
49
|
0
|
|
1
|
|
53
|
69
|
45
|
0
|
|
2
|
|
54
|
54
|
59
|
0
|
|
2
|
|
55
|
58
|
60
|
0
|
|
2
|
|
56
|
57
|
41
|
0
|
|
1
|
|
57
|
60
|
52
|
0
|
|
1
|
|
58
|
50
|
54
|
0
|
|
2
|
|
59
|
66
|
57
|
0
|
|
2
|
|
60
|
55
|
52
|
0
|
|
1
|
|
Таким образом, для данной задачи распознавание с помощью алгоритма Дискриминантная функция дало нулевую ошибку 1-го и 2-го рода.
Графическая иллюстрация к данной задаче представлена на рис. 5.
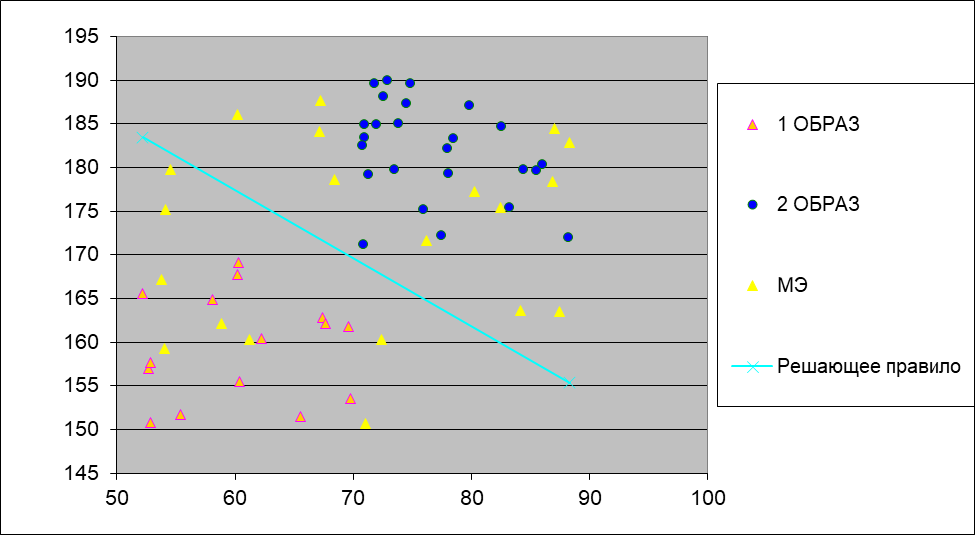
рис. 5 |
 Скачать 0.76 Mb.
Скачать 0.76 Mb.
