Инж. инж мех (копия). Статика Бос жне бос емес дене. Байланыстар жне оларды реакциялары. Жиі кездесетін байлансытар трлері. Босату принципі
 Скачать 1.78 Mb.
|
|
Эйлер-Даламбер теоремасы: АҚДның бекітілген нүктеге қатысты кез-келген орын ауыстыруын осы бекітілген нүкте арқылы өтетін, шекті бұру өсі деп аталатын белгілі бір өске қатысты бұру арқылы жүзеге асыруға болады. Қорытынды: АҚД-ның бекітілген нүктеге қатысты қозғалысын осы нүкте арқылы өтетін лездік айналу өстеріне қатысты шексіз аз бұрылулардың үздіксіз жиынтығы деп қарастыруға болады. 8. Нүктенің күрделі қозғалысы. Нүктенің салыстырмалы, тасымалдау және абсолют қозғалыстары. Нүктенің салыстырмалы, тасымалдау және абсолют жылдамдықтары мен үдеулері. Нүктенің күрделі қозғалыстағы жылдамдықтарды қосу туралы теоремасы . Егер нүкте екі немесе одан артық қарапайым қозғалыстарға қатысса, онда нүктенің қозғалысын күрделі қозғалыс деп атаймыз. Мысалы, ұшақтың, кеменің, трамвайдың ішінде кісінің жүруі күрделі қозғалыс болады, өйткені ол, біріншіден, ұшақтың, кеменің, трамвайдың ішінде қозғалады, екіншіден, ұшақпен, кемемен, трамваймен бірге жерге қатысты қозғалады. Судың бетімен келе жатқан қайық та күрделі қозғалыста болады. Ол, біріншіден, суға қатысты қозғалыста, екіншіден, судың жағаға қатысты қозғалысында болады. Салыстырмалы қозғалыс — нүктенің (немесе дененің) шартты түрде жылжымайтын деп алынған Oxyz санақ жүйесіне қатысты орын ауыстыратын жылжымалы Oxyz санақ жүйесімен салыстырғандағы қозғалысы. Нүктенің тасымал қозғалысы - өске қатысты пластинкамен бірге бұрыштық жылдамдықпен айналуы. Нүктенің абсолют қозғалысы тасымал және салыстырмалы қозғалыстардан құралады. Дененің тасымал қозғалысының өзі күрделі қозғалыс. Жалпы жағдайда, МD нүкте “О” полюспен бірге ілгерілемелі және полюсқа қатысты айналма қозғалыста болады. Нүктенің абсолют қозғалысы  (а)теңдеуімен беріледі. Олай болса абсолют жылдамдық . (1) Теорема. Нүктенің абсолют жылдамдығы оның тасымал және салыстырмалы қозғалыс жылдамдықтарының геометриялық қосындысына тең. 9. Нүктенің күрделі қозғалыстағы үдеулерді қосу туралы теоремасы. Кориолис теоремасы. Кориолистік үдеуінің шамасы және бағыты. Кориолистік үдеуінің физикалық мағынасы. Нүктенің абсолют үдеуін табу үшін абсолют жылдамдықтан уақыт бойынша туынды аламыз. Сонда  мұндағы  - Кориолис немесе бұру үдеуі деп аталады, яғни нүктенің Кориолис үдеуі тасымал қозғалыстың бұрыштық жылдамдығы мен салыстырмалы жылдамдықтың екі еселенген векторлық көбейтіндісіне тең. Кориолис удеуі векторының бағыты және векторлары арқылы өтетін жазықтыққа перпендикуляр.Кориолис теоремасы - егер дененің тасымал қозғалысы айналмалы болса, онда абсолюттік үдеу салыстырмалы, тасылмал және кориолистік үдеулерінің векторлық қосындысына тең. Кориолис удеуі векторының бағытын анықтау үшін салыстырмалы жылдамдық векторын тасымал бұрыштық жылдамдық векторына перпендикуляр жазықтыққа проекциялап, осы проекцияны дененің айналу бағытында -қа бұру қажет. Кориолис үдеуінің модулі  , (4)мұндағы - және векторларының арасындағы бұрыш. Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. 10. Абсолют қатты дененің жазық параллель қозғалысының теңдеуі. Ілгерілемелі және полюсты айналу қозғалыстарға жіктеу. Абсолют қатты дене (АҚД)деп кез-келген екі нүктесінің ара қашықтығы үнемі тұрақты сақталатын, яғни геометриялық формасын өзгертпей сақтайтын денені айтады. Жазық параллель қозғалыс кезінде АҚД-ның барлық нүктелері негізгі деп аталатын жазықтыққа параллель қозғалады.  Қатты дененің ілгерілемелі қозғалысы деп оның әрбір екі нүктесін қосатын түзулердің кез-келгені өзіне-өзі тек параллель қозғалатындай қозғалыс түрін айтамыз. 11. Жазық фигура нүктесінің жылдамдығын полюс арқылы анықтау. Дененің екі нүктесі жылдамдықтарының проекциялары туралы теорема. Жазық фигура нүктесінің үдеуін полюс арқылы анықтау. Сонымен, жазық фигураның кез-келген М нүктесінің жылдамдығы геометриялық түрде полюсте қабылданған басқа А нүктесінің жылдамдығынан және осы полюстің айналасында фигураның айналуы кезінде М нүктесі алатын жылдамдықтан тұрады. Теорема:осы нүктелер арқылы өтетін оське жазық фигураның екі нүктесінің жылдамдығының проекциясы тең. Vmx = Vax немесе V MA cosβ =VA cosα. Жылдамдықтардың жедел орталығы. Осылайша, жазық фигураның кез-келген М нүктесінің үдеуі геометриялық түрде полюсте қабылданған басқа А нүктесінің үдеуінен және осы полюстің айналасында фигураның айналуы кезінде М нүктесі алатын үдеуден тұрады. Модуль және үдеу бағыты тиісті параллелограммның құрылысы болып табылады 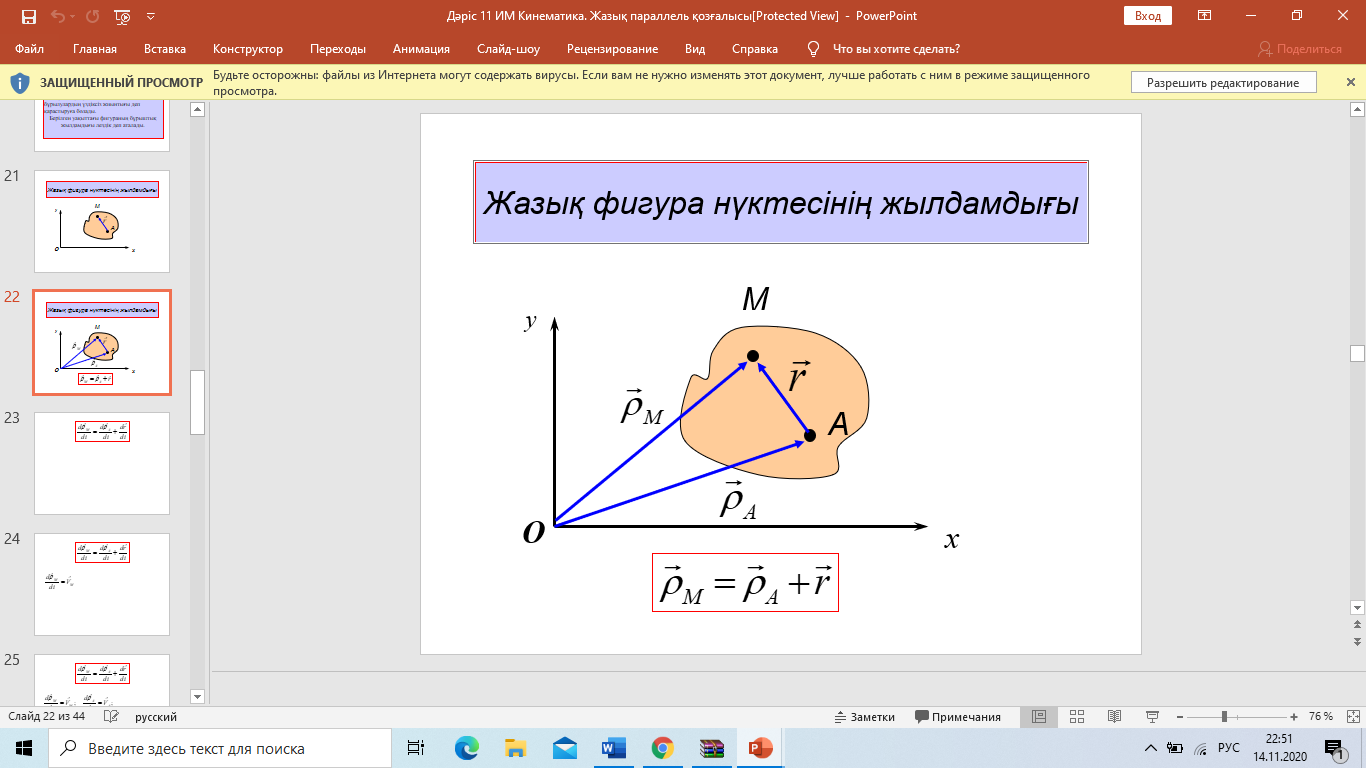 Жылдамдықтар проекциялары туралы теорема. Өзгермейтін кесінді ұштарының жылдамдықтарының кесінді бағытына проекциялары өзара тең 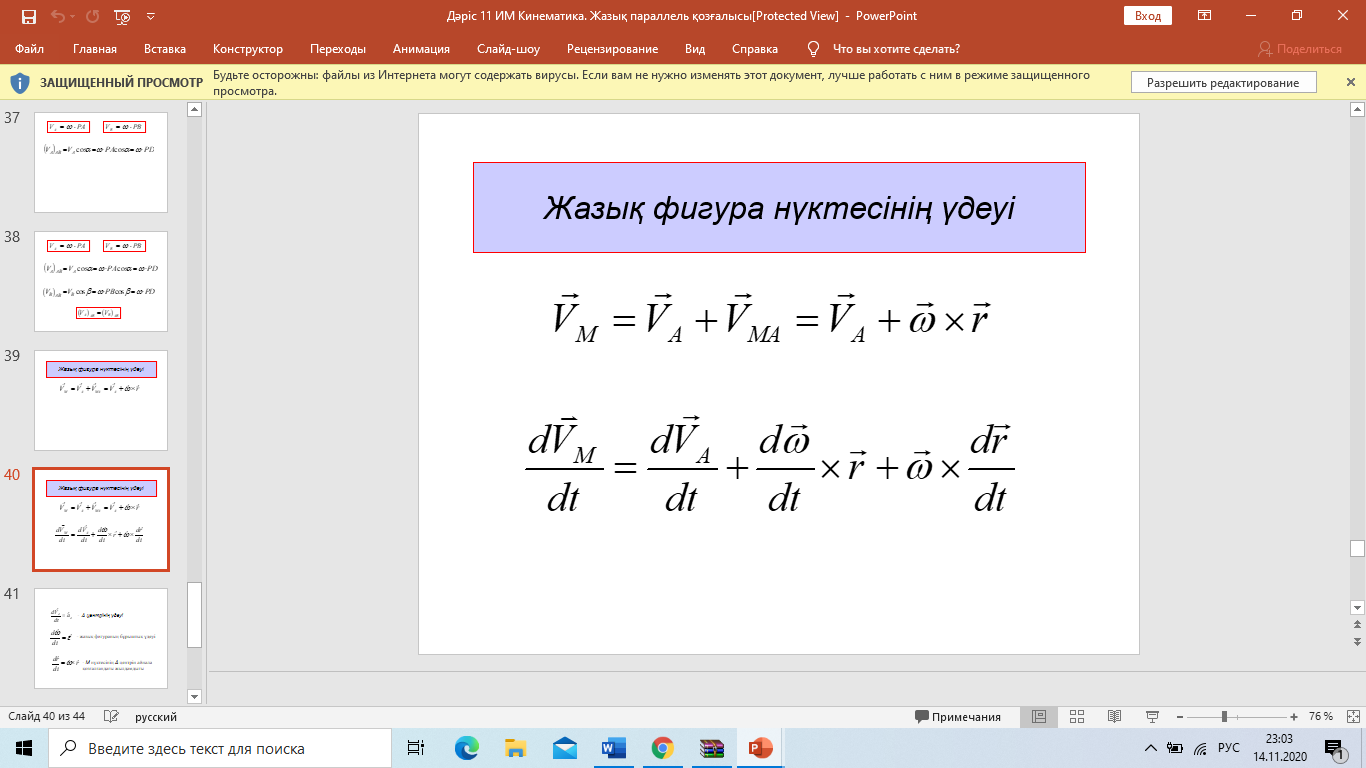 12.Жазық фигура нүктелерінің жылдамдықтарын лездік жылдамдықтар цетрі (ЛЖЦ) арқылы анықтау. ЛЖЦ орның анықтау тәсілдері. Жазық фигура нүктелері үдеулерін лездік үдеулер цетрі (ЛҮЦ) арқылы анықтау. Жазық фигураның кез-келген ілгерілемелі емес өз жазықтығындағы қозғалысын лездік айналу центрлеріне қатысты шексіз аз бұрылулардың үздіксіз жиынтығы деп қарастыруға болады.Берілген уақыттағы фигураның бұрыштық жылдамдығы лездік деп аталады. Дененің кез-келген нүктесінің жылдамдығын жылдамдықтың лездік центрімен анықтауға болады. Бұл жағдайда күрделі қозғалыс әртүрлі орталықтардың айналасында айналу тізбегі түрінде болады.Жылдамдықтың лехдік орталығы бұл жазықтықтағы нүкте оның абсолютті жылдамдығы қазірігі уақытта нөлге тең. 13.Абсолют қатты дененің құрама қозғалысы. Ілгерілемелі қозғалыстарды қосу. Дененің қиылысатын екі өстен айналмалы қозғалыстарын қосу. Қатты дененің аударма қозғалысы оның қозғалысы деп аталады, онда денемен қатты байланысқан кез-келген түзу бастапқы бағытына параллель қалады. Қатты дененің аудармалы қозғалысымен оның барлық нүктелері бірдей қозғалады. Дененің айналуын О нүктесінде қиылысатын бірнеше осьтердің айналасында қосқанда, дененің абсолютті қозғалысы О нүктесінен өтетін ОО1 осінің айналасында лезде айналады, ал бұл айналудың бұрыштық жылдамдығы бұрыштық жылдамдықтың құрамдас бөліктерінің геометриялық қосындысына тең болады. Жазық фигураның кез-келген өз жазықтығындағы орын ауыстыруын ілгерілемелі орын ауыстыру мен еркін таңдап алынған центрге (полюске) қатысты бұрылудан құруға болады. 14. Дененің өзара параллель екі өстен айналмалы қозғалыстарын қосу. Бірақ айналмалы қозғалыстарды қосқанда екі түрлі жағдай болуы мүмкін: бүктелген айналулардың лездік осьтері бір-бірімен қиылысады және қиылыспайды. Бірінші жағдайда, векторлардың қосындысы қарапайым қосу ережесімен анықталады ( бұрыштық жылдамдық векторы жылжымалы; оны Вектор сызығы бойымен тасымалдауға болады) және жаңа лездік ось бар. 15. Ілгерілемелі және айналмалы қозғалыстарды қосу. Бұрамалы қозғалыс. Ілгерілмелі-бұл қатты дененің қозғалысы, онда ондағы кез-келген сызық қозғалады, бастапқы бағытына параллель қалады. Абсолютті қатты дененің қозғалмайтын осьтің айналасындағы айналмалы қозғалысы-бұл айналу осі деп аталатын қозғалмайтын сызыққа перпендикуляр жазықтықта орналасқан дененің барлық нүктелерінің қозғалысы және орталықтары осы осьте орналасқан шеңберлердің сипаттамасы. Бұрандалы қозғалыс, V жылдамдығымен тік сызықты аударма қозғалысынан тұратын қатты дененің қозғалысы және V жылдамдығының бағытына параллель aa1 осінің айналасындағы бұрыштық жылдамдықпен айналмалы қозғалыс Динамика 1.Нукте динамикасының бірінші және екінші мәселелері. Динамика есептері екі негізгі түрде болуы мүмкін. Бұл мәселе еркін нүкте үшін төмендегідей: Динамиканың бірінші негізгі мәселесінде нүкте массасы және оның қозғалыс заңы берілген болып, қозғалтушы күшті табу сұралады. Ал, динамиканың екінші негізгі мәселесі нүкте массасы және оған әсер ететін күш белгілі болғанда, осы күш әсерінен алынатын кинематикалық элементтерді табудан тұрады. Нәтижеде материялық нүкте динамикасының негізгі теңдеуі төмендегідей жазылады:  Мұндағы - байланыс реакция күші. Демек, еріксіз нүкте динамикасының бірінші негізгі мәселесінде нүкте массасы және оның қозғалыс заңы және де осы нүктеге әсер ететін күш белгілі болғанда, реакция күші анықталады. Ал екінші мәселеде нүкте массасы және оған әсер ететін күш белгілі болғанда, нүктенің қозғалыс заңы мен реакция күшін анықтау керек. 2.Материялық нүкте қозғалысының декартті және табиғи өстеріне қатысты дифференциалдық теңдеулер. 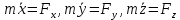 (2)Мұндағы 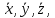 - нүкте үдеуінің осы координаттық остердегі проекциялары, Fx,Fy,Fz, нүктеге әсер етуші күштің осы остердегі проекциялары. (2) теідеулері материалдық нүкте қозғалысының декарттық координаттар остеріне қатысты алынған дифферинциалдық теңдеулері деп аталады.Еркін нүкте күшінің әсерінен қозғалыста болсын (14.4-сурет).Бұл жағдайда динамиканың негізгі теңдеуі (14.1) түрінде жазылады. (14.1) теңдеудегі үдеу векторын радиус - векторы арқылы өрнектейміз: 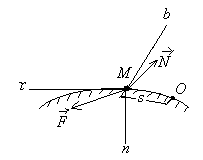 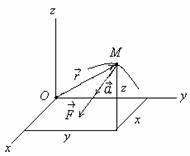. (14.7)   14.4 - сурет (14.7) - ні (14.1)-ге қойсақ, онда  (14.8) келіп шығады. (14.8) теңдеуі еркін нүкте қозғалысының дифференциал теңдеуінің векторлық өрнегі. (14.8) векторлық өрнектің Декарт координата өстеріндегі проекциялары төмендегідей болады:  (14.9) Бұл өрнектерде  арқылы күшінің координата өстеріндегі проекциялары белгіленген, x,y,z арқылы радиус- вектордың проекциялары, яғни М нүктенің координаттары. (14.9) теңдеулер, қисық сызықты қозғалыстағы нүкте қозғалысының дифференциал теңдеулері координат әдісімен берілген делінеді. Егер нүктенің қозғалыс бағыты мен күш бағыты бір түзу бойымен болса, нүкте қозғалысы түзу сызықты болады. Бұл жағдайда нүктенің қозғалыс бағыты үшін Ох өсін алсақ, оның диффренциал теңдеуі төмендегідей жазылады:  (14.10) Егер нүктенің қозғалысы жазықтықта болса, онда (14.9) теңдеулердің алғашқы екеуі (қозғалыс Охү жазықтығында) жазылады. (14.1) теңдеулердің табиғи координата өстеріндегі проекциялары төмендегідей болады (14.5-сурет): (  14.11) Кинематикадан бізге белгілі: =d /dt, 2 / , ab =0 (14.12) (14.12) өрнекті (14.11) теңдеулер жүйесіне апарып қойсақ, онда m  , Fn =m 2 / , Fb = 0 (14.13) келіп шығады. 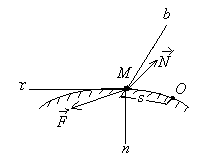 1 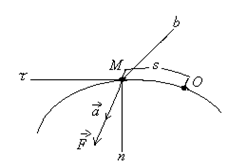 4.5 сурет 14.6 - сурет Нәтижеде табылған (14.13) теңдеур, нүкте қозғалысы табиғи әдіспен берілген кездегі оның дифференциал теңдеулері болып есептелінеді. Енді нүкте жылжымайтын жылтыр сызық үстінде қозғалып бара жатқан болсын (14.6-сурет). Санақ жүйесінің басын О деп, М нүктенің қисық сызықты координатасын деп қабылдаймыз. Қозғалмайтын жылтыр сызықтың нүктеге көрсететін әсерін реакция күшімен ауыстырып, нүктені байланыстан ойша босатамыз. Нәтижеде еріксіз нүкте динамикасының негізгі теңдеуі төмендегідей жазылады  , немесе  . (14.14) Бұл теңдеуді Декарт координат өстеріне проекцияласақ, еріксіз нүкте қозғалысының дифференциал теңдеулерінің координат тәсілдеріндегі өрнегі келіп шығады:  , , (14.15) (14.14) векторлық теңдеуді табиғи координат өстеріне проекциялаймыз. Онда  . Қозғалмайтын сызық тегіс болғандықтан реакция күшінің жанамаға болған проекциясы нөлге тең, яғни Демек,  (14.16) (14.16) материялық нүктенің қозғалмайтын жылтыр сызық үстіндегі қозғалысының дифференциал теңдеулерінің табиғи тәсілде өрнектелуі. Дербес жағдайда күші жанама жазықтықта орналасса, онда Ғb=0 болып нормал реакция күші траекторияның бас нормалымен бағыттас болады. 3.Еркін емес материялық нүктенің қозғалмайтын бет үстімен қозғалысының дифференциалдық теңдеулері. Егер нүктенің қозғалысы жазықтықта болса, онда (14.9) теңдеулердің алғашқы екеуі (қозғалыс Охү жазықтығында) жазылады. (14.1) теңдеулердің табиғи координата өстеріндегі проекциялары төмендегідей болады (14.5-сурет): ( 14.11) Кинематикадан бізге белгілі: =d /dt, 2 / , ab =0 (14.12) (14.12) өрнекті (14.11) теңдеулер жүйесіне апарып қойсақ, онда m , Fn =m 2 / , Fb = 0 (14.13) келіп шығады. 1 4.5 сурет 14.6 - сурет Нәтижеде табылған (14.13) теңдеур, нүкте қозғалысы табиғи әдіспен берілген кездегі оның дифференциал теңдеулері болып есептелінеді. |