Инж. инж мех (копия). Статика Бос жне бос емес дене. Байланыстар жне оларды реакциялары. Жиі кездесетін байлансытар трлері. Босату принципі
 Скачать 1.78 Mb. Скачать 1.78 Mb.
|
|
4.Еркін емес материялық нүктенің жылтыр қисық бойымен қозғалысының дифференциалдық теңдеулері. Енді нүкте жылжымайтын жылтыр сызық үстінде қозғалып бара жатқан болсын (14.6-сурет). Санақ жүйесінің басын О деп, М нүктенің қисық сызықты координатасын деп қабылдаймыз. Қозғалмайтын жылтыр сызықтың нүктеге көрсететін әсерін реакция күшімен ауыстырып, нүктені байланыстан ойша босатамыз. Нәтижеде еріксіз нүкте динамикасының негізгі теңдеуі төмендегідей жазылады Бұл теңдеуді Декарт координат өстеріне проекцияласақ, еріксіз нүкте қозғалысының дифференциал теңдеулерінің координат тәсілдеріндегі өрнегі келіп шығады: (14.14) векторлық теңдеуді табиғи координат өстеріне проекциялаймыз. Онда Қозғалмайтын сызық тегіс болғандықтан реакция күшінің жанамаға болған проекциясы нөлге тең, яғни Демек, (14.16) материялық нүктенің қозғалмайтын жылтыр сызық үстіндегі қозғалысының дифференциал теңдеулерінің табиғи тәсілде өрнектелуі. Дербес жағдайда күші жанама жазықтықта орналасса, онда Ғb=0 болып нормал реакция күші траекторияның бас нормалымен бағыттас болады. 5.Материалық нүкте үшін Даламбер принципі. Егер кез келген уацыт мезетінде механикалыц жүйенің әрбір нүктесінде, шын мәнісінде, әсер ететін сыртцы және ішкі күштерге цосымша, шартты түрде осы нүктелердің инерция күштерін түсірсек, онда осы алынган күштер жүйесі тепе-теңдікте болатын сияцты көрінеді. Осы түжырымды механикалық нүктелер жүйесі үшін Даламбер принципі деп айтуға болады. Механикалық жүйе үшін Даламбер принципін өрнектейтін теңдіктерінен күштер жүйесі тепе-теңдікте болады деп айтуға болмайды. Себебі жүйе нүктелерінің инерция күштері шын мәнісінде, нүктелерге емес, осы нүктелерді үдемелі қозғалысқа келтіретін денелер мен байланыс есебінде болатын басқа денелерге түсіріледі. Даламбер принципі қозғалыстың дифференциалдық теңдеулерін статикалық теңдеулер түрінде жазуға мүмкіндік береді.
Егер механикалық жиынға әсер ететін күштерді сыртқы күштер 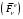 және ішкі күштер және ішкі күштер 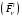 деп ажырататын болсақ, онда механикалық жиын үшін Даламбер принципі мынадай түрде жазылады: деп ажырататын болсақ, онда механикалық жиын үшін Даламбер принципі мынадай түрде жазылады: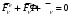 , , 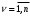 . .Инерция күші 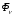 туралы әр түрлі көзқарастар көптеген ғылыми еңбектерде орын алған. Бұл күштерге байланысты туындайтын қорытынды: Даламбер принципі күштердің өзіндік санақ жүйесіндегі теңгерілу шартын береді. туралы әр түрлі көзқарастар көптеген ғылыми еңбектерде орын алған. Бұл күштерге байланысты туындайтын қорытынды: Даламбер принципі күштердің өзіндік санақ жүйесіндегі теңгерілу шартын береді.Даламбер принципін түрлендіру арқылы, қатты дененің тепе-теңдікте болуының шарттары төмендегідей түрлерде жазылады: 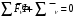 , ,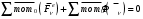 , ,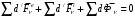 . .Бұл теңдеулер мағынасы жағынан динамиканың жалпы теоремаларының өрнектері болып табылады: 1) қозғалыс мөлшерінің өзгеруі туралы теорема өрнегі; 2) кинетикалық моменттің өзгеруі туралы теорема өрнегі; 3) кинетикалық энергияның өзгеруі туралы теорема өрнегі. 6.Материялық нүктенің салыстырмалы қозғалысының дифференциалдық теңдеулері. инерциялық сілтеме жүйесі бар 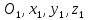 және материалдық нүкте m, қолданылатын күштер әрекет етеді және материалдық нүкте m, қолданылатын күштер әрекет етеді 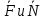 . . 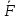 - белсенді күштердің нәтижесі - белсенді күштердің нәтижесі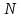 - байланыс реакцияларының әсер етуші күштері - байланыс реакцияларының әсер етуші күштеріЕгер 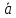 - жеделдету нүктесі салыстырмалы инерциялық санақ жүйесіне (абсолюттік жеделдету), онда теңдеуі нүкте қозғалысының векторлық нысан иеміз - жеделдету нүктесі салыстырмалы инерциялық санақ жүйесіне (абсолюттік жеделдету), онда теңдеуі нүкте қозғалысының векторлық нысан иеміз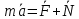 Егер сіз басқа инерциялық емес сілтеме жүйесін енгізсеңіз Oxyz жалпы жағдайда еркін қатты дене ретінде инерциалды түрде қозғалуы мүмкін, онда үдеулерді қосу теоремасы бойынша бізде 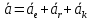 Мұндағы 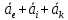 тиісінше, портативті, салыстырмалы және Кориолис үдеуі. тиісінше, портативті, салыстырмалы және Кориолис үдеуі.Терминдерді ауыстырғаннан кейін абсолютті үдеудің мәнін алмастыра отырып, сол жақтан оңға қарай 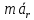 басқа, біз басқа, біз 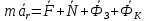 аламыз. аламыз.Мүндағы 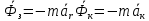 тиісінше портативті және Кориолис Инерция күштері деп аталады. Кориолистің динамикалық теоремасы немесе нүктенің векторлық формадағы салыстырмалы қозғалысының теңдеуі алынды: материалдық нүкте инерциялық емес эталондық жүйеге қатысты инерциялық емес шеңбермен бірдей қозғалады, тек қолданылатын белсенді күштер мен байланыс реакцияларына портативті және Кориолис Инерция күштерін қосу керек. тиісінше портативті және Кориолис Инерция күштері деп аталады. Кориолистің динамикалық теоремасы немесе нүктенің векторлық формадағы салыстырмалы қозғалысының теңдеуі алынды: материалдық нүкте инерциялық емес эталондық жүйеге қатысты инерциялық емес шеңбермен бірдей қозғалады, тек қолданылатын белсенді күштер мен байланыс реакцияларына портативті және Кориолис Инерция күштерін қосу керек.координаталардың жылжымалы осіне проекцияларда : 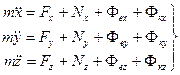 Бұл декарттық қозғалмалы координаталар осіндегі проекциялардағы қозғалмалы координаттар жүйесіне қатысты нүкте қозғалысының дифференциалдық теңдеулері. Олар инерциялық тірек шеңберіне қатысты абсолютті қозғалыстың дифференциалдық теңдеулерінен тек анықтамалық жүйенің инерциялық емес түзетулерінің болуымен ерекшеленеді. 7 Материялық нүктенің еркін тербелісінің дифференциалдық теңдеуі. Дифференциальное уравнение свободных колебаний материальной точки. Қандай да бір дәрежеде қайталанып тұратын қозғалыстар тербелістер деп аталады. Жүйені тепе-теңдік күйден шығарғаннан кейін өздігінен өтетін тербелістереркінтербелістердеп аталады. Еркін тербелістердің дифференциалдық теңдеуі: Х+k2x=0, мұндағы k2=c/m,k-қатаңдық коэффициент(рад/с), m- массасы(кг). Бұл дифференциалдық теңдеудің жалпы шешімі: х=C1sinkt+C2coskt, мұндағы С1 және С2-тұрақты интегралдар 8 Материялық нүктенің өшетін тербелісіндегі дифференциалдық теңдеуі. Апериодты қозғалысы. Дифференциальное уравнение затухающих колебаний материальной точки. Апериодическое движение Нақты жағдайда тербелістегі денеге кедергі күштердің әсерінен амплитуданың шамасы азайып, тербеліс бірте-бірте өше бастайды. Ал кедергі күшінің шамасы жылдамдыққа тура пропорционал, сонда Fk=-rv,мұндағы r-кедергі коэффициенті, минус таңбасы кедергі күшінің қозғалыс бағытына қарама-қарсы екендігін көрсетеді. Енді тербеліс теңдеуін Ньютонның екінші заңы бойынша жазайық: ma=F+Fk , мұндағы m-тербелістегі дененің массасы, а-оның үдеуі, F-қайтарушы күш, ол сан жағынан F=-kx, мұндағы k -серпімділік коэффициенті. Тербелістегі дененің жылдамдығы мен үдеуі Осы формула өшетін тербелістің дифференциал түрдегі теңдеуі деп аталады. Апериодты қозғалыс – тербелмелі жүйенің үлкен кедергілі ортадағы қозғалысы. Апериодтық қозғалыс R ортасының кедергі коэффициентінің жоғарылауымен және, сәйкесінше, сөну коэффициентінің жоғарылауымен β өшу тербелістерінің периоды  өседі. өседі. 9 Материялық нүктенің кедергісіз ортадағы еріксіз тербелісінің дифференциалдық теңдеуі. Резонанс Дифференциальное уравнение вынужденных колебаний материальной точки при отсутствии силы сопротивления среды. Резонанс. Сыртқы периодты күштің әсерінен жүйеде пайда болатын тербелістер еріксіз тербелістер деп аталады. 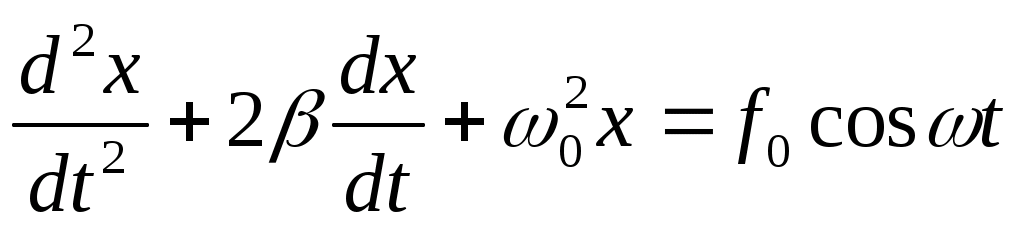 еріксіз тербелісінің дифференциалдық теңдеуі. еріксіз тербелісінің дифференциалдық теңдеуі.Еріксіз тербелістің амплитудасын жазатын болсақ,  , ( 7.15) , ( 7.15)ал бастапқы фазасының өрнегі келесі түрде жазылады: Осы формуладан w®w0 онда еріксіз тербелістің амплитудасы өседі. Егер b=0, яғни кедергі күш жоқ болса, w=w0 болып Amax артып, шексіз өседі. Сөйтіп еріксіз тербеліс кезінде w=w0 болады, амплитуданың артуы резонанс құбылысы деп аталады. Резонанс (лат. resono, фр. resonance — үн қосу, дыбыс қайтару) — периодты түрде сырттан әсер етуші күштің жиілігі тербелмелі жүйенің меншікті жиілігіне жақындағанда сол тербелмелі жүйедегі еріксіз тербелістер амплитудасының күрт арту құбылысы; мәжбүр етуші күштің жиілігі жүйе тербелісінің меншікті жиілігіне жуықтаған кезде жүйедегі мәжбүр тербеліс амплитудасының кенеттен артып кету кұбылысы. 10 Материялық нүктенің кедергілі ортадағы еріксіз тербелісіндегі дифференциалдық теңдеуінің жалпы шешуі. Общее решение дифференциального уравнения затухающих колебаний материальной точки. Еріксіз тербеліс теңдеуі нақты тербеліс жүйелерінің қозғалысын сипаттайды. Дифференциалды түрде ол келесідей жазылады: 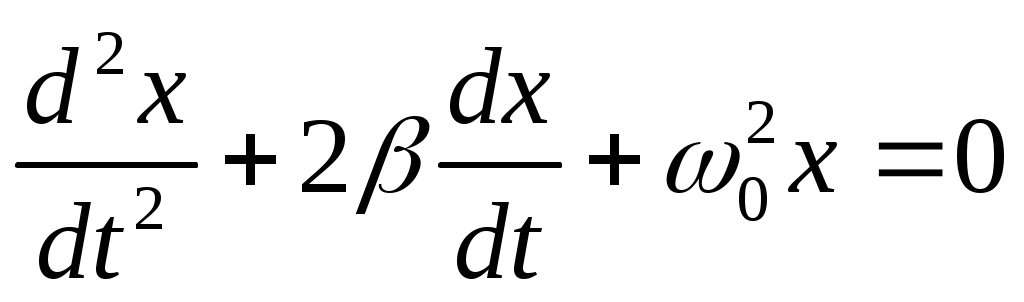 . .Ал оның жалпы шешуі былай болады: у=А(t)cos( 11 Материялық нүктенің қозгалыс мөлшері. Күш импульсі. Материялық нүктенің қозгалыс мөлшерінің өзгеруі туралы теорема. Количество движения материальной точки. Импульс силы. Теорема об изменении количества движения материальной точки. Материалық Нүктенің қозғалыс мөлшері деп нүктенің массасы мен оның жылдамдығының көбейтіндісіне тең шаманы айтады. векторы нүктенің траекториясына жанама бағытталады. Күштің импульсі деп күштің элементар уақыт аралығына көбейтіндісін атайды (5.13) Импульс күштің әсер ету сызығы бойымен бағытталады. күшінің шекті t1 уақыт ішіндегі импульсі . (5.14) Импульстің модулі мен бағытын оның проекциялары арқылы табуға болады  Динамиканың негізгі теңдеуін келесі түрде жазуға болады  . (5.16) . (5.16)Бұл дифференциалдық түрдегі нүктенің қозғалыс мөлшерінің өзгеруі туралы теоремасы: нүктенің қозғалыс мөлшерінің уақыт бойынша туындысы нүктеге түсетін күштердің векторлық қосындысына тең. Шекті түрдегі сол теорема: нүктенің қозғалыс мөлшерінің кейбір уақыт аралығында өзгеруі оған түсетін күштердің сол уақыт аралықтағы импульстерінің векторлық қосындысына тең . 12 Материялық нүкте қозгалыс мөлшері моментінің өзгеруі туралы теорема. Теорема об изменении момента количества движения материальной точки Нүктенің қозғалыс мөлшерінің кейбір О центріне қатысты моменті деп келесі теңдікпен анықталатын векторлық шамасын айтады (5.18) мұндағы - қозғалыстағы нүктенің О центрінен жүргізілген радиус-векторы. Сонда векторы және О центрі арқылы өтетін жазықтыққа перпендикуляр бағытталады, aл модулі . Нүктенің қозғалыс мөлшерінің О центрінен өтетін Оz өсіне қатысты моменті векторының сол өске проекциясына тең  мұндағы g - векторы мен Оz өсі арасындағы бұрыш. Теорема: нүктенің қозғалыс мөлшерінің кейбір қозғалмайтын центрге қатысты алынған моментінің уақыт бойынша туындысы әсер ететін күштің сол центрге қатысты моментіне тең  . (5.20) . (5.20)Өске қатысты моменттер теоремасы . (5.21) (5.20) теңдеуінен болса, болатыны шығады. 13.Күштің жұмысы. Күш қуаты dt элементар уақыт аралығы арқылы күштің W қуатының көбейтіндісіне тең dA скаляр шамасы деп аталады. Егер V = dr / dt екенін ескерсек, онда (19.7) теңдіктен аламыз. мұндағы y - күш қолданылатын векторлар арасындағы бұрыш және оны қолдану нүктесінің элементар ығысуы; dr = xds. Күш жұмысы күштің скаляр көбейтіндісіне және оны қолдану нүктесінің элементар қозғалысына тең. Күш қуаты дегеніміз - күштің әсер ету нүктесінің жылдамдық векторына күш векторының скаляр көбейтіндісіне тең алгебралық шама: 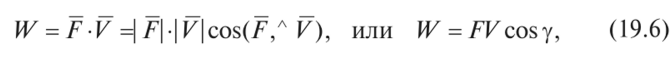 Мұндағы y - F және V векторлары арасындағы бұрыш. Күш күшінің белгісі F және V векторларының өзара бағытталуын сипаттайтын cos y мәнін береді, егер y бұрышы өткір болса, онда қуат оң болады (кейінірек көрсетілгендей, бұл жағдайда күштің әрекеті оны қолдану нүктесінің жылдамдығын арттырады). Егер бұрыш доғал болса, онда қуат теріс болады (күштің әсерінен жылдамдық азаяды). Егер бұрыш түзу болса, онда күштің күші нөлге тең болады (мұндай эффектпен күш оны қолдану нүктесінің жылдамдығының модулін өзгертпейді). 14.Материалдық нүктенің кинетикалық энергиясының өзгеруі туралы теорема. Материалдық нүктенің оның кейбір ығысу кезіндегі кинетикалық энергиясының өзгерісі бірдей ығысу кезінде нүктеге әсер ететін барлық күштердің роботының алгебралық қосындысына тең. 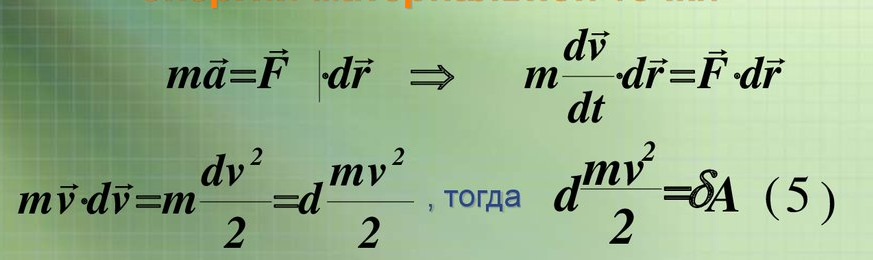 |

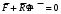
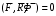
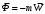
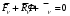 ,
,