Инж. инж мех (копия). Статика Бос жне бос емес дене. Байланыстар жне оларды реакциялары. Жиі кездесетін байлансытар трлері. Босату принципі

• Название: Статика Бос жне бос емес дене. Байланыстар жне оларды реакциялары. Жиі кездесетін байлансытар трлері. Босату принципі
• Дата: 02.06.2021
• Размер: 1.78 Mb.
• Имя файла: инж мех (копия).docx
• Тип: Документы; #213268
• страница: 5 из 5

15.Механикалық жүйенің массаларының центрі

Механикалық жүйенің масса центрі радиус векторы болатын С геометриялық нүктесі ретінде алынады.

rC = ΣmCi rCi / m,

мұндағы m - механикалық жүйенің массасы.

Механикалық жүйенің массасы m формуламен анықталады

m = CmCi

Механикалық жүйенің масса центрі - осы нүктеден шыққан радиус векторлары арқылы механикалық жүйе құратын барлық материалдық нүктелер массаларының көбейтінділерінің қосындысы болатын геометриялық нүкте.

16. Механикалық жүйенің инерция моменті\

(«инерцияның осьтік моменті») - бұл жүйенің барлық n материалды нүктелерінің массаларының олардың осіне дейінгі арақашықтықтарының квадраттары бойынша көбейтінділерінің қосындысына тең Ja физикалық шамасы: мұндағы: i-ші нүктенің массасы, i-ден қашықтық,-оське дейінгі нүкте.

Материалдық нүктенің инерция моменті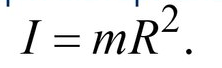



Материалдық нүктелер жүйесінің инерция моменті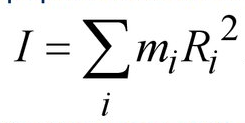



Қатты дененің инерция моменті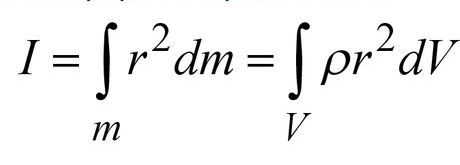



Инерция радиусы –– көмегімен берілген оське қатысты дене инерция моменті дене массасының осы шама квадратына көбейтіндісімен өрнектелетін ұзындық өлшемді шама.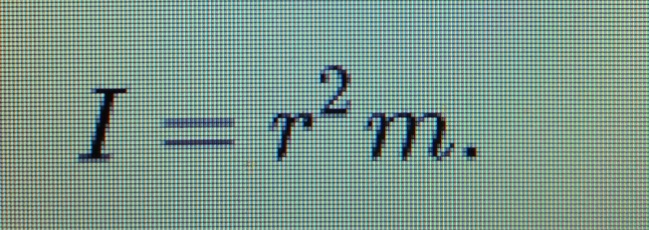

{\displaystyle I=r^{2}m.}

17. Дененің параллель өстерге қатысты инерция моменттері. Гюйгенс-Штейнер теоремасы.



Гюйгенс - Штайнер теоремасы. Қатты дененің кез-келген оське қатысты инерция моменті дененің массасына, формасы мен өлшеміне, сондай-ақ дененің осы оське қатысты орнына байланысты.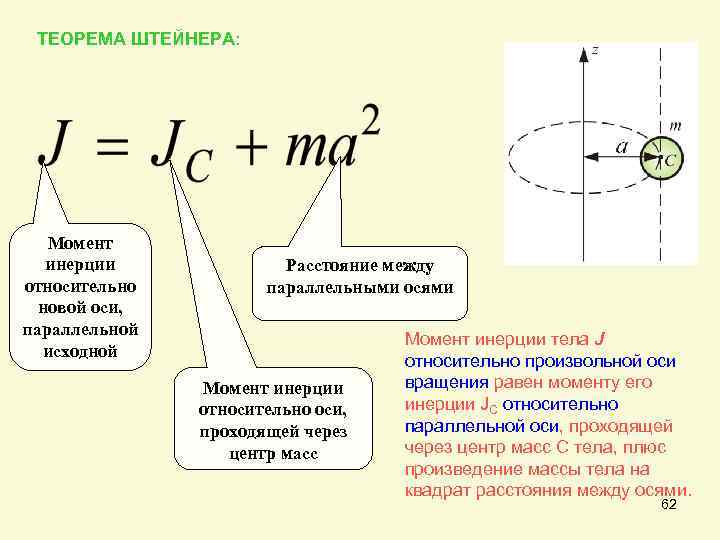



18. Механикалық жүйе қозғалысының дифференциалдық теңдеулері.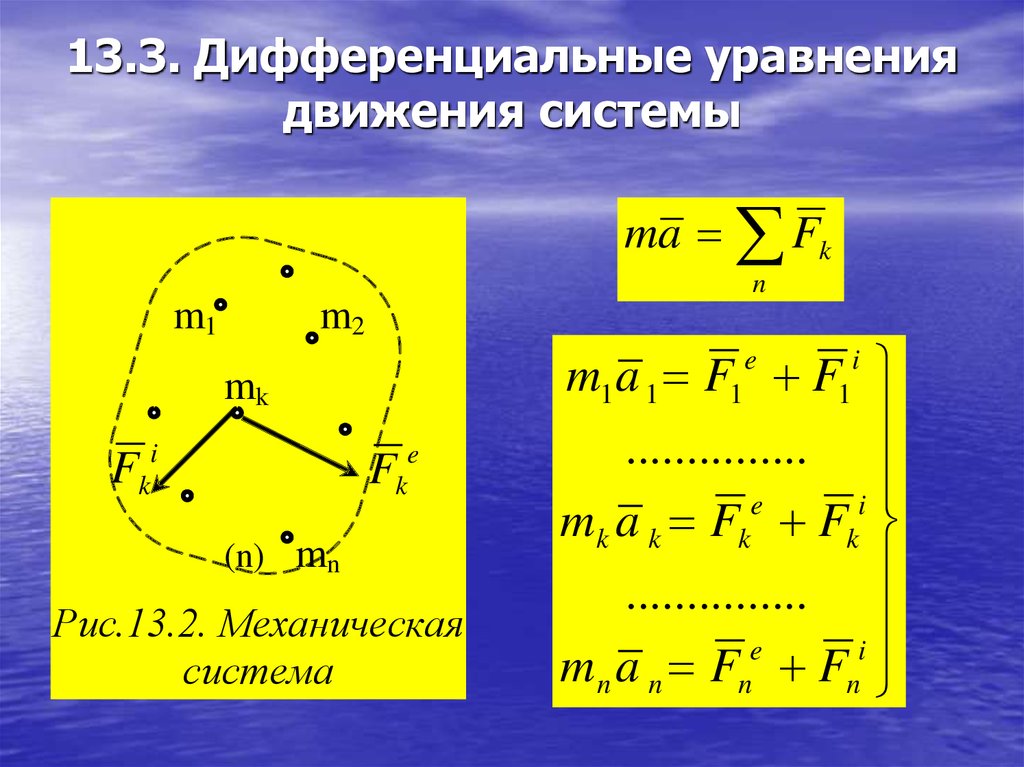




19.Механикалық жүйенің массалар центірінің қозғалысы туралы теорема.

Жүйенің масса центрінің (инерция центрі) қозғалысы туралы теорема Ньютон заңдары бойынша жүретін динамиканың жалпы теоремаларының бірі болып табылады. Механикалық жүйенің масса центрінің үдеуі дененің жүйесіне әсер ететін ішкі күштерге тәуелді емес екенін растайды және осы үдеуді жүйеге әсер ететін сыртқы күштермен байланыстырады.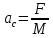



Бұл теңдеу масса центрінің қозғалыс заңының жазбасы болып табылады. Жүйенің масса центрінің қозғалысы жүйеге әсер ететін барлық сыртқы күштер қолданылатын бүкіл жүйемен бірдей массаның материалдық нүктесінің қозғалысымен бірдей.Басқаша айтқанда, жүйенің масса центрі мен жүйенің өз массасының үдеуінің көбейтіндісі осы жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысына тең болады.

20. Механикалық жүйенің қозғалыс мөлшері. Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема.

Механикалық жүйенің қозғалыс (импульс) шамасы жүйеге кіретін барлық денелердің қозғалыс (импульс) мөлшеріне тең мән деп аталады. Дене жүйелеріне әсер ететін сыртқы күштердің импульсі дегеніміз - дене жүйелеріне әсер ететін барлық сыртқы күштердің импульстарының қосындысы.

Жүйенің қозғалыс (импульс) мөлшерінің өзгеруі туралы теорема динамиканың жалпы теоремаларының бірі, ол Ньютон заңдарының салдары болып табылады. Импульсті жүйені құрайтын денелерге әсер ететін сыртқы күштердің импульсімен байланыстырады.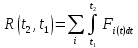



21. Механикалық жүенің нүктеге және өске қатысты кинетикалық моменті.

О центріне қатысты механикалық жүйенің кинетикалық моменті механикалық жүйеге кіретін барлық материалдық нүктелердің қозғалыс мөлшерінің моменттерінің геометриялық қосындысына (негізгі момент) тең вектор деп аталады:

 .

Механикалық жүйенің белгілі бір оське қатысты кинетикалық моменті-механикалық жүйенің осы оське қатысты барлық материалдық нүктелерінің қозғалыс моменттерінің алгебралық қосындысы. Нүктенің қозғалыс мөлшерінің моменті де (кез – келген оське қатысты жүйенің кинетикалық моменті де сол оське   кинетикалық моментінің проекциясы болып табылады. Мысалы, механикалық жүйенің z осіне қатысты кинетикалық моменті:

 .

Ерекше маңызды жағдай. Тұрақты айналу осіне қатысты қатты дененің кинетикалық моменті:  

• 
  - бұрыштық жылдамдық
  

- дененің айналу осіне қатысты инерция моменті.

22. Механикалық жүйенің кинетикалық моментінің өзгеруі туралы теорема.

Моменттердің кинетикалық жүйесінің өзгеруі туралы теорема (жүйенің импульс моментінің өзгеруі туралы теорема) - Ньютон заңдарынан кейінгі динамиканың жалпы теоремаларының бірі. Бұрыштық импульстің өзгеруі денеге әсер ететін жүйені құрайтын сыртқы күштердің моментімен байланысты. Кез-келген денеден тұратын кез-келген механикалық жүйе теоремада айтылған жүйе ретінде әрекет ете алады.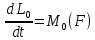



23. Механикалық жүйенің кинетикалық энергиясы (ілгермелі жазық параллель қозғалыстағы).

Кинетикалық энергия - бұл қарастырылатын механикалық жүйені құрайтын материалдық нүктелердің қозғалысының өлшемі болып табылатын және тек осы нүктелердің массасы мен жылдамдық модуліне тәуелді скаляр функция.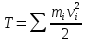

1. 
   Параллель қозғалыс - бұл қозғалыста кинетикалық энергия сатылы және айналмалы қозғалыстар энергиясынан жинақталады.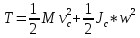
   

2. 
   Ілгермелі жазыққозғалыс - денеге байланысты кез-келген түзу бастапқы қалпына параллель болып қалатын және сол уақытта қатты дененің барлық нүктелері бірдей уақыт аралығында бірдей орын ауыстыруды орындайтын қатты дененің қозғалысы.
   

24. Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема.

Жүйенің кинетикалық энергиясының өзгеруі оның кейбір соңғы ығысуымен, жүйеге қолданылатын барлық сыртқы және ішкі күштердің орын ауыстыруындағы жұмыс қосындысына тең болады.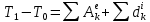



Кинетикалық энергияның интегралдық түрдегі теоремасы былай айтылады: Механикалық жүйенің бір орналасу жағдайынан екінші бір орналасу жағдайына көшу кезінде жасаған орын ауыстыруындағы кинетикалық энергиясының өзгеруі жүйеге әсер етуші барлық сыртқы және ішкі күштердің сол орын ауыстыруындағы жұмыстарының қосындысына тең болады.

Аналитикалық механика элементтері

1. 
   Потенциалдық энергия. Механикалық энергияның сақталузаны
   

А) Энергия - дененің жұмыс істеу қабілеті немесе жұмыс қоры. Дененің Жердің центрінен арақашықтығын арттыру үшін (денені көтеру үшін) онымен жұмыс жасау керек. Ауырлық күшіне қарсы жұмыс денеде потенциалды энергия ретінде жинақталады.

Егер:

Эп - дененің потенциалдық энергиясы, позиция энергиясы (Джоуль)

м - дене массасы(кг)

h - денені көтеретін биіктік (метр)

g - ауырлық күшінің үдеуі 9.81 (м / с2)

Дененің потенциалдық энергиясы:



Биіктікте орналасудың потенциалдық энергиясы.

Формула (1) бүкіл гравитациялық биіктікте гравитациялық үдеу тұрақты болған жағдайда дұрыс, яғни. салыстырмалы түрде төмен биіктікке көтерілген жағдайда. Кез-келген аспан денесінің гравитациялық өрісінде ауырлық күші және сәйкесінше дененің еркін түсу үдеуі осы дененің центрінен қашықтық квадратына пропорционалды түрде азаяды. Сондықтан үлкен биіктікке көтерілгенде g = g (h) және, демек, F = F (h) екенін ескеру қажет: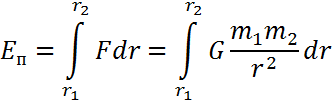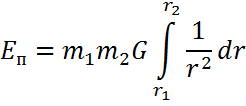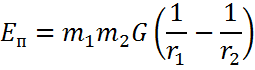







Мұнда:

En (A) - гравитациялық күшке қарсы жұмыс (Джоуль)

F - екі дене бір-біріне тартылатын тартылыс күші (Ньютон)

m1 - бірінші дененің массасы (кг)

м2 - екінші дененің массасы (кг)

r - денелер массаларының орталықтары арасындағы қашықтық (метр)

r1 - денелердің масса орталықтары арасындағы бастапқы арақашықтық (метр)

r2 - денелер массаларының орталықтары арасындағы соңғы арақашықтық (метр)

G - гравитациялық тұрақты 6,67 10-11 (м3 / (кг s2))

В) Механикалық энергияның сақталу заңы

Бұл заңда энергия із-түзсіз жоғалып кете алмайды немесе жоқтан пайда болмайды дейді.

Жабық жүйенің өз энергиясынан бас тартпайтын және сырттан энергия алмайтын жалпы энергиясы өзгеріссіз қалады.

Механикада қолданылатын бұл жалпы заң мынаны білдіреді:

Тұйық механикалық жүйеде энергияның механикалық түрлерінің қосындысы (айналмалы қозғалыс энергиясын қосқандағы потенциалдық және кинетикалық энергия) өзгеріссіз қалады.

2. 
   Байланыстар және және олардын классификациясы. Ықтималды орын ауыстыру принципі. Күштің виртуалды жұмысы. Идеал байланыстар
   

А) Механикалық жүйенің нүктелеріне қойылатын аналитикалық байланыстар байланыс теңдеулері түрінде көрсетіледі, ол ең жақсы жағдайда нүктелердің координаттарын, олардың жылдамдықтары мен уақытын қамтуы мүмкін

f(x₁,y₁,z₁…; x_n,y_n,z_{n .}... ; x₁(сверху точка),y₁(сверху точка),z₁(с.т)…; x_n,y_n,z_n (сверху точка) t)=0

Байланыстың түрлері:

1. 
   Геометриялық және кинематикалық
   
2. 
   Стационарлық және стационарлық енмес
   
3. 
   Холономикалық және холономикалық емес
   
4. 
   Ұстамды және ұстамсыз
   

Геометриялық байланыстар дегеніміз - теңдеулеріне тек жүйенің нүктелерінің координаталары ғана кіреді және уақыт болуы мүмкін.

Кинематикалық байланыстар дегеніміз - жүйенің нүктелерінің координаттарынан басқа, осы координаттардың уақытқа және, мүмкін, уақытқа қатысты алғашқы туындыларын қамтитын теңдеулері. Кинематикалық байланыстар интегралданатын және интегралданбайтын болуы мүмкін.

Уақыт нақты енбейтін теңдеулердегі байланыстар стационарлық деп аталады. Егер уақыт шектеу теңдеулеріне нақты енгізілсе, онда шектеу стационар емес болады.

Холономикалық геометриялық және интегралданатын кинематикалық шектеулерді қамтиды.

Теңдеуі интеграцияланбайтын кинематикалық байланыс холономикалық емес байланыс деп аталады.

Б) Dt уақытында орындалған қолданылатын күштердің әсерінен нүктенің шексіз аз орын ауыстыруы нақты орын ауыстыру деп аталады және dr (жоғарыдан вектор) арқылы белгіленеді.

нүктенің мүмкін орын ауыстыруын нүктеге қойылған шектеулер уақыттың қарастырылған сәтінде рұқсат етілген шексіз аз орын ауыстыру деп атайды.

M dr(вектор)

r(в) dr

жүйенің мүмкін орын ауыстыруын жүйе нүктелерінің кез-келген ықтимал орын ауыстыруларының жиынтығы деп атайды.Ықтималды орын ауыстыру принципі: Материалдық жүйенің идеалды және стационарлық байланыстары бар тепе-теңдігінде жүйенің тепе-теңдік күйінен кез-келген ықтимал ығысуына берілген барлық күштердің жұмысының қосындысы нөлге тең болады.

Әрине, егер жүйеде жетілмеген байланыстар болса, мысалы, үйкеліспен немесе серіппелі сияқты болса, онда бұл байланыстардың реакцияларының мүмкін жұмысы жұмыс теңдеуіне қосылуы керек.Ықтимал орын ауыстыру принципін басқа формада жазуға болады.Егер мүмкін жылдамдықтардың көмегімен нүктелердің мүмкін орын ауыстырулары анықталса : мұндағы уақыт ерікті шексіз шама болса, онда (1) жұмыстардың теңдеуі келесідей жазылады 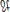және оны бөлгенде аламыз

• 
  -күштердің бағыттары мен векторларының бағыттары арасындағы бұрыштар қай жерде күштердің мүмкін болатын жылдамдықтарының күштері.
  

C) күштің оны қолдану нүктесінің ықтимал жылжуларының біріне жұмыс істеуі күштің ВИРТУАЛДЫ жұмысы деп аталады

ⅆA=Fdr=F_Xdx+F_Ydy+F_zdz

D) Идеал байланыстар деп жүйенің нүктелерінің кез-келген ықтимал ығысуындағы реакциялардың қарапайым жұмысының қосындысы нөлге тең болатын қосылыстарды айтады. Үйкеліссіз барлық стационарлық геометриялық байланыстар идеалды байланыстар болып саналады.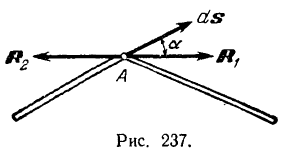

Егер қосылыс екі денені жалғайтын жылжымалы топса болса (237-сурет), онда бұл денелердің бір-біріне реакциясы шамасы бойынша тең және бір түзу бойымен қарама-қарсы бағытта бағытталған

3. 
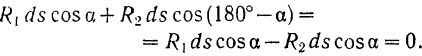   Жалпыланған координаттар мен жылдамдықтар. Жалпыланған күштер
   

Бір-біріне тәуелсіз параметрлер жалпыланған координаталар деп аталады.q әрпімен белгіленеді.

Бұл теңдеулер жалпыланған координаталардағы жүйенің қозғалыс теңдеулері деп аталады.Егер уақытқа қатысты жалпыланған координаталардың туындыларын алсақ, онда жалпыланған жылдамдықтар алынады:

Жалпыланған жылдамдықтың өлшемі жалпыланған координатаның өлшеміне байланысты:

q - сызықтық шама, - сызық жылдамдығы

q - бұрыш, -бұрыштық жылдамдық

q-аудан, -сектор жылдамдығы

Жалпыланған күш - виртуалды жұмыс үшін өрнек мерзіміндегі жалпыланған координатаның өзгеруіне арналған коэффициент мәні

• 
  -жалпыланған күш
  

4. 
   Механикалық жүйенің жалпыланған координаталардағы тепе-теңдік шарттары.
   

механикалық жүйенің тепе-теңдігі үшін жүйе үшін таңдалған жалпыланған координаттарға сәйкес келетін барлық жалпыланған күштердің нөлге тең болуы қажет және жеткілікті. Q1dq₁+Q2dq₂+…+Q_ndq_n

Тепе-теңдік шарттарының саны жалпыланған координаттар санына тең, яғни координаталардың еркіндік дәрежелерінің саны: Q1=0,Q2=0…Qn=0

5. 
   Механиканың жалпы теңдеуі - бұл динамика мен статика есептерін шешудің жалпы әдісін беретін және теориялық механиканың негізгі қағидаларының бірі болып табылатын Д'Альберт-Лагранж принципінің математикалық тұжырымдамасы.Бұл принцип ықтимал ығысу принципі мен Даламбер принципін біріктіреді.
   

Динамиканың жалпы теңдеуі: немесе

6. 
   Механикалық жүйенің жалпыланған координаталардағы дифференциалдық теңдеулері. Лагранждың екінші тектегі теңдеулері
   

Екінші типтегі Лагранж теңдеулері - механикалық жүйенің қозғалыс дифференциалдық теңдеулері, бұл Лагранж формализмінің көмегімен алынған.

Екінші типтегі Лагранж теңдеулері формада болады

мұндағы i = 1, 2,… n (n - механикалық жүйенің еркіндік дәрежесінің саны). Лагранж - жүйенің кинетикалық және потенциалдық энергиялары арасындағы айырмашылық.

Потенциалды және потенциалды емес болған кезде (жалпыланған күштер, оң жағы пайда болады:

Потенциалды емес күштерге, мысалы, үйкеліс күші жатады. Бұл жағдайда екінші түрдегі Лагранж теңдеулерін сәл өзгеше түрде қайта жазуға болады:



 {\displaystyle T(q_{i},{\dot {q}}_{i},t)} -жүйенің кинетикалық энергиясы, - жалпыланған күш

Механикалық жүйенің жалпыланған координаттары деп аталады

q1, q2, ..., qk параметрлері, олардың көмегімен бір-біріне тәуелді емес

сіз кез-келген сәтте осы жүйенің орналасуын және

ол арқылы декарттық координаттарды көрсетуге болады

оның барлық тармақтары.

Тәуелсіз жалпыланған координаталардың k саны градус санына тең

осы жүйенің еркіндігі. Екінші типтегі Лагранж теңдеулері - жүйе

екінші ретті қарапайым дифференциалдық теңдеулер

q1, q2, ..., qk, белгісіз жалпыланған координаттарына қатысты

идеалға бағынышты механикалық жүйенің қозғалысын сипаттайтын

байланыстар.