Стат анализ 40 вариант. стат анализ 40 вариант. Статистический анализ и планирование эксперимента макет отчета по контрольной работе для обучающихся по заочно форме обучения
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
1 2 Цель работы. Освоить компетенции выполнения статистического анализа двумерных данных, выявить зависимость (связь) между случайными величинами.2.1.1 Исходные данные В качестве исходных данных принято двух последовательных случайных величин: первая – Коэффициент пористости, m; вторая - Водонасыщенность на фронте,Sф%. Исходные данные представлены в таблице 2.1. Таблица 2.1 – Исходные данные
Примем: в качестве аргумента Xi - Коэффициент пористости, m;; в качестве функции Yi - Водонасыщенность на фронте,Sф%.. Взаимосвязь между двумя случайными величинами может быть оценена следующими методами: Визуальный метод Корреляционный анализ Регрессионный анализ Визуальный анализ Визуальный метод –изучении зависимости между двумя переменными. По данным таблицы 2.1 построен точечный график (рис. 2.1).  Рисунок 2.1 – Точечный график Вывод: по точечной диаграмме визуально невозможно установить характер связи между заданными последовательностями случайных величин, поэтому необходимо выполнить корреляционный анализ. Корреляционный анализ Корреляционная зависимость – является распространенной общей характеристикой двумерных данных в том же смысле, в каком среднее и стандартное отклонение являются важными характеристиками для анализа одномерного набора данных. Корреляционный анализ выполнен с помощью пакета «Анализ данных» программы Excel, результаты которого показаны в таблице 2.2. Таблица 2.2 - Результаты корреляционного анализа
Вывод: связь между значениями сильная. Характер связи положительный. Регрессионный анализ Регрессионный анализ – определяет форму (вид) связи между этими переменными. Используется для прогнозирования одной переменной на основании другой (как правило, Y на основании X), или показывает, как можно управлять одной переменной с помощью другой. Регрессионный анализ заданных последовательностей выполнен с помощью режима Регрессия пакета «Анализ данных» программы MS Excel. Сгенерируются результаты по регрессионной статистике, представленные в таблице 2.3. Таблица 2.3- Результаты регрессионного анализа
Рассчитанные в таблицах характеристики представляют собой: Стандартная ошибка регрессии (Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Регрессия (лат. regressio — обратное движение) в статистике — статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин; введена Фрэнсисом Гальтоном (1886) R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям. Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации. Построение регрессионных моделей выполнено с помощью команды «Построение линии тренда» программы Excel. На нижеприведенных рисунках (рис. 2.2 - 2.6 показаны различные регрессионные модели, описывающие связь между двумя заданными последовательностями случайных величин.  Рисунок 2.2 – Экспоненциальная модель  Рисунок 2.3 – Линейная модель 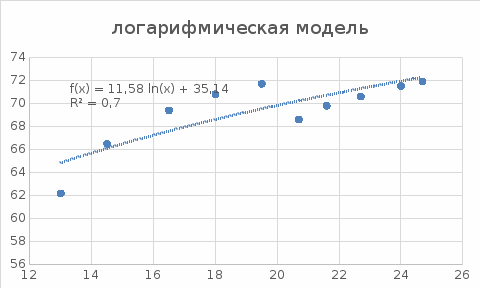 Рисунок 2.4 – Логарифмическая модель  Рисунок 2.5 – Полиномиальная модель  Рисунок 2.6 –Степенная модель В таблице 2.4 показаны сводные данные по всем построенным моделям. Таблица 2.4 - Сводные данные построенных регрессионных моделей
Вывод: проанализировав таблицу видим, что уравнение регрессии лучшим образом аппроксимирует уравнение y = -0,0899x2 + 4,0066x + 26,604, т.к. R² = 0,7985. Заключение: в данной задаче я освоил компетенции выполнения статистического анализа двумерных данных, также выполнил поставленные задачи, а именно: выполнил корреляционный, регрессионный, визуальный анализ двумерной последовательности случайных величин первая – коэффициент пористости, m; вторая - водонасыщенность на фронте, Sф%. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ Реалистичное содержание целевой функции. В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов Xi) Y принята дебит нефтяной скважины, м³/сутки: Реалистичное содержание (сущность) факторов. В качестве факторов функции отклика Xi принимаются: X1 - Забойное давление, МПа; X2 - Диаметр штуцера, мм; Х3 - Температура, °С. Уровни варьирования значений факторов. Минимальные и максимальные значения факторов приняты следующие:
Среднее значение фактора. Среднее значение фактора определяется по формуле: X10 = 3,05; X20 = 12; X30 = 78. Интервалы варьирования фактора. Интервал варьирования определяется по формуле: dx1 = X10 – X1min = 2, 95. dx2 = X20 – X2min = 8. dx3 = X30 – X3min = 43. Корректность определения значений факторов.
Нормированные значения факторов. Нормированные значения определяются формулой:  . .Хн1 = (6 - 3,05) /2,95 = 1; Хн2 = (20 – 12) /8 = 1; Хн3= (121 – 78) /43 = 1. Матрица планирования полного факторного эксперимента. Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен, и равен 1.
Экспериментальные значения целевой функции.
Расчет среднего арифметического результатов каждого опыта.
Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта). Дисперсия среднего арифметического определяется формулой:  где m – количество параллельных опытов в строке матриц.
Оценка однородности построчных дисперсий. Расчетное значение критерия Кохрена. Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:  где smax – наибольшая величина дисперсии; si – дисперсия i-го опыта N – Общее число опытов в матрице. Максимальное значение дисперсии результатов опыта: S2ymax= 0, 11477. Сумма всех построчных дисперсий:  S2 y = 0,00892+0,05823+0,02503+0,11477+0,03487+0,08425+0,09508+0,03147 = 0,45262. S2 y = 0,00892+0,05823+0,02503+0,11477+0,03487+0,08425+0,09508+0,03147 = 0,45262.Расчетное значение критерия Кохрена: Gp= 0, 11477/0, 45262 = 0, 25. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N, где N – число опытов (количество строк в матрице планирования). Табличное значение критерия Кохрена. Уровень значимости. = 0,05. Степень числителя (f1): f1= m –1= 4, где m – количество параллельных опытов в строке матриц Степень свободы знаменателя (f2): f2 = N = 8, где N – общее число опытов в матрице. Табличное значение критерия Кохрена Gт = 0,3910. Вывод: Так как расчетное значение критерия Кохрена меньше табличного (0,3910 <2,01), следовательно, дисперсия экспериментальных значений функции отклика однородны Вид уравнения регрессии, принятого для построения модели функции отклика. Рекомендуется полиномиальная модель функции отклика y = b0 X0 + b1 X1 + b2 X2 + b3 X3 +b12 X1Х2+b13 X1Х3+b23 X2Х3+b123 X1 X2Х3 . Коэффициенты регрессии. Значения коэффициентов регрессии определяются по формулам:  ; ; и так далее для всех коэффициентов. Таблица - Значения коэффициентов регрессии.
Статистическая значимость коэффициентов регрессии. Расчетные значения критерия Стьюдента. Оценка производится по t-критерию Стьюдента. Проверяется отклонение от нуля найденной оценки. Для каждого коэффициента bk вычисляется расчетное значение критерия Стьюдента:  ; ;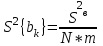 ; ;где bk – коэффициент уравнения регрессии; S{bk} – оценку дисперсию коэффициентов, найденных по экспериментальным данным; 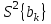 - дисперсия коэффициентов, найденных по экспериментальным данным; - дисперсия коэффициентов, найденных по экспериментальным данным;S2b = 0,00892+0,05823+0,02503+0,11477+0,03487+0,08425+0,09508+0,03147/8 = 0,056578 . S2{bk} = 0,056578/(8*5) = 0,0014. S{bk} = 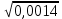 = 0.0374 = 0.0374Расчетные значения критерия Стьюдента
Табличные значения критерия Стьюдента. Уровень статистической значимости. = 0,05 . Степень свободы f = N (m-1) = 8*(5-1) = 32. табличное значение коэффициента равно tт = 2,04 Функция отклика со статистически значимыми коэффициентами. Функция отклика со статистически значимыми коэффициентами имеет вид: y = b0 X0 + b1 X1 + b2 X2 + b3 X3 +b12 X1Х2+b13 X1Х3+b23 X2Х3+b123 X1 X2Х3 Значения функции отклика для каждого опыта по новой функции отклика со статистически значимыми коэффициентами.
Проверка адекватности новой функции отклика со статистически значимыми коэффициентами. Расчетное значение критерия Фишера (F- критерия). Адекватность модели проверяют по критерию Фишера, расчетное значение которого определяется по формуле: Fp= S2ад/S2в ; 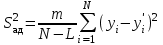 ; ;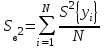 , ,где L – число значимых коэффициентов. m – количество параллельных опытов в строке матриц m/(N-L) = 5/ (8-3) = 1 S2ад = 1*((20,575-20,575)2+ (21,496-24,382)2+ (22.736-26,304)2+ (23.348-22,736)2+ (24.382-25,64)2+ (25.64-21,496)2+ (26.304-23,348)2+ (27.588-27,588)2) = 48,93; S2в = 0,00892+0,05823+0,02503+0,11477+0,03487+0,08425+0,09508+0,03147/8 = 0,056578; Fp = 48,93/0.056578 = 864,77. Уровень значимости = 0.05. Степень свободы адекватности: fад = N – l = 8-1 = 7. Степень свободы воспроизводимости: fв = = N(m - 1) = 8*(5-1) = 32. Табличное значение критерия Фишера. Fт = 3,2. Вывод: Сравнив расчетное значение критерия с табличным делаем вывод об адекватности модели, так как Fp> Fт, то полученная математическая модель с принятым уровнем статистической значимости неадекватна экспериментальным данным. Следовательно, при выбранном уровне статистической значимости полученная в результате эксперимента регрессионная модель вида y = 24,00825+ 0,50975 X1н + 0,98575X2н + 1,97025X3н + (-0,0,3575 X1Х2)+ 0,12575 X1Х3+(-0,01825 X2Х3)+0,04225 X1 X2Х3 неадекватна исследуемому объекту Функция отклика со статистически значимыми коэффициентами и натуральными факторами. Функция отклика со статистически значимыми коэффициентами и натуральными факторами имеет вид: Y = b0 + b1  + b2 + b2 + b12 + b12   = 24,00825+0,50975*((6-3,05)/2,95)+0,98575*((20-12)/8)+(-0,0357*((6-3,05)/2,95)*((20-12)/8)) = 25,46805. Заключение В процессе контрольной работы была построена целевая функция, характеризующая зависимость дебита нефтяной скважины от трёх факторов: забойного давления, диаметра штуцера, температуры. Для её построения были проведены стандартные статистические характеристики. За основу целевой функции была принята полиноминальная регрессионная модель. Мною были освоены компетенции по планированию эксперимента и обработке его результатов. ЛитератураСидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399 с. 2.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479 с. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476 с. Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с. (электронный ресурс). Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976. Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983. Налимов В.В. Теория эксперимента. М.: Наука, 1971. Планирование и организация измерительного эксперимента / Е.Т. Володаpский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
