егэ. Теория игр. Поиск выигрышной стратегии
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Ещё пример задания:P-00(демо-2021).Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней. В начальный момент в первой куче было семь камней, во второй куче – S камней; 1 ≤ S ≤ 69. Задание 19. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна. В задачах такого типа «неудачным» считается такой ход Пети, после которого он проиграет, хотя мог бы выиграть, ИЛИ... он проиграет быстрее (за меньшее число ходов) чем мог бы, если бы старался затянуть игру. Задание 20. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: − Петя не может выиграть за один ход; − Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания. Задание 21 Найдите минимальное значение S, при котором одновременно выполняются два условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Решение (программа, А. Кабанов) Напишем функцию, которая определяет существование выигрышной стратегии не более чем за moveWin ходов обоих игроков. Функция имеет четыре параметра: количество камней в первой куче a, количество камней во второй куче b, число совершённых ходов prevMoves и наибольшее возможное количество ходов moveWin. def f( a, b, prevMoves, moveWin ): if a + b >= 77: return prevMoves % 2 == moveWin % 2 # 1 if prevMoves == moveWin: return 0 # 2 h = [ f(a+1, b, prevMoves+1, moveWin), # 3 f(a, b+1, prevMoves+1, moveWin), f(a*2, b, prevMoves+1, moveWin), f(a, b*2, prevMoves+1, moveWin)] return any(h) if (prevMoves+1) % 2 == moveWin % 2 \ # 4 else all(h) Если moveWin нечётное, то проверяется возможность победы первого игрока, для чётных победа второго игрока. (метка #4). При анализе следующих ходов мы исходим из принципа, что если их чётность совпадает с moveWin, то достаточно победы в одном из них. В противном случае победа должна быть во всех случаях (метка #4). Для удобства можно составить список из значений функций для следующих ходов. Для проверки условий можно использовать any и all (метка #4). Для выполнения 19 задания создадим функцию f1 аналогичную f, кроме замены последней строки на return any(h) для поиска победы хотя бы при одном из ходов противника и найдём минимальное значение с выигрышной стратегией за 2 хода. print('19)', min(s for s in range(1,70) if f1(7,s,0,2)) ) Для нахождения ответа на 20 задание найдём значения S, для которых не существует выигрышной стратегии за 1 ход, но существует за 3 хода. print('20)', *[s for s in range(1,70) if not f(7,s,0,1) and f(7,s,0,3)]) Для нахождения ответа на 21 задание найдём значение S, для которого не существует выигрышной стратегии за 2 хода, но существует за 4 хода. print('21)', min(s for s in range(1,70) if not f(7,s,0,2) and f(7,s,0,4))) Ответ: 19) 18 20) 31 34 21) 30 Решение Задания 19. возможно, что есть несколько значений S, которые удовлетворяют условию; нас интересует минимальное из них; при минимальном подходящем значении S общее количество камней в двух кучах увеличивается максимально быстро до значения 77 или большего; поскольку удвоение увеличивает количества камней в куче быстрее, чем добавление одного камня, можно сделать вывод, что для минимального подходящего значения S игроки своими ходами дважды удвоили бОльшую из двух куч; предположим, что бОльшая куча имеет 7 камней, и S = 7; тогда наибольшее число камней, которое можно получить после одного хода каждого игрока – 7 + 7*2*2 = 35; так как 35 < 77, игра не окончена и этот вариант не подходит; делаем вывод, что S > 7 таким образом, дважды была удвоена вторая куча; условие окончания игры 7 + S*2*2 77, откуда получаем S 17,5; это значит, что Smin = 18 Ответ: 18. Решение Задания 20. Петя своим ходом должен перевести игру в такую позицию, что Ваня не может выиграть своим первым ходом, но добавление одного камня в любую кучу позволяет выиграть Пете вторым ходом рассмотрим такие (проигрышные) позиции; при удвоении второй (бОльшей) кучи в сумме должно получаться 76 камней (недостаточно для выигрыша): (8, 34) (10, 33) (12, 32) (14,31) (16,30) … теперь подумаем, какие из них можно получить из начальной позиции (7, S) за один ход; видно, что количество камней в первой куче изменяется, то есть Петя на первом ходу работает с первой кучей; он может получить там 7 + 1 = 8 камней (и у нас есть критическая позиция (8,34)!) или 7*2=14 камней (для этого случая тоже есть критическая позиция (14,31)) поэтому условию задания удовлетворяют значения S = 31 и 34, их нужно записать в порядке возрастания Ответ: 31 34. Решение Задания 21 (благодарю за обсуждение Д. Муфаззалова и В. Бабия). определим свойства позиции, которую мы ищем: это проигрышная позиция, то есть всех возможные ходы из нее ведут в выигрышные позиции; из этой позиции есть ход в выигрышную позицию, из которой Ваня не может выиграть за один ход, но может гарантированно выиграть за два; это значит, что есть ход в позицию, определённую в решении задачи 20 или равноценную ей! для полного решения задачи построим таблицу выигрышных и проигрышных позиций; выигрышные позиции будем обозначать положительными числами, например, 2 – выигрыш в два хода; проигрышные позиции обозначаем отрицательными числами, например, «–2» – проигрыш в два хода (это значит, что при самой лучшей игре первого игрока второй выиграет по крайней мере своим вторым ходом) таблица будет прямоугольная, на вертикальной оси откладываем количество камней в первой куче, на горизонтальной – количество камней во второй куче:
пока в таблице расставлены единицы в позициях, которые ведут к выигрышу Пети на первом ходу и «–1» в позициях, которые ведут к выигрышу Вани на своем первом ходу (после любого первого хода Пети) отметим числом 2 ячейки, откуда есть ходу в серые клетки с ходом «–1»:
в верхней строке таблицы выделены жёлтым позиции (7, 31) и (7, 34), найденные при решении предыдущего задания докажем, что в верхней строке больше нет позиций с кодом 2; по определению из позиции с кодом 2 есть ход в позицию с кодом «–1»; во всех позициях с кодом «–1», не попавших в рассмотренную часть таблицы, в первой куче больше 14 камней, то есть, стартовав с первой кучей из 7 камней мы не можем получить такие позиции за один ход нам нужно найти в верхней строке позиции, из которых все ходы ведут в выигрышные позиции с кодами 1 (выигрыш за 1 ход) или 2 (выигрыш за 2 хода) сразу видны две таких позиции (выделены на следующем рисунке зелёным цветом): (7, 30) – возможные ходы в (7, 31), (8, 30) и (14, 30) с кодом 2 и (7, 60) с кодом 1 (7, 33) – возможные ходы в позиции (7, 34) и (8, 33) с кодом 2, а также (14, 33) и (7, 66) с кодом 1:
вроде бы все хорошо, и можно выбрать минимальное из двух найденных значений S (30), но кроме этих ячеек есть ещё кандидат на решение – S = 17, потому что ходом из позиции (7, 17) можно получить позицию (7, 34) с кодом 2 однако на самом деле позиция (7, 17) нам не подходит, докажем это, рассмотрев все возможных ходы Пети: (8, 17) (14, 17) (7, 18) (7, 34) здесь жёлтым фоном выделены ходы с кодом 2 – выигрышные позиции за 2 хода (из позиции (8, 17) есть ход в (8, 34) с кодом «–1») рассмотрим ход (14, 17); возможные ходы из него (15, 17) (28, 17) (14, 18) (14, 34) среди них нет ни одного хода в позицию с кодом «–1», то есть, ход Пети (14, 17) не даст Ване выиграть за 2 хода; поэтому эта позиция не подходит Ответ: 30. Решение с помощью программы (рекурсия) напишем программу на языке Python, которая для всех значений S выдаёт код позиции (про коды позиций см. выше) сначала поясним идею; пусть нужно определить код позиции (x, y); для этого мы должны предварительно определить коды позиций, куда можно попасть одним ходом из (x, y): (x+1, y) (2x, y) (x, y+1) (x, 2y) поскольку нужно выполнить ту же самую операцию, это будет рекурсивная функция итак, пусть мы нашли коды четырёх возможных следующих позиций; рассмотрим несколько примеров: пусть эти коды [1, 2, 2, 3], то есть все возможные ходы ведут в выигрышные позиции, Петя проигрывает; он заинтересован в том, чтобы проиграть за максимальное число ходов (всячески оттягивая поражение), поэтому из этих кодов нужно выбрать максимальный и записать его со знаком минус, получаем код «–3», то есть Петя проиграет за 3 хода (на 3-м ходу Ваня выиграет) пусть эти коды [1, –2, 2, –3], то есть найдены два хода в проигрышные позиции (с кодами «–2» и «–3»), и Петя может выиграть; он заинтересован в том, чтобы выиграть за наименьшее число ходов, поэтому нужно выбрать максимальное из полученных отрицательных чисел («–2»), убрать знак минус и добавить единицу (Петя добавляет новый ход); поэтому для данного случая код клетки будет равен 3 рекурсия должна заканчиваться, когда сумма x+yстала больше или равна 77; определим это значение как константу TARGET («цель»); TARGET = 77 такую позицию (когда игра завершена) будем обозначать кодом 0 и считать её проигрышной, как и позиции с отрицательным кодом запишем первую версию функции gameResult, которая принимает два параметра - количество камней в первой и второй кучах: def gameResult( x, y ): if x + y >= TARGET: return 0 # рекурсивно определяем коды всех возможных ходов nextCodes = [ gameResult(x+1, y), gameResult(x*2, y), gameResult(x, y+1), gameResult(x, y*2) ] if в nextCodes есть отрицательные или 0: res = -max(отрицательные или 0) + 1 else: res = -max(nextCodes) return res строки, выделенные красным цветом – это псевдокод, который нужно заменить на операторы Python; выделим из массива nextCodes все отрицательные числа и нули (соответствующие проигрышным позициям): negative = [c for c in nextCodes if c <= 0] тогда условный оператор if в nextCodes есть отрицательные или 0: может быть записан как if negative: res = -max(negative) + 1 else: res = -max(nextCodes) получается такая функция: def gameResult( x, y ): if x + y >= TARGET: return 0 # рекурсивно определяем коды всех возможных ходов nextCodes = [ gameResult(x+1, y), gameResult(x*2, y), gameResult(x, y+1), gameResult(x, y*2) ] negative = [c for c in nextCodes if c <= 0] if negative: res = -max(negative) + 1 else: res = -max(nextCodes) return res попробуем посчитать коды для всех возможных значений S от 69 = 77-7-1 до 1: X = 7 for S in range(TARGET-X-1,0,-1): r = gameResult( X, S ) print( "{:d} {:d}".format(S, r) ) к сожалению, обнаруживаем, что программа работает очень медленно… Дело в том, что программа много раз вычисляет значение кода для одних и тех позиций. Чтобы этого избежать, будем запоминать их в словаре results: results = {} # (1) def gameResult( x, y ): if (x,y) in results: return results[(x,y)] # (2) if x + y >= TARGET: return 0 nextCodes = [ gameResult( x+1, y ), gameResult( x*2, y ), gameResult( x, y+1 ), gameResult( x, y*2 ) ] negative = [c for c in nextCodes if c <= 0] if negative: res = -max(negative) + 1 else: res = -max(nextCodes) results[(x,y)] = res # (3) return res добавленные строчки выделены голубым фоном; в строке (1) создаётся пустой словарь (глобальная переменная), ключом в этом словаре будет кортеж, описывающий позицию (x, y); в строке (2) мы проверяем, нет ли в словаре кода для запрошенной позиции; если есть, то сразу возвращаем этот код в строке (3) добавляем в словарь новый код запрошенной позиции теперь программа отрабатывает очень быстро, и мы видим, что позиция (7, 17), которую мы хотели проверить, на самом деле выигрышная (её код 11); это значит, что ответ на вопрос задачи 21 – это 30. Ответ: 30. Решение с помощью программы (рекурсия, 2-й вариант) введём константы: количество камней в первой куче, цель игры, N1, TARGET = 7, 77 количество камней, которые можно добавить, и коэффициент, на который можно умножить количество камней в любой куче: KADD, KMUL = 1, 2 определим вспомогательную функцию gameOver, которая возвращает истинное логическое значение (True), если игра окончена: def gameOver( n1, n2 ): return n1+n2 >= TARGET определим функцию win(n1,n2,byMove), которая возвращает истинное логическое значение (True), если в позиции (n1,n2) можно гарантированно выиграть не более чем за byMove ходов: def win( n1, n2, byMove ): if gameOver(n1, n2): return False return lose( n1+KADD, n2, byMove-1 ) or \ lose( n1*KMUL, n2, byMove-1 ) or \ lose( n1, n2+KADD, byMove-1 ) or \ lose( n1, n2*KMUL, byMove-1 ) В первой строке проверяется условие окончания игры: если игра окончена, то тот, чья очередь ходить в этой позиции, проиграл: if gameOver(n1, n2): return False Игрок выигрывает в некоторой позиции не более чем за byMove ходов, если все его возможные ходы ведут в проигрышные (для соперника) позиции, причем при любом ходе соперник проигрывает не более чем за byMove-1 ходов: return lose( n1+KADD, n2, byMove-1 ) or \ lose( n1*KMUL, n2, byMove-1 ) or \ lose( n1, n2+KADD, byMove-1 ) or \ lose( n1, n2*KMUL, byMove-1 ) Здесь вызывается функция lose(n1,n2,byMove), которую мы напишем далее. Она возвращает истинное логическое значение (True), если в позиции (n1,n2) игрок гарантированно проиграет не более чем за byMove ходов. Обратите внимание на логическую операцию or: для выигрыша достаточно, чтобы хотя бы один ход создавал проигрышную позицию для соперника. функция lose выглядит так: def lose( n1, n2, byMove ): if gameOver(n1, n2): return True if byMove == 0: return gameOver(n1, n2) return win( n1+KADD, n2, byMove ) and \ win( n1*KMUL, n2, byMove ) and \ win( n1, n2+KADD, byMove ) and \ win( n1, n2*KMUL, byMove ) Сначала проверяется, не закончилась ли уже игра. Если это случилось, возвращается значение True: тот, кто получил такую позицию, проиграл. Если уже не осталось ходов (byMove==0), результат работы функции равен False: игра окончена, а ходов уже нет. В общем случае проверяем возможные ходы: если все они приводят к выигрышу соперника не более чем за byMove ходов, то позиция проигрышная, причем проигрыш наступит не позже, чем хода с номером byMove (дольше сопротивляться не получится). Обратите внимание на логическую операцию and: для проигрыша необходимо, чтобы все ходы вели в выигрышную позицию для соперника. ответ на вопрос задания 19 строится так же, как было показано выше; для округления вверх используется функция ceil из модуля math: from math import ceil ans1 = min( ceil((TARGET-N1)/KMUL/KMUL), ceil(TARGET-N1*KMUL*KMUL) ) значения s, при которых выполняются условия заданий 20 и 21, находятся в цикле: for s in range(18,TARGET-N1+1): if win(N1, s, 2) and not win(N1, s, 1): ans2.append(s) if lose(N1, s, 2) and not lose(N1, s, 1): ans3.append(s) Массив ans2 содержит все значения s, при которых есть стратегия выигрыша в 2 хода, но нет стратегии гарантированного выигрыша за 1 ход; массив ans3 содержит все значения s, при которых тот, кто начинает игру, проигрывает за 2 хода, но не всегда проиграет за 1 ход. полная программа на Python: N1, TARGET = 7, 77 KADD, KMUL = 1, 2 def gameOver( n1, n2 ): return n1+n2 >= TARGET def win( n1, n2, byMove ): if gameOver(n1, n2): return False return lose( n1+KADD, n2, byMove-1 ) or \ lose( n1*KMUL, n2, byMove-1 ) or \ lose( n1, n2+KADD, byMove-1 ) or \ lose( n1, n2*KMUL, byMove-1 ) def lose( n1, n2, byMove ): if gameOver(n1, n2): return True if byMove == 0: return False return win( n1+KADD, n2, byMove ) and \ win( n1*KMUL, n2, byMove ) and \ win( n1, n2+KADD, byMove ) and \ win( n1, n2*KMUL, byMove ) from math import ceil ans1 = min( ceil((TARGET-N1)/KMUL/KMUL), ceil(TARGET-N1*KMUL*KMUL) ) ans2, ans3 = [], [] for s in range(18,TARGET-N1+1): if win(N1, s, 2) and not win(N1, s, 1): ans2.append(s) if lose(N1, s, 2) and not lose(N1, s, 1): ans3.append(s) print("--- Ответы ---") print("19. ", ans1) print("20. ", sorted(ans2)) print("21. ", ans3) Решение на языке PascalABC.NET: в целом решение повторяет приведённое выше решение на Python для хранения уже полученных результатов используется словарь memory, в котором каждой паре чисел, задающих количество камней в двух кучах (тип tuple) сопоставляется целое число – оценка позиции: type tuple = (integer, integer); const TARGET = 77; var memory: Dictionary function gameResult( x, y: integer ): integer; begin if (x, y) in memory then begin result := memory[(x,y)]; exit; end; if x+y >= TARGET then begin result := 0; exit; end; var next := | gameResult(x+1,y), gameResult(x,y+1), gameResult(2*x,y), gameResult(x,2*y)|; var negative := next.Where(x->x<=0).ToArray; if negative.Length > 0 then result := - negative.Max + 1 else result := - next.Max; memory[(x,y)] := result; end; begin var X:= 7; memory := new Dictionary for var s:=TARGET-X-1 downto 1 do Println( s, gameResult(x,s) ); end. Решение с помощью программы (динамическое программирование, А. Сидоров) вместо рекурсии можно применить динамическое программирование, где вместо словаря results используется двухмерный массив: TARGET = 77 results = [[0]*2*TARGET for i in range(2*TARGET)] for x in range(TARGET-1,0,-1): for y in range(TARGET-x-1,0,-1): nextCodes = [ results[x+1][y], results[2*x][y], results[x][y+1], results[x][2*y]] negative = [с for с in nextCodes if с <= 0] if negative: results[x][y] = -max(negative) + 1 else: results[x][y] = -max(nextCodes) N1 = 7 for S in range(TARGET-N1-1,0,-1): print( "{:d} {:d}".format(S, results[N1][S]) ) Эта программа для каждого значения S выводит оценку позиции. Положительные значения K означают выигрыш: Петя выиграет за K ходов. Отрицательные значение (-K): Ваня гарантированно выиграет не позднее, чем своим K-м ходом. Ответ: 30. Решение с помощью электронных таблиц (А. Кабанов) Для начала отметим комбинации камней, из которых игрок побеждает своим первым ходом. Составим таблицу, в которой по вертикали отметим камни в первой куче камней (начиная с 7), а по горизонтали – во второй куче камней (начиная с 1).  Для каждой пары рассчитаем максимальное число камней, которое может получить игрок за один ход. Для этого необходимо большую из куч умножить на два. В ячейке B2 запишем формулу =МАКС(2*$A2+B$1;$A2+2*B$1) и заполним ей всю нашу таблицу. Далее с помощью условного форматирования пометим ячейки, в которых сумма не менее 77 (условие выигрыша). 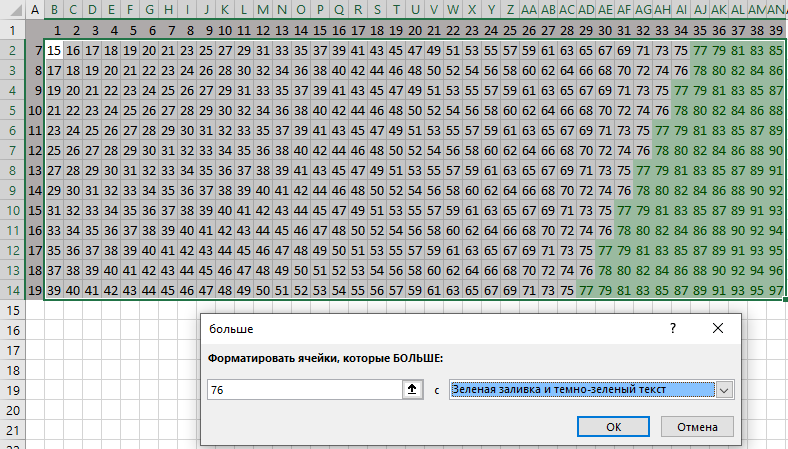 Решение 19 задания: Для решения 19 задания рассмотрим две ситуации: а) Петя умножает вторую кучу на 2, а Ваня выигрывает первым ходом. Ход Пети имеет вид (7;S) →(7;2S). Ваня будет выигрывать первым ходом, если 2S ≥35 (см. таблицу) или S≥18. б) Петя умножает первую кучу на 2, а Ваня выигрывает первым ходом. Ход Пети имеет вид (7;S) →(14;S). Ваня будет выигрывать первым ходом, если S ≥32 (см. таблицу). Нетрудно видеть, что минимальное подходящее значение S равно 18. Ответ: 18. Решение 20 задания: Для начала найдём проигрышные значения (при любой игре побеждает следующий игрок). Рассмотрим комбинации (K; S) из которых каждый ход вида (K; S+1) (K+1; S) (2K; S) (K; 2S) попадает в выигрышные позиции. 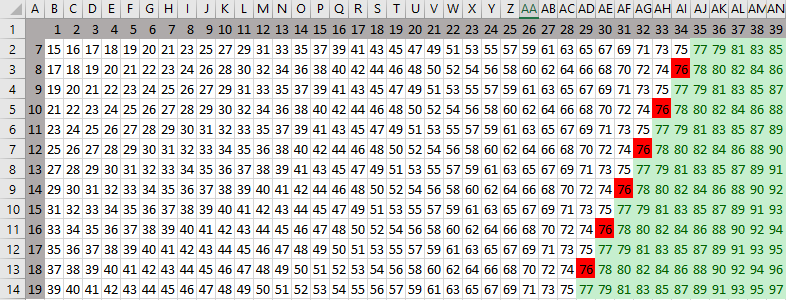 Петя будет гарантированно побеждать своим вторым ходом, если его первый ход попадает в отмеченные проигрышные значения. Рассмотрим ситуации, когда победный ход Пети (K+1;S) или (K;S+1). Отметим в таблице ячейки, из которых возможны такие ходы. 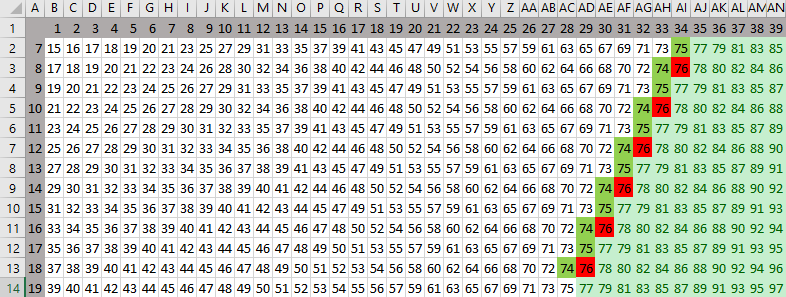 Рассмотрим ситуации, когда победный ход Пети (2K; S) или (K;2S). Выпишем все проигрышные позиции: (8;34) (10;33) (12;32) (14;31) (16;30) (18;29) … Для каждой из них выпишем, позиции с вдвое меньшим числом камней в одной из куч (если такая позиция возможна): (8;34) – (8;17) (12;32) – (12;16) (14;31) – (7;31) (16;30) – (8;30) (16;15) (18;29) – (9;29) Также отметим их на таблице (остальные по необходимости добавляются по аналогии) 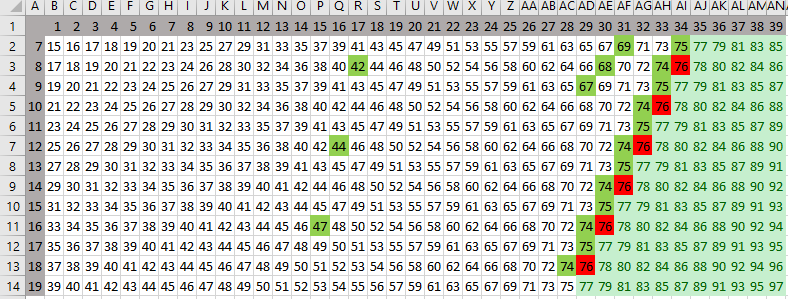 Интерес представляют значения, где первая куча равна 7, поэтому: Ответ: 31 34. Решение 21 задания: Рассмотрим комбинации вида (7;S), ходы (K+1;S) и (K;S+1) из которых попадает в выигрышные позиции. По таблице видно, что это (7;33) и (7;30). Проверим их: – Из (7;33) Петя может сходить в (7;34) (8;33) – победа Вани 2 ходом и (7;66) (14;33) – победа Вани 1 ходом. – Из (7;30) Петя может сходить в (7;31) (8;30) (14;30) – победа Вани 2 ходом и (7;62)– победа Вани 1 ходом. Оба значения подходят и наименьшее из этих значений 30. Ответ: 30. Решение с помощью программы: имитация решения в электронных таблицах (Д. Муфаззалов) Если трудно разобраться в рекурсивном алгоритме или динамическом программировании, можно написать более простую программу, имитирующую решение в электронных таблицах. Вместо таблицы будем использовать двумерный массив: n = 69 target = 77 a = [["--"] * target * 2 for i in range(target * 2)] Найдем игровые ситуации, из которых можно выиграть за 1 ход: for i in range(1,target): for j in range(1,target): if (i + j + 1 >= target or i * 2 + j >= target or i + 2 * j >= target) and i + j < target: a[i][j] = "V1" Введем функцию, возвращающую множество игровых ситуаций, которые можно получить из текущей игровой ситуации: def f(i,j): return set([a[i][j+1], a[i+1][j], a[i*2][j], a[i][j*2]]) Найдем игровые ситуации, из которых игрок проигрывает за один ход: for i in range(1,target): for j in range(1,target): if a[i][j] == "--" and f(i,j)=={'V1'}: a[i][j] = "P1" Найдем игровые ситуации, из которых игрок выигрывает за 2 хода: for i in range(1,target): for j in range(1,target): if a[i][j] == "--" and ("P1" in f(i,j)): a[i][j] = "V2" Найдем игровые ситуации, из которых игрок проигрывает за один или два хода: for i in range(1,target): for j in range(1,target): if a[i][j] == "--" and (f(i,j) == {'V1', 'V2'}): a[i][j] = "P2" Выведем результаты расчетов: for i in range(n+1): print( "%3d" % i, end='' ) print() for i in range(1,n): print( "%3d" % (i ), end='') for j in range(1,n): print( "%3s" % a[i][j], end='') print() 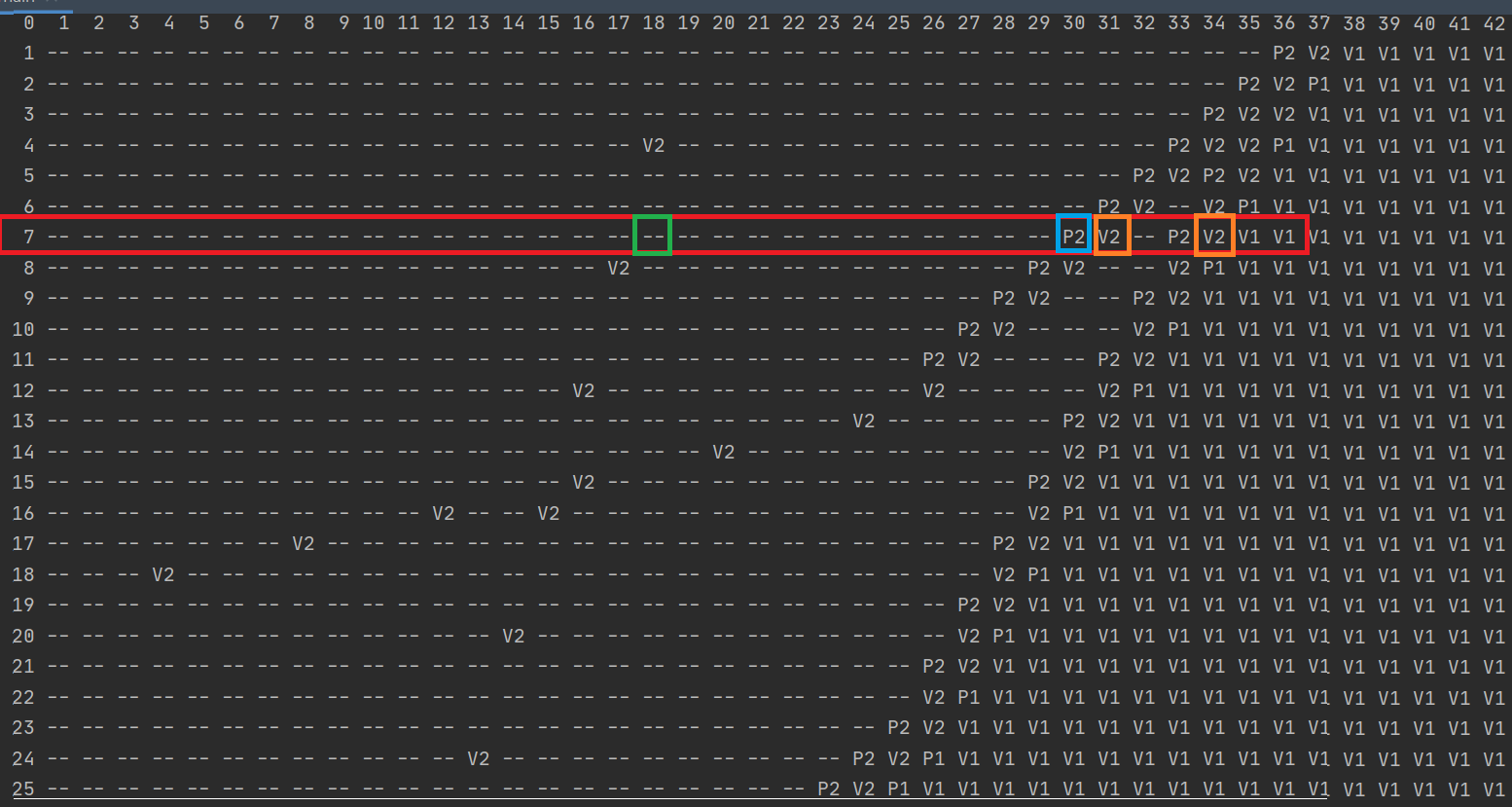 Ответы к заданиям можно получить рассуждениями, приведенными выше. Полная программа: n = 69 tar = 77 a = [["--"] * tar * 2 for i in range(tar * 2)] def f(i,j): return set([a[i][j+1], a[i+1][j], a[i*2][j], a[i][j*2]]) for i in range(1,tar): for j in range(1,tar): if (i + j + 1 >= tar or i * 2 + j >= tar or i + 2 * j >= tar) and i + j < tar: a[i][j] = "V1" for i in range(1,tar): for j in range(1,tar): if a[i][j] == "--" and f(i,j)=={'V1'}: a[i][j] = "P1" for i in range(1,tar): for j in range(1,tar): if a[i][j] == "--" and ("P1" in f(i,j)): a[i][j] = "V2" for i in range(1,tar): for j in range(1,tar): if a[i][j] == "--" and (f(i,j) == {'V1', 'V2'}): a[i][j] = "P2" for i in range(n+1): print( "%3d" % i, end='' ) print() for i in range(1,n): print( "%3d" % (i ), end='' ) for j in range(1,n): print( "%3s" % a[i][j], end='' ) print() |
