Финальный отчёт по ЛР по М ХТП. Ты по
 Скачать 3.92 Mb.
|
|
Расчетные исследования компьютерной модели. Анализ параметрической чувствительности статической модели к изменению давления. %Агумент arg=[1000000 2000000 4000000 6000000 8000000 10000000]; %Функция funk=[8.5829 8.9002 9.169 9.2338 9.4435 9.5331]; %количество точек(рекомендуется 10) n=6; for i=1:n x(i)=arg(i); y(i)=funk(i); end plot(x,y) title('H1=f(p1)') xlabel('p;MPa');ylabel('H;m.'); 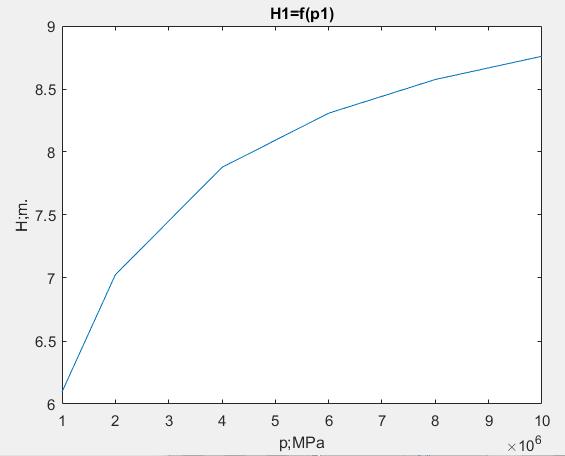 .Анализ параметрической чувствительности статической модели к изменению выходного давления Р5. 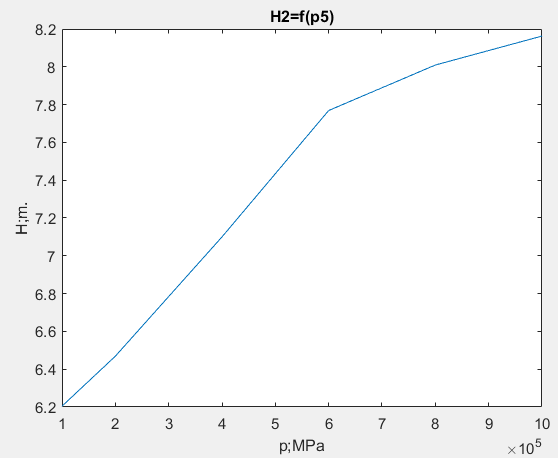 Bывод: Исследована гидравлическая система в статическом режиме. Составлена модель гидравлической системы - условный образ объекта исследования конструированная исследователем так, чтобы отобразить характеристики существенные для исследования. Наилучший порядок решения смогли предположить при помощи информационной матрицы. Также с помощью программы MATLAB установили зависимость между высотами жидкостей в сосудах и давлениями в системе. Была построена математическая модель процесса — это реализованный на ПК алгоритм решения системы уравнений мат. описания. 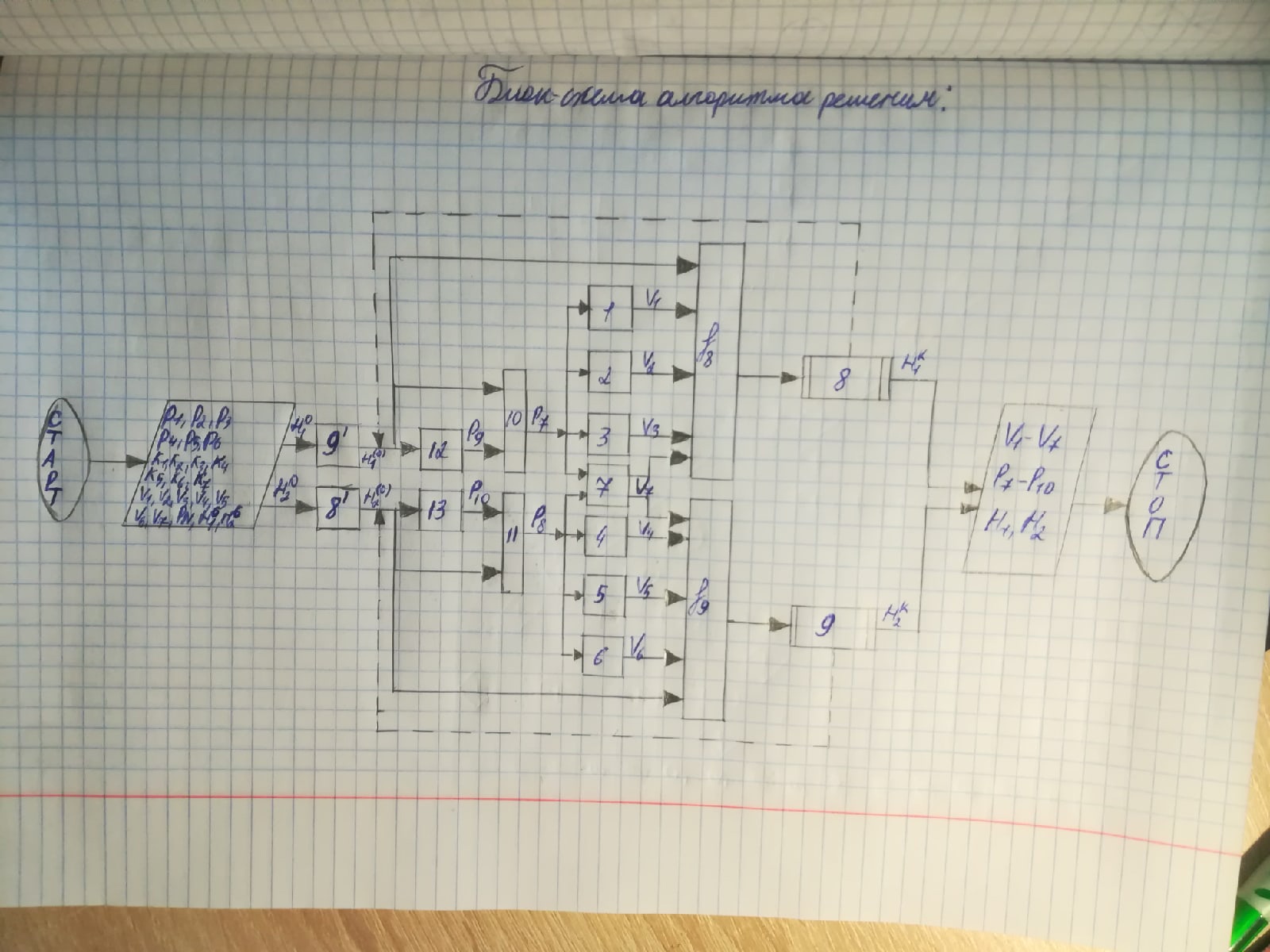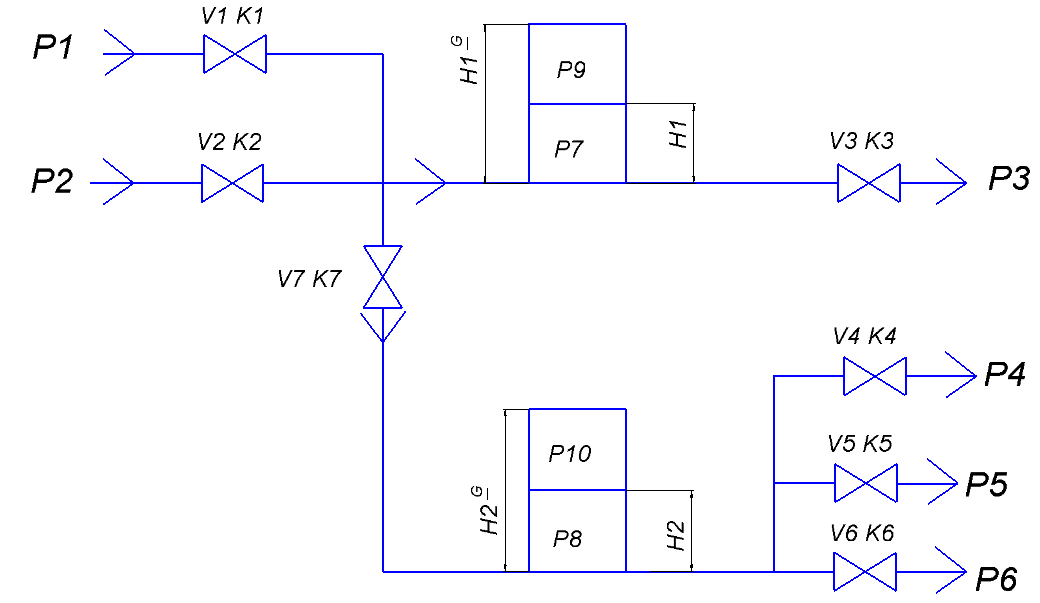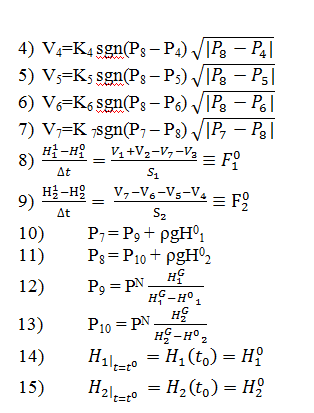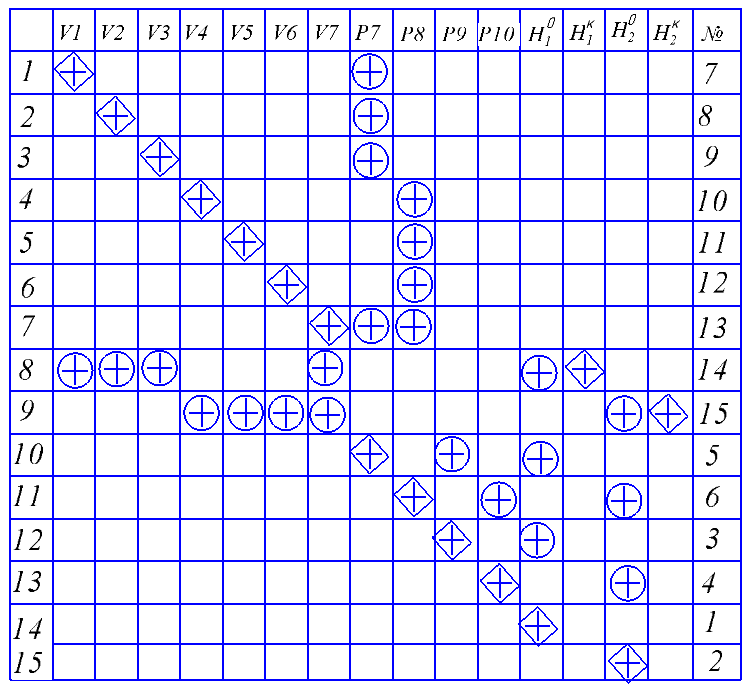Лабораторная работа №2 Компьютерное моделирование простой гидравлической системы в динамическом режиме Вариант № 14      1.Схема гидравлической установки:  Информационная матрицаБлок-схема алгоритма решения 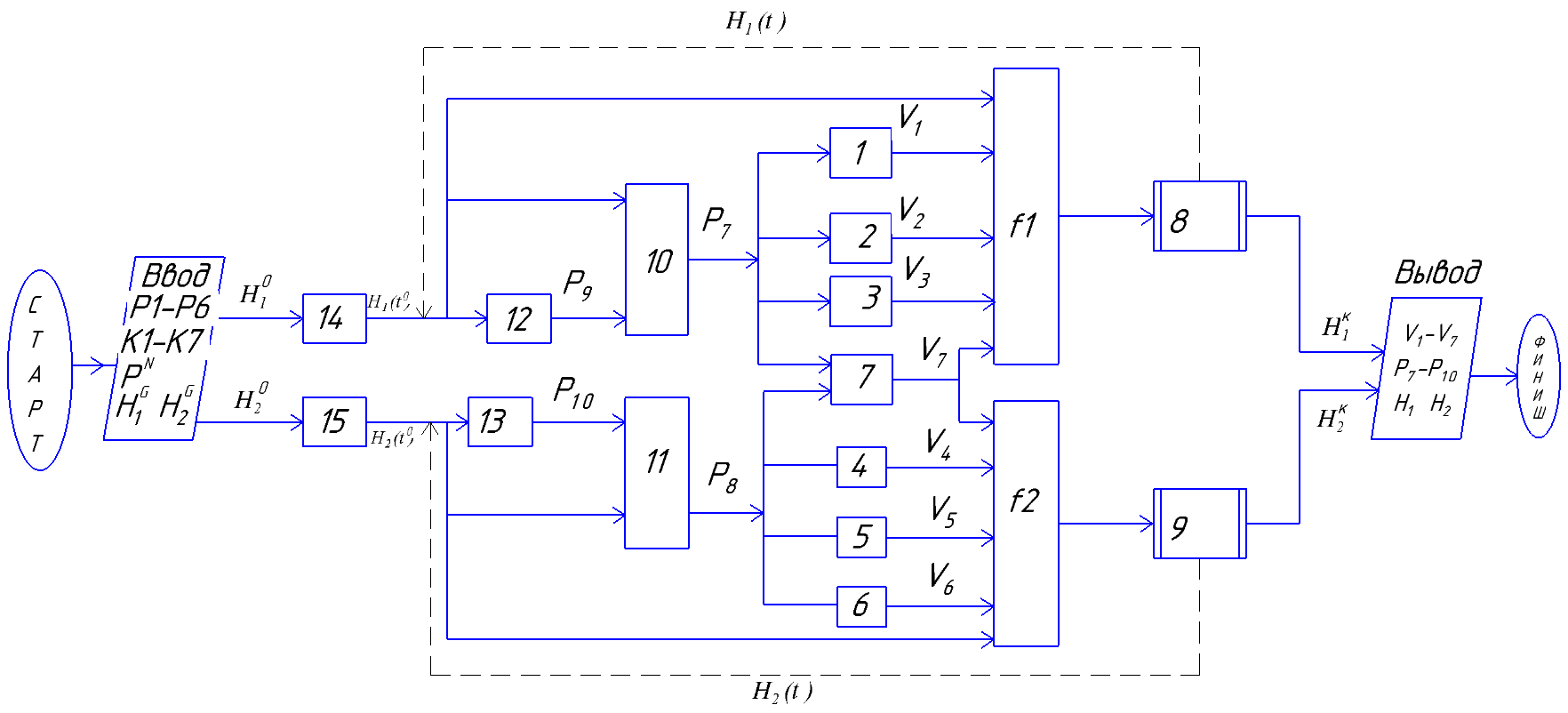 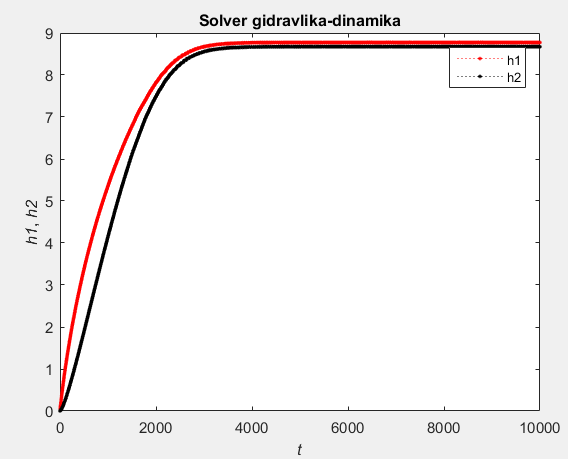 Нормальный режимФункция: function F=fpr(t,h) global ro pn p ak vm hg g v s p(9) = pn * hg(1) / (hg(1) - h(1)); p(10) = pn * hg(2) / (hg(2) - h(2)); p(7) = p(9) + ro * g * h(1); p(8) = p(10)+ ro * g * h(2); v(1) = ak(1) * sign(p(1) - p(7)) * sqrt(abs(p(1) - p(7))); v(3) = ak(3) * sign(p(3) - p(8)) * sqrt(abs(p(3) - p(8))); v(5) = ak(5) * sign(p(8) - p(5)) * sqrt(abs(p(8) - p(5))); v(2) = ak(2) * sign(p(2) - p(7)) * sqrt(abs(p(2) - p(7))); v(4) = ak(4) * sign(p(7) - p(4)) * sqrt(abs(p(7) - p(4))); v(6) = ak(6) * sign(p(8) - p(6)) * sqrt(abs(p(8) - p(6))); v(7) = ak(7) * sign(p(7) - p(8)) * sqrt(abs(p(7) - p(8))); F=[(v(1)+v(2)-v(4)-v(7))/s(1); (v(7)+v(3)-v(6)-v(5))/s(2)]; vm= ro*v end Программа: clc % Динамика global ro pn p ak hg g s np=10; nk=7; nv=13; s=[1,1]; g=9.815; disp ('Высота емкостей'); hg=[10,10]; disp ('плотность (кг/м3)'); ro=1000; disp ('Начальное давление (Па)'); pn=100000; disp ('Площадь внутреннего проходного сечения трубопровода (м^2)'); S=0.01; disp ('Давление (1-4 5-8)'); p=[10000000, 1000000, 1000000, 100000, 100000, 100000, 0, 0, 0, 0]; disp ('Коэф. пропускной способности (1-5)'); k=[0.01, 0.01, 0.01, 0.01, 0.01, 0.03, 0.08]; %время начала исследования процесса t0=0; %время окончания исследования процесса tk=10000; %шаг интегрирования dt=1; t=[t0:dt:tk]; %начальные условия по высотам H10=0;H20=0; Y0=[H10;H20]; for i=1:length(k) ak(i)=k(i)*S/sqrt(ro); end [T,Y]=ode45(@fpr,t,Y0); plot(T,Y(:,1),'r.:') hold on plot(T,Y(:,2),'k.:') title('Solver gidravlika-dinamika') xlabel('\itt') ylabel('{\ith1}, {\ith2}') legend('h1','h2',4) hold off disp('Завершение моделирования') Режим аварийного сброса 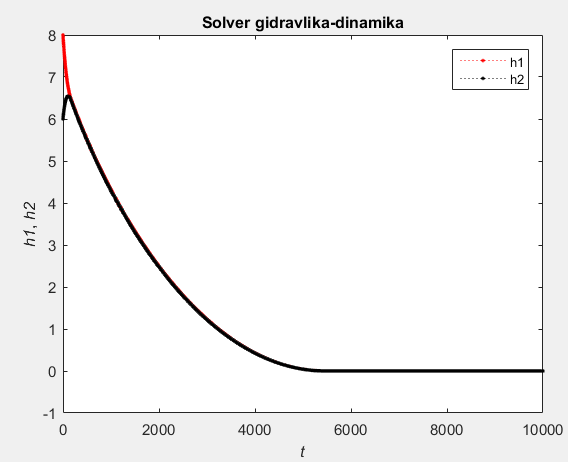 Режим «Аварийного сброса». disp ('Давление (1-4 5-8)'); p=[10000000, 1000000, 1000000, 100000, 100000, 100000, 0, 0, 0, 0]; disp ('Коэф. пропускной способности (1-5)'); k=[0, 0, 0, 0.02, 0.01, 0.01, 0]; %время начала исследования процесса t0=0; %время окончания исследования процесса tk=6000; %шаг интегрирования dt=1; t=[t0:dt:tk]; %начальные условия по высотам H10=9;H20=7; Вывод: Была исследована гидравлическая система в динамическом режиме. Составили модель гидравлической системы - условный образ объекта исследования конструированная исследователем так, чтобы отобразить характеристики существенные для исследования. Наилучший порядок решения смогли предположить при помощи информационной матрицы. Были рассмотрены нормальный режим и режим «Аварийного сброса». Построена математическая модель процесса -реализованный на ПК алгоритм решения системы уравнений мат. описания. Лабораторная работа №3 Краткий отчет по теме «Обработка данных пассивного эксперимента» Вариант № 28
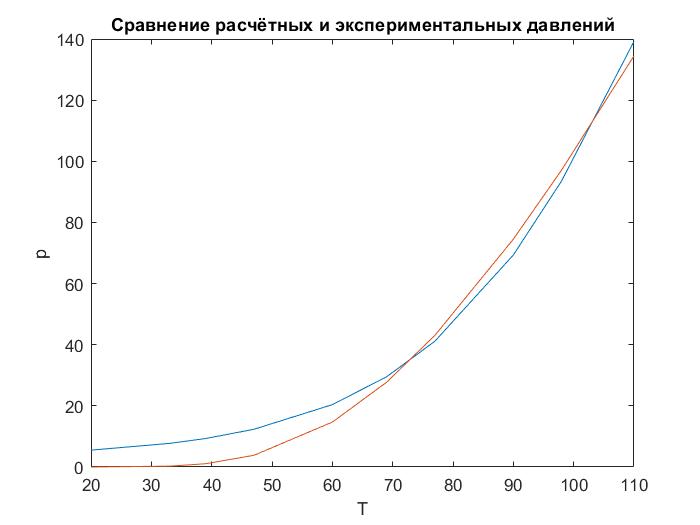 График №1 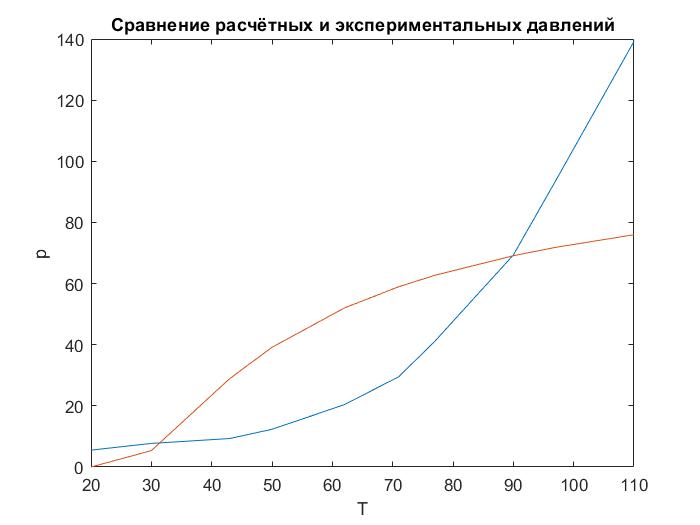 График №2 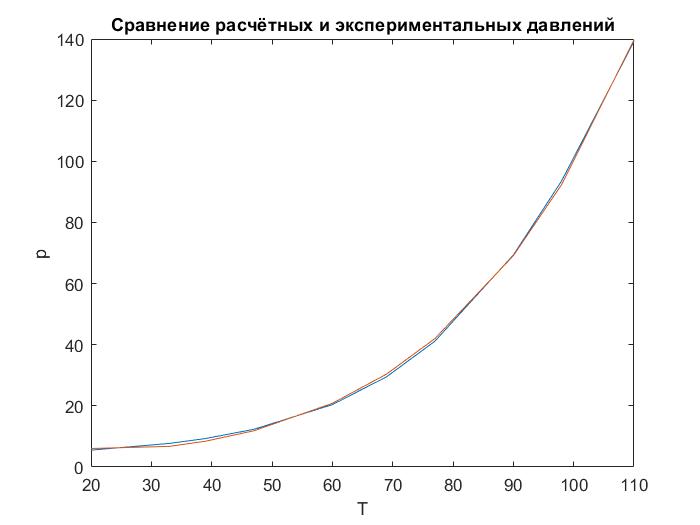 График №3 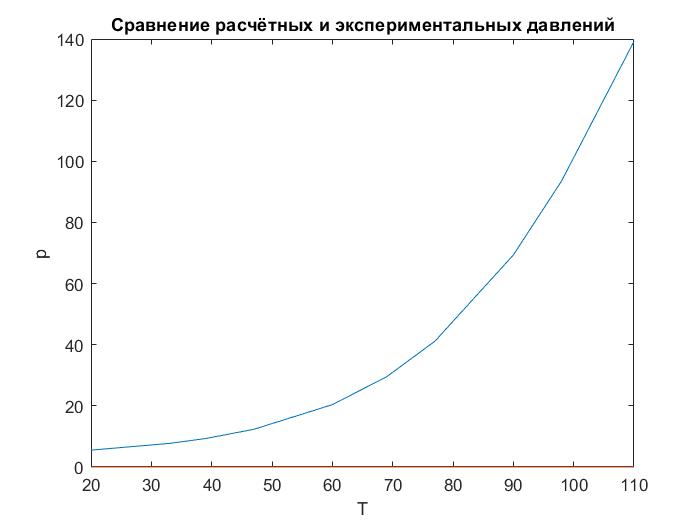 График №4 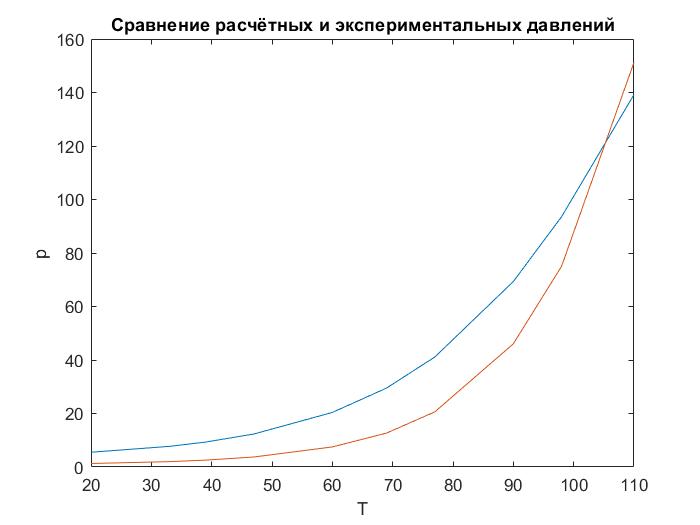 График №5 Вывод: по экспериментальным данным и предложенным моделям уравнений регрессии в данной работе определили коэффициенты этих уравнений. Наиболее адекватной моделью является № 3 т.к. у него наименьшая дисперсия из представленных моделей -S=5.70146, построили сравнительный график экспериментальных данных и расчетных данных по всем пяти уравнениям. 0 |