Учебнометодическое пособие по проведению практических занятий по дисциплине Инженерная геодезия

• Название: Учебнометодическое пособие по проведению практических занятий по дисциплине Инженерная геодезия
• Дата: 26.11.2022
• Размер: 1.24 Mb.
• Имя файла: Fatykhova.docx
• Тип: Учебно-методическое пособие; #813687
• страница: 11 из 21

Обработка результатов теодолитной съемки

Последовательность обработки данных измерений следующая

1. 
   Вычисляется сумма измеренных углов по всему ходу
   

Σβ_изм.= β₁ + β₂ + β₃, где β₁,β₂,β₃ – измеренные углы.

Σβ_изм.= β₁=74˚02'13''+75˚50'40''+30˚07'10''=180˚00'03''

2. 
   Вычисляется сумма теоретических сумма углов для замкнутого теодолитного хода
   

Σ β_теор.=180∙(n-2),

где n – число вершин замкнутого теодолитного хода.

Σ β_теор.=180∙(3-2)= 180˚00'00''

3. 
   Вычисляется практическая угловая невязка теодолитного хода (f_β)
   

^fβ^{= Σβ}изм.^{- Σ β}теор. f_β=180˚00'03''-180˚00'00''=+00˚00'03''

4. 
   Вычисляется максимально допустимая угловая невязка (f_β^доп.)
   

β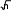
f ^доп.=±2∙t·

где t – точность теодолита.


β
f ^доп.=±2∙20''∙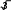
=±69''=±00˚01'09''

5. 
   
   β
   Если практическая угловая невязка f_βне превышает f ^доп., то она распределяется равномерно по измеренным углам с противоположным знаком путем введения поправки V и получаем исправленные углы β_испр.
   

V= -

f_{ ,}

n

^βиспр.^{= β}изм.^{+ V,}

V=- ⁰³// = -01''.

3

Значение исправленных углов теодолитного хода вносятся в графу 3 табл.

2.

6. 
   Выполняется контроль: сумма исправленных углов в замкнутом
   

теодолитном ходе должна быть равна Σ β_теор.

Σ β_испр.= Σ β_теор.= 180˚00'00''

Полученные суммы и величины из п. 1-6 обработки необходимо внести в ведомость подсчета вершин теодолитного хода через две строки после последней вершины (3) в соответствующие графы табл. 2.

7. 
   Вычисляются дирекционные углы сторон теодолитного хода. Дирекционный угол α_1-2 выдается преподавателем каждому студенту индивидуально. Остальные углы вычисляются по формулам:
   

^α2-3^{= α}1-2^{+180˚- β}2.исправ, ^α3-1^=α2-3^{+180˚- β}3.исправ.

Если вычисленный дирекционный угол получается больше 360˚, то

необходимо вычесть из него 360˚ и в дальнейшие вычисления подставлять уменьшенный угол.

8. 
   Выполняется проверка
   

^Α1-2^{= α}3-1^{+180˚- β}1.исправ.

9. 
   Вычисляются румбы сторон теодолитного хода по схеме (рисунок 13):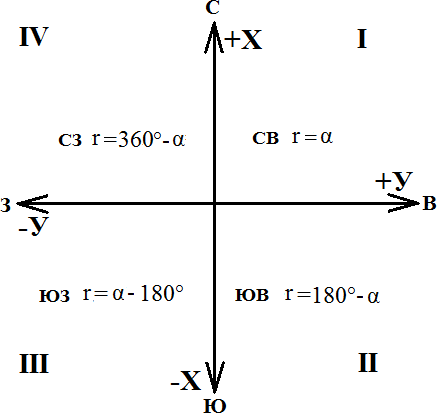
   

Рисунок 13Схема вычисления дирекционных углов и румбов сторон теодолитного хода

10. 
    Вычисляется периметр теодолитного хода
    

^P=D1-2^{+ D}2-3^{+ D}3-1

где D- длина стороны теодолитного хода.

P= 128,95+247,00+249,00=624,95 м.

Его необходимо записать в ведомость через 2 строки в графу 6.

11. 
    Вычисляются приращения координат по осям ΔX и ΔY:
    

ΔX=D∙cos α, ΔY= D∙sin α, ΔX_1-2= D_1-2∙cos α_1-2, ΔY_1-2= D_1-2∙sin α_1-2, ΔX_2-3= D_2-3∙cos α_2-3, ΔY_2-3= D_2-3∙sin α_2-3, ΔX_3-1= D_3-1∙cos α_3-1, ΔY_3-1= D_3-1∙sin α_3-1.

12. 
    Вычисляется сумма приращений координат
    

Σ ΔX= ΔX_1-2 +ΔX_2-3 +ΔX_3-1, Σ ΔY= ΔY_1-2 +ΔY_2-3 +ΔY_3-1.

13. 
    Теоретическая сумма приращений координат для замкнутого теодолитного хода должна равняться нулю
    

Σ ΔX_теор.= 0,

Σ ΔY_теор.= 0.

14. 
    Вычисляется практическая линейная невязка теодолитного хода по осям ОХ и ОY:
    

f_ΔХ= Σ ΔX – Σ ΔX_теор, f_ΔY= Σ ΔY – Σ ΔY_теор.

15. 
    Вычисляется абсолютная линейная невязка: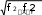
    

^fАБС.⁼

16. 
    Вычисляется относительная линейная невязка, причем она не должна превышать 1/2000 (для данных условий съемочных работ):
    

^fОТН.<sup>=

fАБС.</sup> >1/2000

Р

17. 
    Если выполняется условие пункта 16, то практическая линейная невязка распределяется по приращениям координат с противоположным знаком пропорционально длине стороны теодолитного хода. Для этого подсчитывается поправки по осям ОХ и ОY – V_ΔX и V_ΔY:
    

V_ΔX= -

^fХ_{ D}Р

, V_ΔY= -

^fY_{ D}Р _.

18. 
    Вычисляются исправленные приращения координат:
    

^ΔX1-2^{испр.= ΔX}1-2^{+ V}ΔX1-2^{, ΔY}1-2^{испр.= ΔY}1-2^{+ V}ΔY1-2

19. 
    Выполняется контроль:
    

ΣΔX^испр.= ΣΔX_теор.=0, ΣΔY^испр.= ΣΔY_теор.=0.

20. 
    Вычисляются координаты точек теодолитного хода. Координаты первой точки теодолитного хода известны и выдаются преподавателем. Координаты остальных точек вычисляются по формулам:
    

X₂=X₁+ ΔX_1-2^испр. ,Y₂=Y₁+ ΔY_1-2^испр., X₃=X₂+ ΔX_2-3^испр. ,Y₃=Y₂+ ΔY_2-3^испр..

21. 
    Выполняется контроль:
    

X₁=X₃+ ΔX_3-1^испр. Y₁=Y₃+ ΔY_3-1^испр.

Все полученные результаты вычислений заносятся в ведомость вычисления координат вершин теодолитного хода (табл. 2).

Таблица 2

Ведомость вычисления координат вершин теодолитного хода

№ Вер- шины	Внутренние углы								Дирекционные углы				Румбы сторон					Горизо нтальн ыепрол ожения сторон		Приращения координат													Координаты
	измеренные				исправленные
	˚	ˊ	ˊˊ	˚		ˊ	ˊˊ	˚		ˊ	ˊˊ	наз.		˚	ˊ	ˊˊ	м		вычисленные						исправленные
																			±		X	±		Y	±		X	±		Y		X			Y
1	2			3					4				5					6		7			8			9			10					11		12
1	74	2	15-2	74		2	13																									130,00			130,00
								10		15	27	СВ		10	15	27	128,95		+		-0,01 126,89	+		-0,02 22,96	+		126,88	+		22,94
2	75	50	40-2	75		50	38																									256,88			152,94
								114		24	49	ЮВ		65	35	11	247,00		-		-0,02 102,09	+		-0,04 224,91	-		102,11	+		224,87
3	30	7	10-1	30		7	9																									154,77			377,81
								264		17	40	ЮЗ		84	17	40	249,00		-		-0,02 24,75	-		-0,04 247,77	-		24,77	-		247,81
																																130,00			130,00
∑βпр	180	00	05
∑βтеор.	180	00	00														Р=624,9 5				∑ΔX=+ 0,05			∑ΔY=+ 0,10			∑ΔX=0			∑ΔY=0
fβ	+00	00	05																		fабс.=0,11
доп fβ	±00	01	09																		fотн.=0,0002=1/5000≤1/2 000
∑βиспр.	180	00	00