Управление проектами - И.И. Мазур. Учебное пособие 2е издание Под общей редакцией профессора и. и. Мазура Допущено
 Скачать 8.48 Mb. Скачать 8.48 Mb.
|
|
Экспертный анализ рисков Экспертный анализ рисков применяют на начальных этапах работы с проектом в случае, если объем исходной информации является недостаточным для количественной оценки эффективности (погрешность результатов превышает 30%) и рисков проекта. Достоинствами экспертного анализа рисков являются: отсутствие необходимости в точных исходных данных и дорогостоящих программных средствах, возможность проводить оценку до расчета эффективности проекта, а также простота расчетов. К основным недостаткам следует отнести: трудность в привлечении независимых экспертов и субъективность оценок. Эксперты, привлекаемые для оценки рисков, должны:
Алгоритм экспертного анализа рисков следующий:
Анализ показателей предельного уровня Показатели предельного уровня характеризуют степень устойчивости проекта по отношению к возможным изменениям условий его реализации. Предельным значением параметра для t-oro года является такое значение, при котором чистая прибыль от проекта равна нулю. Основным показателем этой группы является точка безубыточности (ТБ) — уровень физического объема продаж на протяжении расчетного периода времени, при котором выручка от реализации продукции совпадает с издержками производства. Для подтверждения устойчивости проекта необходимо, чтобы значение точки безубыточности было меньше значений номинальных объемов производства и продаж. Чем дальше от них значение точки безубыточности (в процентном отношении), тем устойчивее проект. Проект обычно признается устойчивым, если значение точки безубыточности не превышает 75% от номинального объема производства. Точка безубыточности определяется по формуле: где Зс — постоянные затраты, размер которых напрямую не связан с объемом производства продукции (руб.), Ц — цена за единицу продукции (руб.), 3v — переменные затраты, величина которых изменяется с изменением объема производства продукции (руб./ед.). Распределение затрат на постоянные и переменные, укрупнено показанное в табл. 21.2.5, является приблизительным и может изменяться в зависимости от конкретных условий: системы начисления заработной платы, сбыта продукции и других особенностей производства. Ограничения, которые должны соблюдаться при расчете точки безубыточности:
Таблица 21.2.5 Постоянные и переменные затраты на проект
Уровень резерва прибыльности (РП) как доли от планируемого объема продаж (ОП) определяется по формуле: РП = (ОП - ТБ)/ОП. Расчет точки безубыточности может быть проиллюстрирован с помощью графика, приведенного на рис. 21.2.5. Показатель точки безубыточности позволяет определить:
Показатель точки безубыточности следует использовать при:
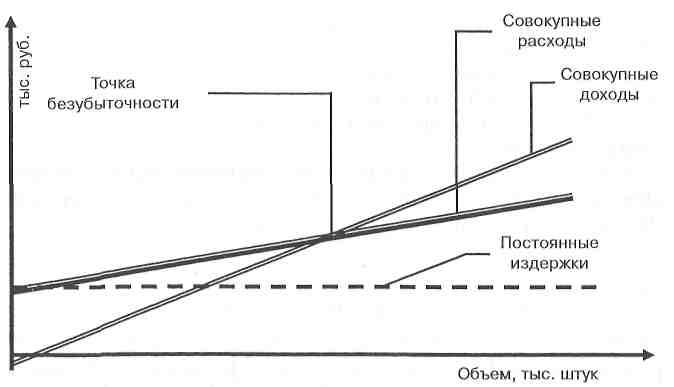 Рис. 21.2.5. Графическое представление точки безубыточности Расчет точки безубыточности усложняется при оценке проекта, результатом которого является выпуск нескольких видов продукции. Пример расчета точки безубыточности для этого случая приведен в табл. 21.2.6. Таблица 21.2.6 Расчет точки безубыточности для предприятия, выпускающего три вида продукции
Анализ чувствительности проекта Задача количественного анализа состоит в численном измерении влияния изменений рискованных факторов на эффективность проекта. Общая схема анализа чувствительности проекта состоит в следующем. Анализ чувствительности (уязвимости) происходит при «последовательно-единичном» изменении каждой переменной: только одна из переменных меняет свое значение (например, на 10%), на основе чего пересчитывается новая величина используемого критерия (например, ЧДЦ). После этого оценивается процентное изменение критерия по отношению к базисному случаю и рассчитывается показатель чувствительности, представляющий собой отношение процентного изменения критерия к изменению значения переменной на один процент (так называемая эластичность изменения показателя). Таким же образом исчисляются показатели чувствительности по каждой из остальных переменных. Затем на основании этих расчетов происходит экспертное ранжирование переменных по степени важности (например, очень высокая, средняя, невысокая) и экспертная оценка прогнозируемоcти (предсказуемости) значений переменных (например, высокая, средняя, низкая). Далее эксперт может построить так называемую «матрицу чувствительности», позволяющую выделить наименее и наиболее рискованные для проекта переменные (показатели) (табл. 21.2.7). Приведем пример анализа чувствительности инвестиционного проекта, данные условные. Таблица 21.2.7 Определение рейтинга факторов проекта, проверяемых на риски
Таблица 21.2.8 Показатели чувствительности и прогнозируемости переменных в проекте
Таблица 21.2.9. Матрица чувствительности и предсказуемости
Табл. 21.2.8 называется матрицей чувствительности, степени которой отражены в сказуемом таблицы (по горизонтали) и предсказуемости; степени которой представлены в подлежащем (по вертикали). На основе результатов анализа каждый фактор займет свое соответствующее место в поле матрицы (табл. 21.2.9). В соответствии с экспертным разбиением чувствительности и предсказуемости по их степеням матрица содержит девять элементов, которые можно распределить по зонам. Попадание фактора в определенную зону будет означать конкретную рекомендацию для принятия решения о дальнейшей с ним работе по анализу рисков. Итак, первая зона (I) — левый верхний угол матрицы — зона дальнейшего анализа попавших в нее факторов, так как к их изменению наиболее чувствительна ЧДЦ проекта и они обладают наименьшей прогнозируемостью. Вторая зона (II) совпадает с элементами побочной диагонали матрицы и требует пристального внимания к происходящим изменениям расположенных в ней факторов (в частности, для этого и производился расчет критических значений каждого фактора). Наконец, третья зона (III), правый нижний угол таблицы, — зона наибольшего благополучия: в ней находятся факторы, которые при всех прочих предположениях и расчетах являются наименее рискованными и не подлежат дальнейшему рассмотрению. В соответствии с данными табл. 21.2.6 и 21.2.7 распределение факторов по зонам в нашем условном примере следующее:
Отметим, что, несмотря на все свои преимущества — теоретическую прозрачность, простоту расчетов, экономико-математическую естественность результатов и наглядность их толкования (именно эти критерии и лежат в основе его широкой практической применимости), метод анализа чувствительности имеет существенные недостатки. Первый и основной из них — его однофакторность, т.е. ориентация на изменения только одного фактора проекта, что приводит к недоучету возможной связи между отдельными факторами или к недоучету их корреляции. Анализ чувствительности проекта позволяет оценить, как изменяются результирующие показатели реализации проекта при различных значениях заданных переменных, необходимых для расчета. Этот вид анализа позволяет определить наиболее критические переменные, которые в наибольшей степени могут повлиять на осуществимость и эффективность проекта. В качестве варьируемых исходных переменных принимают:
В качестве результирующих показателей реализации проекта могут выступать:
При относительном анализе чувствительности сравнивается относительное влияние исходных переменных (при их изменении на фиксированную величину, например, на 10%) на результирующие показатели проекта. Этот анализ позволяет определить наиболее существенные для проекта исходные переменные; их изменение должно контролироваться в первую очередь. Абсолютный анализ чувствительности позволяет определить численное отклонение результирующих показателей при изменении значений исходных переменных. Значения переменных, соответствующие нулевым значениям результирующих показателей, соответствуют рассмотренным выше показателям предельного уровня. Результаты анализа чувствительности приводятся в табличной или графической формах. Последняя является более наглядной (рис. 21.2.6) и должна применяться в презентационных целях. Анализ сценариев развития проекта Анализ сценариев развития проекта позволяет оценить влияние на проект возможного одновременного изменения нескольких переменных через вероятность каждого сценария. Этот вид анализа может выполняться как с помощью электронных таблиц (например, Microsoft Excel версии не ниже 4.0), так и с применением специальных компьютерных программ, позволяющих использовать методы имитационного моделирования. В первом случае формируются 3—5 сценариев развития проекта (табл. 21.2.10). Каждому сценарию должны соответствовать:
В результате расчета определяются средние (с учетом вероятности наступления каждого сценария) значения результирующих показателей. Таблица 21.2.10 Сценарии развития проекта
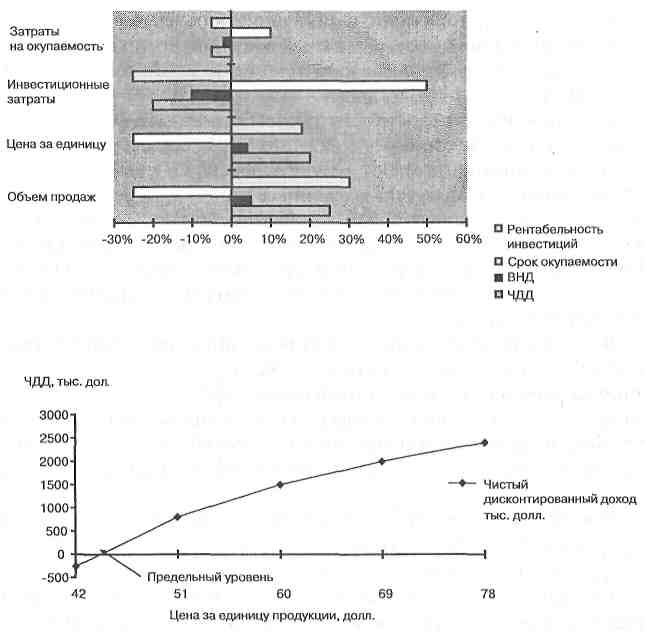 Рис. 21.2.6. Формы представления результатов относительного и абсолютного анализа чувствительности проекта Метод построения дерева решений проекта В случае небольшого числа переменных и возможных сценариев развития проекта для анализа рисков можно также воспользоваться методом дерева решений . Преимущество данного метода — в его наглядности. Последовательность сбора данных для построения дерева решений при анализе рисков включает следующие шаги:
На основании полученных данных строится дерево решений. Его узлы представляют собой ключевые события, а стрелки, соединяющие узлы, — проводимые работы по реализации проекта. Кроме того, на дереве решений приводится информация относительно времени, стоимости работ и вероятности принятия того или иного решения. В результате построения дерева решений определяется вероятность каждого сценария развития проекта, эффективность по каждому сценарию, а также интегральная эффективность проекта. Положительная величина показателя эффективности проекта (например, чистого дисконтированного дохода) указывает на приемлемую степень рисков, связанного с осуществлением проекта. Пример. Компания «УУУ» собирается инвестировать средства в производство роботов для использования в космических исследованиях. Инвестиции в данный проект производятся в три этапа. 1-йэтап. В начальный момент времени t=0 необходимо потратить $500 тыс. долл. на проведение маркетингового исследования рынка. 2-йэтап. Если в результате исследования будет выяснено, что потенциал рынка достаточно высок, то компания инвестирует еще $1,000 тыс. долл. на разработку и создание опытных образцов робота. Опытные образцы должны быть предложены к рассмотрению инженерам в центре космических исследований, которые решают вопрос о размещении заказа у данной компании. 3-йэтап. Если реакция инженеров благоприятная, то в момент времени t=2 компания начинает строительство нового предприятия по производству данного робота. Строительство такого предприятия требует затрат в $10,000 тыс. долл. Если данная стадия будет реализована, то по оценкам менеджеров проект будет генерировать притоки наличности в течение четырех лет. Величина этих потоков наличности будет зависеть от того, насколько хорошо этот робот будет принят на рынке. Для анализа именно таких многостадийных решений чаще всего используется метод дерева решений (рис. 21.2.7). Единица измерения — тыс. долл. 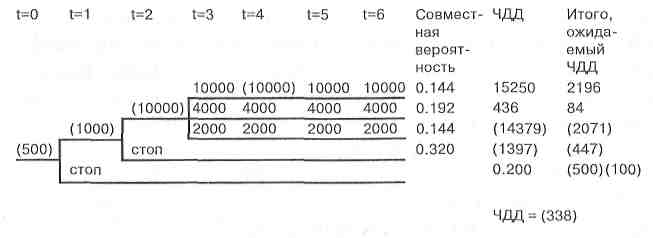 Рис. 21.2.7. Дерево решений проекта В этом примере мы предполагаем, что очередное решение об инвестировании принимается компанией в конце каждого года. Каждое «разветвление» обозначает точку принятия решения, либо очередной этап. Число в круглых скобках, записанное слева от точки принятия решения, представляет собой чистые инвестиции. В интервале с третьего по шестой годы (с t=3 пo t=6) показаны притоки наличности, которые генерируются проектом. Например, если компания решает реализовывать проект в точке t=0, то она должна потратить 500 тыс. долл на проведение маркетингового исследования. Менеджеры компании оценивают вероятность получения благоприятного результата в 80%, и вероятность получения неблагоприятного результата в 20%. Если проект будет остановлен на этой стадии, то издержки компании составят 500 тыс. долл. Если по результатам маркетингового исследования компания приходит к оптимистическому заключению о потенциале рынка, то в момент времени t=1 необходимо потратить еще 1,000 тыс.долл. на изготовление экспериментального варианта робота. Менеджеры компании оценивают вероятность положительного исхода в 60%, а вероятность отрицательного исхода в 40%. Если инженеров центра космических исследований устраивает данная модель робота, тогда компания в момент времени t=2 должна инвестировать 10 000 тыс. долл. для постройки завода и начала производства. Менеджеры компании оценивают вероятность того, что в центре космических исследований воспримут такую модель благожелательно в 60% и вероятность противоположного исхода в 40% (что приведет к прекращению реализации проекта). Если компания приступает к производству робота, то операционные потоки наличности в течение четырехлетнего срока жизни проекта будут зависеть от того, насколько хорошо продукт будет «принят» рынком. Вероятность того, что продукт будет хорошо «принят» рынком составляет 30% и в этом случае чистые притоки наличности должны составлять около 10 000 тыс. долл. в год. Вероятность того, что притоки наличности будут составлять около 4 000 тыс. долл. и 2 000 тыс. долл. в год, равна 40% и 30% соответственно. Эти ожидаемые потоки наличности показаны на нашем рисунке с третьего года по шестой. Совместная вероятность, подсчитанная на выходе данной схемы, характеризует ожидаемую вероятность получения каждого результата. Предположим, что ставка цены капитала компании при реализации данного проекта составляет 11,5%, и по оценкам финансовых менеджеров компании реализация данного проекта имеет риски, равные рискам реализации типичного «среднего» проекта компании. Затем, умножая полученные значения чистой приведенной стоимости на соответствующие значения совместной вероятности, мы получим ожидаемую чистую приведенную стоимость инвестиционного проекта. Поскольку ожидаемая чистая приведенная стоимость проекта получилась отрицательной, то компания должна отвергнуть этот инвестиционный проект. Однако на самом деле, вывод не так однозначен. Необходимо также учесть возможность отказа компании от реализации данного проекта на определенном этапе или стадии, что приводит к существенному изменению одной из ветвей дерева решений. Издержки отказа от реализации проекта значительно сокращаются, если компания имеет альтернативу для использования активов проекта. Если бы в нашем примере, компания могла бы использовать оборудование для производства принципиально иного вида роботов, тогда бы проект по производству роботов для космических нужд мог быть ликвидирован с большей легкостью, следовательно, риски реализации проекта были бы меньше. Имитационное моделирование рисков на базе метода Монте-Карло Анализ рисков с использованием метода моделирования Монте-Карло представляет собой сочетание методов анализа чувствительности и анализа сценариев. Это достаточно сложная методика, имеющая под собой, как правило, компьютерную реализацию. Результатом такого анализа выступает распределение вероятностей возможных результатов проекта. Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию) получить распределение доходности проекта. При формировании сценариев с использованием методов имитационного моделирования применяется следующая последовательность действий:
Анализ значений результирующих показателей при сформированных сценариях позволяет оценить возможный интервал их изменения при различных условиях реализации проекта. Вероятностные характеристики используются для:
На рис. 21.2.8 представлена схема работы с имитационной моделью. Применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master), в то время, как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.  Рис. 21.2.8. Схема имитационного моделирования рисков проекта Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения чистой дисконтированного дохода ЧДД<0). Несмотря на свои достоинства, метод Монте-Карло не распространен и не используется слишком широко в бизнесе. Одна из главных причин этого — неопределенность функций распределения переменных, которые используются при расчетах. Другая проблема, которая возникает как при использовании метода сценариев, так и при использовании метода Монте-Карло, состоит в том, что применение обоих методов не дает однозначного ответа на вопрос о том, следует ли все же реализовы-вать данный проект или следует отвергнуть его, поэтому, как правило, используется целый комплекс методов анализа рисков проекта для окончательной оценки. Общая результативность анализа проектных рисков может быть оценена следующим образом: Преимущества методов 1.Совершенствует уровень принятия решений по малоприбыльным проектам. Проект с малым значением ЧДД может быть принят, в случае если анализ рисков установит, что шансы получить удовлетворительный доход превосходят вероятность неприемлемых убытков. 2.Помогает идентифицировать производственные возможности. Анализ рисков помогает сэкономить деньги, потраченные на получение информации, издержки на получение которой превосходят издержки неопределенности. 3.Освещает сектора проекта, требующие дальнейшего исследования и управляет сбором информации. 4. Выявляет слабые места проекта и дает возможность внести поправки. 5. Предполагает неопределенность и возможные отклонения факторов от базовых уровней. В связи с тем, что присвоение распределений и границ варьирования переменных несет оттенок субъективизма, необходимо критически подходить даже к результатам анализа рисков. Сложности применения методов
21.3. Методы снижения рисков Все методы, позволяющие минимизировать проектные риски можно разделить на три группы: 1. Диверсификация, или распределение рисков (распределение усилий предприятия между видами деятельности, результаты которых непосредственно не связаны между собой), позволяющая распределить риски между участниками проекта. Распределение проектным рисков между его участниками является эффективным способом его снижения Теория надежности показывает, что с увеличением количества параллельных звеньев в системе вероятность отказа в ней снижается пропорционально количеству таких звеньев. Поэтому распределение рисков между участниками повышает надежность достижения результата. Логичнее всего при этом сделать ответственным за конкретный вид риска того из его участников, который обладает возможностью точнее и качественнее рассчитывать и контролировать данный риск. Распределение рисков оформляется при разработке финансового плана проекта и контрактных документов. Распределение рисков фактически реализуется в процессе подготовки плана проекта и контрактных документов. Следует иметь в виду, что повышение рисков у одного из участников должно сопровождаться адекватным изменением в распределении доходов от проекта. Поэтому при переговорах необходимо:
2. Резервирование средств на покрытие непредвиденных расходов представляет собой способ борьбы с риском, предусматривающий установление соотношения между потенциальными рисками, влияющими на стоимость проекта, и размером расходов, необходимых для преодоления сбоев в выполнении проекта. Величина резерва должна быть равна или превышать величину колебания параметров системы во времени. В этом случае затраты на резервы должны быть всегда ниже издержек (потерь), связанных с восстановлением отказа. Зарубежный опыт допускает увеличение стоимости проекта от 7 до 12% за счет резервирования средств на форс-мажор. Резервирование средств предусматривает установление соотношения между потенциальными рисками, изменяющими стоимость проекта, и размером расходов, связанных с преодолением нарушений в ходе его реализации. Российские эксперты рекомендуют следующие примерные нормы непредвиденных расходов (табл. 21.3.1). Таблица 21.3.1. Нормы резервирования средств на непредвиденные расходы
Минимизация рисков всегда увеличивает проектные затраты, но зато увеличивает и проектную прибыль. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
