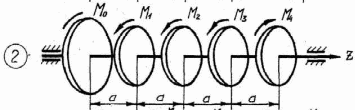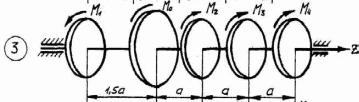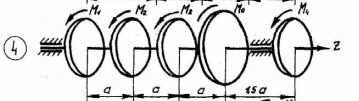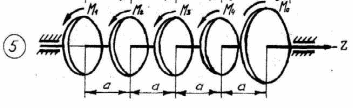ЗАДАНИЕ № 2
РАСЧЕТ НА ПРОЧНОСТЬ СТУПЕНЧАТОГО БРУСА КРУГЛОГО
СЕЧЕНИЯ НА ОСЕВОЕ РАСТЯЖЕНИЕ - СЖАТИЕ
Методические рекомендации к решению задач
Приступая к решению задач необходимо рассмотреть следующие вопросы из теоретического материала данной темы:
основные понятия - деформации, напряжения, внешние и
внутренние силы;
метод сечений;
продольная сила и напряжение в поперечных сечениях бруса;
допускаемые напряжения;
расчеты на прочность.
Вопросы для самопроверки
1 Какие деформации называются упругими?
2 Какие деформации называются остаточными (пластическими)?
3 Что называется напряжением в точке в данном сечении?
4 Какое напряжение называется нормальным?
5 Какое напряжение называется касательным?
6 В чем заключается сущность метода сечений?
7 Что называется коэффициентом запаса прочности?
8 Как формулируется условие прочности?
Задачи на осевое растяжение – сжатие рекомендуется решать в
следующем порядке:
Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.
Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N), построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
14
План решения задачи
1 Вычертить схему нагружения бруса.
2 Построить эпюру продольных сил.
3 Определить из условия прочности диаметры на всех участках бруса. Округлить полученные значения до стандартных размеров по ГОСТ 6636- 69. Дать эскиз ступенчатого бруса с указанием диаметров на каждом участке (материал бруса-Ст.З).
4 Построить эпюру напряжений.
5 Определить абсолютную деформаций по его длине
(длина бруса l=2м.). Таблица 2.1 Рисунок 2.2
Таблица 2.1- Числовые данные
Номер
варианта
|
Силы, кН
|
Размеры, м
|
Отношение
диаметров
|
F1
|
F2
|
F3
|
а
|
b
|
0
|
5,0
|
30,0
|
50,0
|
0,2
|
0,5
|
0,3
|
1
|
10,0
|
40,0
|
20,0
|
0,4
|
0,6
|
0,4
|
2
|
20,0
|
10,0
|
60,0
|
0,6
|
1,0
|
0,7
|
3
|
15,0
|
20,0
|
40,0
|
0,3
|
1,2
|
0,8
|
4
|
30,0
|
25,0
|
20,0
|
0,35
|
1,5
|
0,9
|
5
|
25,0
|
50,0
|
30,0
|
0,5
|
1,0
|
0,5
|
6
|
40,0
|
45,0
|
50,0
|
0,4
|
0,8
|
0,6
|
7
|
20,0
|
30,0
|
50,0
|
0,25
|
1,0
|
0,7
|
8
|
50,0
|
30,0
|
40,0
|
0,6
|
1,4
|
0,4
|
9
|
60,0
|
20,0
|
50,0
|
0,8
|
1,6
|
0,8
|
15
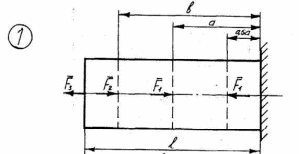
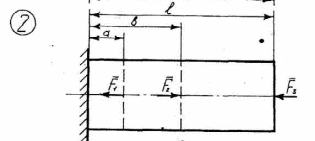
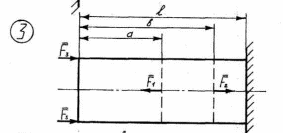
Рисунок 2.1 – Схемы нагружения стержней
16
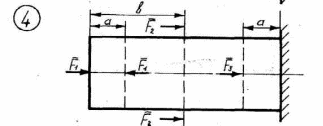
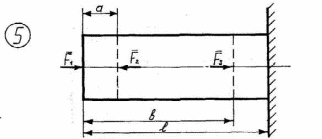
Рисунок 2.1 – Продолжение
17
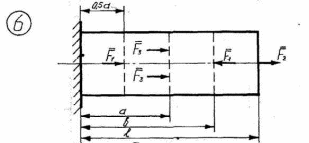

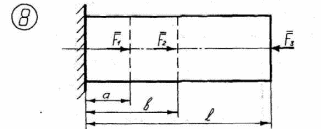
Рисунок 2.1 – Продолжение
18
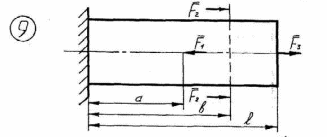
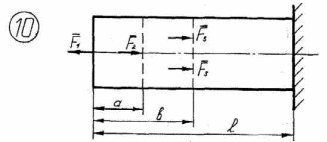
Рисунок 2.1 – Продолжение
19
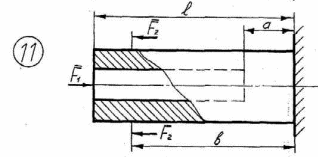
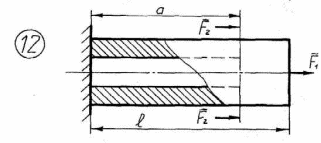
Рисунок 2.1 – Продолжение
20
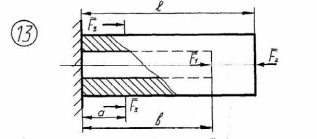
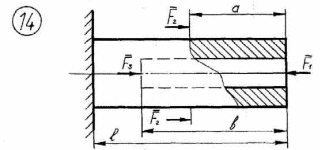
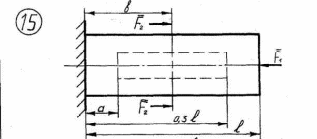
Рисунок 2.1 – Продолжение
21
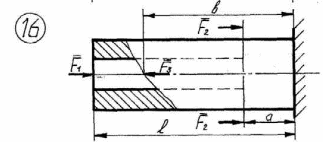
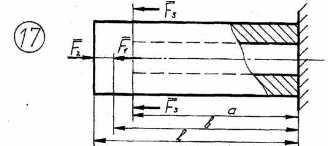
Рисунок 2.1 – Продолжение
22
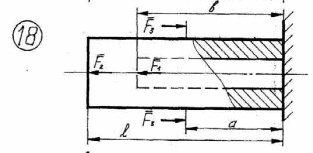
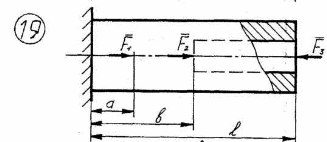
Рисунок 2.1 – Продолжение
23
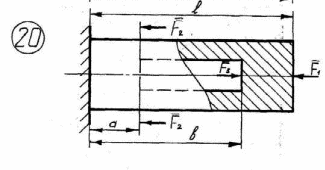
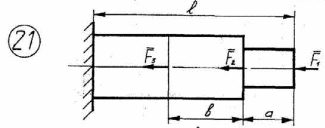
Рисунок 2.1 – Продолжение
24
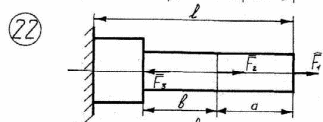
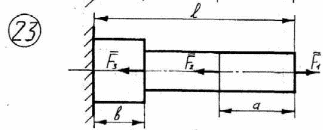
Рисунок 2.1 – Продолжение
25

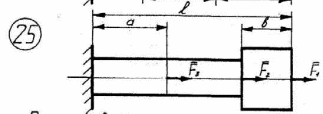
Рисунок 2.1 – Окончание
26
ЗАДАНИЕ № 3
Р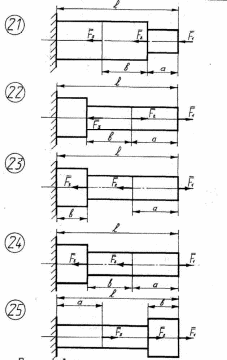 АСЧЕТ ВАЛОВ НА КРУЧЕНИЕ АСЧЕТ ВАЛОВ НА КРУЧЕНИЕ
Методические рекомендации к решению задач
Приступая к решению задач, необходимо рассмотреть следующие вопросы из теоретического материала данной темы.
1Основные понятия. Деформация кручения. Скручивающие моменты. Метод сечения для определения крутящих моментов.
2Расчет бруса круглого поперечного сечения на жесткость и прочность при кручении.
3Вычисление моментов инерции, сечений простой формы.
4Главные моменты инерции, главные оси инерции.
Вопросы для самопроверки
1 Какие напряжения возникают в поперечном сечении круглого стержня при кручении?
2 Как находится величина в произвольной точке поперечного сечения?
3 Возникают ли при кручении нормальные напряжения?
4 Чему равен полярный момент инерции круглого сечения?
5 Что называется моментом сопротивления при кручении? В каких единицах
он измеряется?
6 Чему равен момент сопротивления кольцевого сечения? Почему нельзя сказать, что он равен разности моментов сопротивления наружного и внутреннего кругов?
7 Как вычисляется момент, передаваемый шкивом, по мощности и числу
оборотов?
8 Как находится величина угла закручивания?
9 Как производится расчет вала на прочность?
10 Как производится расчет вала на жесткость?
11 Как находятся максимальные напряжения при кручении стержня
прямоугольного сечения?
Задачи на деформацию кручения необходимо решать в следующей последовательности:
1 Определить внешние скручивающие моменты по формуле
М=Р/ω , где Р-мощность, ω - угловая скорость.
2 Определить уравновешивающий момент, используя уравнение равновесия Σ Мi =0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.
3 Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.
27
4 Для участка вала, в котором возникает небольшой крутящий момент, определить диаметр вала круглого или кольцевого сечения из условия прочности и жесткости. Для кольцевого сечения вала принять соотношение диаметров
с = d0/d, где d0 - внутренний диаметр кольца; d - наружный диаметр кольца.
План решения задачи
1 Вычертить схему вала.
2 Определить из условия равновесия вала мощность Р0, пренебрегая трением в подшипниках.
3 Определить скручивающие моменты, передаваемые каждым шкивом.
4 Построить эпюру крутящих моментов.
5 Определить диаметр вала на каждом участке из условия прочности; округлить полученные величины до стандартных размеров в большую сторону по ГОСТ 6636-69. Дать эскиз ступенчатого вала с указанием диаметров. (Материал вала-Ст.45.)
6 Определить величину yгла закручивания для всего вала, принимая
за неподвижное сечение один из концов вала (а=1м).
7. Построить эпюру углов закручивания, (а=1м).
Диаметры валов согласно ГОСТ 6636
69 должны соответствовать ряду предпочтительных чисел: 5,0; 6,0; 7,5; 8,0; 8,5; 9,0; 9,5; 10; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50.
Таблица 3.1 Рисунок 3.1
Таблица 3.1- Числовые данные
Номер
варианта
|
Мощности, передаваемые шкивами, кВт
|
Скорость вращения
вала , с-1
|
Р1
|
Р2
|
Р3
|
Р4
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
4,0
|
1
|
0,2
|
0,3
|
0,4
|
0,1
|
5,0
|
2
|
0,3
|
0,4
|
0,1
|
0,2
|
6,0
|
3
|
0,4
|
0,3
|
0,2
|
0,1
|
7,0
|
4
|
1,0
|
2,0
|
3,0
|
4,0
|
8,0
|
5
|
2,0
|
3,0
|
4,0
|
5,0
|
9,0
|
6
|
3,0
|
4,0
|
1,0
|
2,0
|
10
|
7
|
4,0
|
2,0
|
5,0
|
3,0
|
15
|
8
|
6,0
|
7,0
|
8,0
|
10,0
|
100
|
9
|
10,0
|
20,0
|
30,0
|
40,0
|
200
|
28

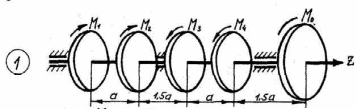
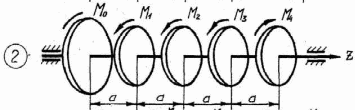
Рисунок 3.1 – Схема нагружения валов.
29

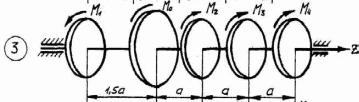
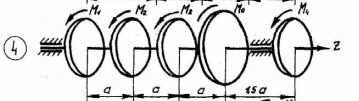
Рисунок 3.1 – Продолжение
30

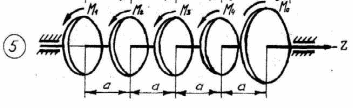
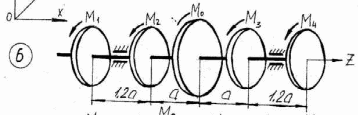
Рисунок 3.1 – Продолжение
31


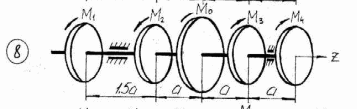
Рисунок 3.1 – Продолжение
32

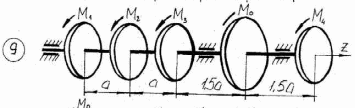
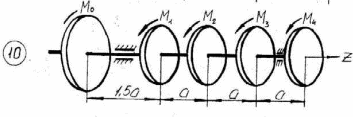
Рисунок 3.1 – Продолжение
33

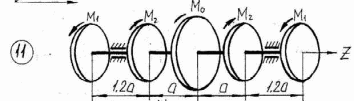
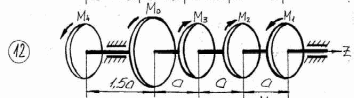
Рисунок 3.1 – Продолжение
34
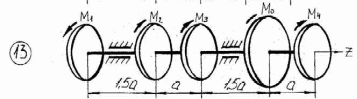
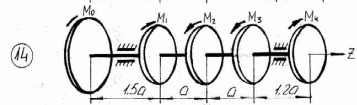
Рисунок 3.1 – Продолжение
35

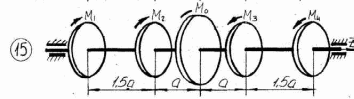
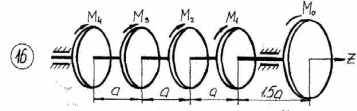
Рисунок 3.1 – Продолжение
36

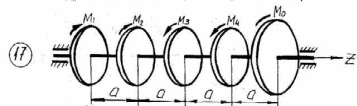
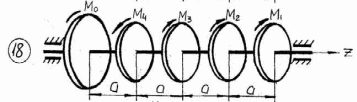
Рисунок 3.1 – Продолжение
37

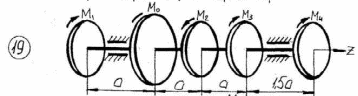
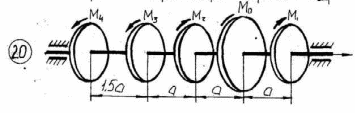
Рисунок 3.1 – Продолжение
38

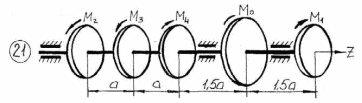
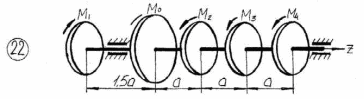
Рисунок 3.1 – Продолжение
39

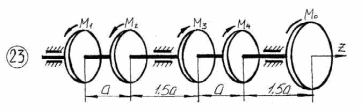
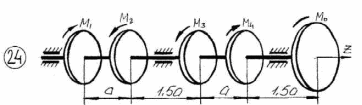
Рисунок 3.1 – Продолжение
40

Рисунок 3.1 – Окончание
41 |
 Скачать 1.6 Mb.
Скачать 1.6 Mb.