Курсовая работа по электрическим машинам. курсовая 19. Утверждаю заведующий кафедрой (число, месяц, год) задание 19
 Скачать 163.99 Kb. Скачать 163.99 Kb.
|
Удельная тепловая нагрузка: Вт/м2: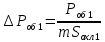 (5.4.1) (5.4.1)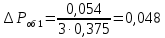 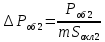 (5.4.2) (5.4.2)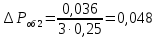 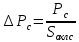 (5.4.3) (5.4.3)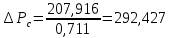 где Sохл1, Sохл2, Sохл.с– соответственно поверхности охлаждения обмоток ВН, НН и стали сердечника, м2: Sохл1 = 2КзакДср1hоб (5.4.4) Sохл1 = 2∙0,8∙3,14∙0,213∙0,351=0,375 Sохл2 = 2КзакДср2hоб (5.4.5) Sохл2 = 2∙0,8∙3,14∙0,142∙0,351=0,25 Sохл.с = m1КзакДlст + 2Даlа (5.4.6) Sохл с = 3∙0,8∙3,14∙0,11∙0,351+2∙3,14∙0,11∙0,61=0,711 где Да и lа соответственно диаметр и полная длина ярма, м; hоб – высота обмотки, м; Кзак – коэффициент закрытия, учитывающий уменьшение поверхности охлаждения обмоток и стали сердечника за счет различных прокладок Кзак≈ 0,8. 6. Расчет эксплуатационных характеристик трансформатора 6.1 Параметры схемы замещения трансформатора определяем следующим образом Находим полное сопротивление короткого замыкания и его составляющие, Ом: 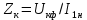 (6.1.1) (6.1.1)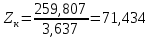 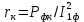 (6.1.2) (6.1.2)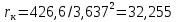 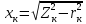 (6.1.3) (6.1.3)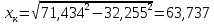 где Uк.ф – фазное значение напряжения короткого замыкания, В; I1н – номинальный ток первичной обмотки трансформатора, А. Фазное значение напряжения короткого замыкания, В: Uфк= U1ф∙ Uк/100 (6.1.4) Uфк= 5773,5 ∙4,5/100=259,807 Считая сопротивление первичной обмотки и приведенное сопротивление вторичной обмотки примерно одинаковыми, определяют их по формулам, Ом: 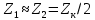 (6.1.5) (6.1.5)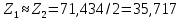 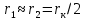 (6.1.6) (6.1.6)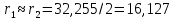 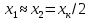 (6.1.7) (6.1.7)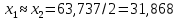 Сопротивление холостого хода и его составляющие находим из соотношений, кОм: 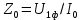 (6.1.8) (6.1.8)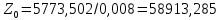 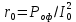 (6.1.9) (6.1.9)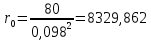 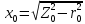 (6.1.10) (6.1.10)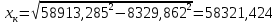 где U1ф – фазное напряжение первичной обмотки; 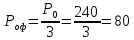 - потери холостого хода на фазу, Вт;I0- ток холостого хода, который определяется по формуле, А: - потери холостого хода на фазу, Вт;I0- ток холостого хода, который определяется по формуле, А:I0= (I0%∙ Iф)/100 (6.1.11) I0= (3,637∙2,7)/100=0,098 Сопротивление намагничивающего контура и его составляющие находят из соотношений, Ом: Zm = Z0 – Z1 (6.1.12) Zm = 58913,285 –35,717=58877,568 хm = x0 – x1 (6.1.13) хm = 58321,424-31,868=58289,556 rm = r0 –r1 (6.1.14) rm = 8329,862-16,127=8313,735 Т-образная схема замещения трансформатора приведена на рисунке 2. 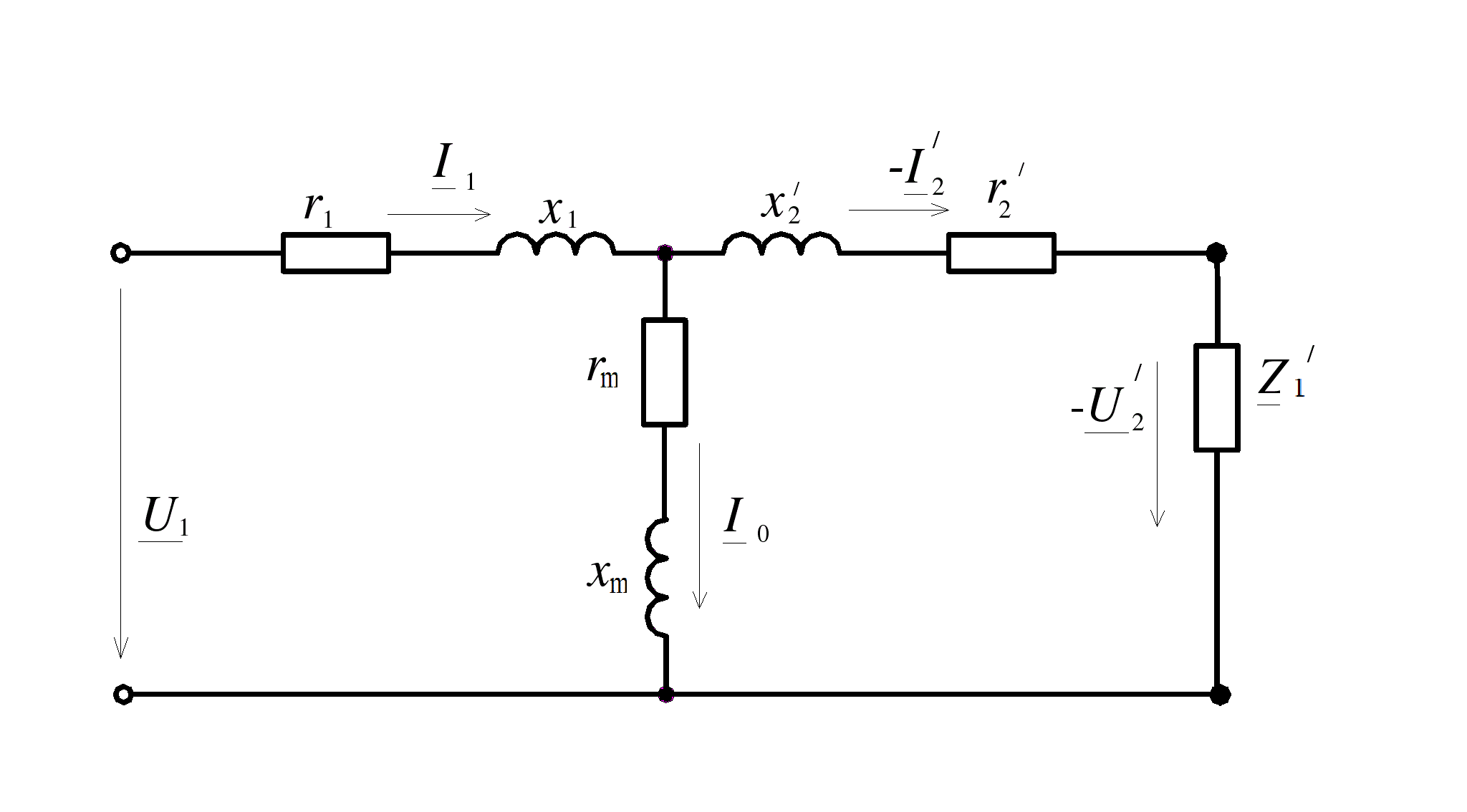 Рисунок 2. Т-образная схема замещения трансформатора 6.2 Векторная диаграмма Векторную диаграмму трансформатора строим для одной фазы при номинальной нагрузке и cosφ2 = 0,8 (отстающий ток) по известному току нагрузки, вторичному напряжению и углу сдвига между ними. Векторная диаграмма строится для фазных величин токов и напряжений в такой последовательности: Проводим вертикальный вектор 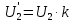 (6.2.1) (6.2.1)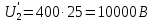 где k - коэффициент трансформации трансформатора (k=25). Под углом φ2=arccos(0,8) к 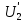 проводим вектор тока проводим вектор тока 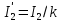 (6.2.2) (6.2.2)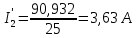 На основании уравнения трансформатора строим вектор ЭДС: 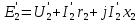 (6.2.3) (6.2.3)Перпендикулярно к вектору 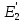 проводим вектор магнитного потока Фm произвольной длины. проводим вектор магнитного потока Фm произвольной длины.Строим на векторе Фm векторы Ixp и Ixa и получаем вектор тока холостого тока Ix. По уравнению I1=I0-I2 строим вектор первичного тока I1. На основании уравнения трансформатора 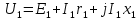 (6.2.4) (6.2.4)Строим вектор первичного напряжения U1 (E1=E2). Векторная диаграмма приведена на рисунке 4. 6.3 Зависимость изменения вторичного напряжения трансформатора от угла сдвига фаз между напряжением и током ΔU = β(Uкаcosφ2 + Uкрsinφ2) (6.3.1) ΔU = 1(2,57∙cos90 + 4,1∙sin90)=4,1 где β=1 – степень нагрузки трансформатора; Uка , Uкр – соответственно активная и реактивная составляющие напряжения короткого замыкания, %. Зависимость ΔU = f(φ2) рассчитываем для номинальной нагрузки при изменении φ2 в пределах от +900 до –900. Результаты расчета заносим в таблицу 1. Таблица 1. Зависимость ΔU = f(φ2)
Графическая зависимость ΔU = f(φ2) приведена на рисунке 5.6.4 Внешняя характеристика трансформатора Внешняя характеристика трансформатора – это зависимость вторичногонапряжения от степени нагрузки трансформатора при постоянных первичном напряжении, частоте и cosφ2. В работе рассчитываем внешние характеристики для cosφ2 = 1 и 0,6 при φ2> 0 и φ2< 0 и изменении нагрузки трансформатора от холостого хода до 1,5 номинальной. Для построения внешних характеристик рассчитываем по 5-6 точек для каждой характеристики. Значение вторичного напряжения в процентах определяем следующим образом, %: U2% = 100 – ΔU (6.4.1) U2% = 100 – 0=100 ΔU = 0·(2,57∙cos(0) + 4,1∙sin(0))=0 где ΔU – изменение вторичного напряжения трансформатора, которое определяется по выражению (6.3.1). Результаты расчета сводим в таблицу 2. Таблица 2. Внешняя характеристика трансформатора
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
