Курс на Си. Подбельский. Курс программирования на Си. В., Фомин С. С. Курс программирования на языке Си Учебник

• Название: В., Фомин С. С. Курс программирования на языке Си Учебник
• Анкор: Курс на Си
• Дата: 18.02.2023
• Размер: 1.57 Mb.
• Имя файла: Подбельский. Курс программирования на Си.docx
• Тип: Учебник; #943863
• страница: 6 из 42

. (точка) - прямой выбор (выделение) компонента структу­рированного объекта, например объединения или структуры (ранг 1). Формат применения операции:

имя_структурированного_объекта . имя_компонента

• 
  -> - косвенный выбор (выделение) компонента структури­рованного объекта, адресуемого указателем (ранг 1). При ис­пользовании операции требуется, чтобы с объектом был свя­зан указатель (указателям посвящена глава 4). В этом случае формат применения операции имеет вид: указатель_на_структурированный_объект -> имя_компонента
  

Так как операции выбора компонентов структурированных объ­ектов используются со структурами и объединениями, то необходи­мые пояснения и примеры приведем позже, введя перечисленные понятия и, кроме того, аккуратно определив указатели.

Запятая в качестве операции (ранг 15)

Несколько выражений, разделенных запятыми «,», вычисляют­ся последовательно слева направо. В качестве результата сохраня­ются тип и значение самого правого выражения. Таким образом, операция «запятая» группирует вычисления слева направо. Тип и значение результата определяются самым правым из разделенных запятыми операндов (выражений). Значения всех левых операн­дов игнорируются. Например, если переменная x имеет тип int, то значением выражения (x=3, 3*x) будет 9, а переменная x примет значение 3.

Скобки в качестве операций

Круглые ( ) и квадратные [ ] скобки играют роль бинарных опе­раций (ранг 1) при вызове функций и индексировании элементов массивов. Для программиста, начинающего использовать язык Си, мысль о том, что скобки в ряде случаев являются бинарными опе­рациями, часто даже не приходит в голову. И это даже тогда, когда он практически в каждой программе обращается к функциям или применяет индексированные переменные. Итак, отметим, что скоб­ки могут служить бинарными операциями, особенности и возмож­ности которых достойны внимания.

Круглые скобки обязательны в обращении к функции:

имя_функции(список_аргументов),

где операндами служат имя_функции и список_аргументов. Резуль­тат вызова определяется (вычисляется) в теле функции, структуру которого задает ее определение.

В выражении

имя_массива[индекс]

операндами для операции [ ] служат имя_массива и индекс. Подроб­нее с индексированными переменными мы познакомимся на при­мерах в главе 2 и более подробно в следующих главах.

Тернарная (условная трехместная) операция (ранг 13). В от­личие от унарных и бинарных операций, тернарная операция ис­пользуется с тремя операндами. В изображении условной операции применяются два символа '?' и ':' и три выражения-операнда:

выражение_1 ? выражение_ 2 : выражение_3

Первым вычисляется значение выражения_1. Если оно истинно, то есть не равно нулю, то вычисляется значение выражения_2, кото­рое становится результатом. Если при вычислении выражения_1 по­лучится 0, то в качестве результата берется значение выражения_3. Классический пример:

x < 0 ? -x : x;

Выражение возвращает абсолютную величину переменной x.

Операция явного преобразования типа. Операция преобразова­ния (приведения) типа (ранг 2) имеет следующий формат:

(имя_типа) операнд

Такое выражение позволяет преобразовывать значение операнда к заданному типу. В качестве операнда используется унарное выра­жение, которое в простейшем случае может быть переменной, кон­стантой или любым выражением, заключенным в круглые скобки. Например, преобразования (long)8 (внутреннее представление ре­зультата имеет длину 4 байта) и (char)8 (внутреннее представление результата имеет длину 1 байт) изменяют длину внутреннего пред­ставления целых констант, не меняя их значений.

В этих преобразованиях константа не меняла значения и остава­лась целочисленной. Однако возможны более глубокие преобразо­вания, например (long double)6 или (float)4 не только изменяют длину константы, но и структуру ее внутреннего представления. В результатах будут выделены порядок и мантисса, значения будут вещественными.

Примеры:

long i = 12L;	/*	Определение переменной	*/
float brig;	/*	Определение переменной	*/
brig = (float)i;	/*	Явное приведение типа	*/

brig получает значение 12L, преобразованное к типу float.

Преобразования типов арифметических данных нужно приме­нять аккуратно, так как возможно изменение числовых значений. При преобразовании больших целочисленных констант к вещест­венному типу (например, к типу float) возможна потеря значащих цифр (потеря точности). Если вещественное значение преобразу­ется к целому, то возможна ошибка при выходе полученного зна­чения за диапазон допустимых значений для целых. В этом случае результат преобразования не всегда предсказуем и целиком зависит от реализации.

1.5. Разделители

Этот параграф может быть опущен при первом чтении, так как смысл почти всех разделителей становится очевиден при разборе той или иной конструкции языка. Однако полнота изложения сведе­ний о лексемах и их назначениях требует систематического рассмот­рения разделителей именно здесь, что мы и делаем. В дальнейшем этот раздел можно использовать для справок. В некоторых приме­рах данного параграфа пришлось использовать понятия, вводимые в следующих главах (например, структурный тип или прототип функции).

Разделители, или знаки пунктуации, входят в число лексем языка:

[ ] ( ) { } , ; : ... * = #

Квадратные скобки. Для ограничения индексов одно- и много­мерных массивов используются квадратные скобки [ ]. Примеры:

int A[5]; А - одномерный массив из пяти элементов;

int x, e[3][2]; e - двумерный массив (матрица) размером 3x2.

Круглые скобки. Назначение круглых скобок ( ):

1. 
   выделяют выражения-условия (в операторе «если»):
   

if (x < 0) x = -x;

/*абсолютная величина арифметической переменной*/

2. 
   входят как обязательные элементы в определение и описание (в прототип) любой функции, где выделяют соответственно список параметров и список спецификаций параметров:
   

float F(float x, int k) /* Определение функции*/

{ тело_функции }

float F(float, int); /* Описание функции - ее прототип */

3. 
   круглые скобки обязательны при определении указателя на функцию:
   

int (*pfunc)( ); /* Определение указателя pfuncна функцию */

4. 
   группируют выражения, изменяя естественную последователь­ность выполнения операций:
   

y = (a + b) / c; /* Изменение приоритета операций */

5. 
   входят как обязательные элементы в операторы циклов:
   

for (i=0, j=1; iтело_цикла;

while ( iтело_цикла;

do тело_цикла while ( k>0 );

6. 
   в макроопределениях настоятельно рекомендуется примене­ние круглых скобок, обрабатываемых препроцессором.
   

Фигурные скобки. Для обозначения соответственно начала и кон­ца составного оператора или блока используют фигурные скобки { }. Пример использования составного оператора в условном операторе:

if (d > x) { d--; x++; }

Пример блока - тело любой функции:

float absx (float x)

{

return x>0.0?x:-x;

}

Обратите внимание на отсутствие точки с запятой после закры­вающейся скобки '}', обозначающей конец составного оператора или блока.

Фигурные скобки используются для выделения списка компонен­тов в определениях структурных и объединяющих типов:

/* Определение структурного типа cell: */ struct cell

{

char *b;

int ee;

double U[6];

};

/* Определение объединяющего типа mix: */ union mix

{

unsigned int ii;

char cc[2];

};

Обратите внимание на необходимость точки с запятой после определения каждого типа.

Фигурные скобки используются при инициализации массивов и структур при их определении:

/* Инициализация массива: */

int month [ ] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 };

/* Инициализация структуры stock типа mixture */ struct mixture

{

int ii;

double dd;

char cc; }

stock = { 666, 3.67, '\t' };

В примере mixture - имя структурного типа с тремя компонента­ми разных типов, stock - имя конкретной структуры типа mixture. Компоненты ii, dd, cc структуры stock получают значения при ини­циализации из списка в фигурных скобках. (Подробно о структурах см. в главе 6.)

Запятая. Запятая может быть использована в качестве операции, а может применяться как разделитель. В последнем случае она раз­деляет элементы списков. Списками определяют начальные значе­ния элементов массивов и компонентов структур при их инициали­зации (примеры только что даны).

Другой пример списков - списки параметров аргументов в функ­циях.

Кроме того, запятая используется в качестве разделителя в за­головке оператора цикла:

for (x=p1,y=p2,i=2; i
(В данном примере после выполнения цикла значением перемен­ной z будет величина, равная n-му члену последовательности чисел Фибоначчи, определенной по значениям первых двух p1 и p2.)

Запятая как разделитель используется также в описаниях и опре­делениях объектов (например, переменных) одного типа:

int i, n;

float x, y, z, p1, p2;

Следует обратить внимание на необходимость с помощью круг­лых скобок отделять запятую-операцию от запятой-разделителя. Например, для элементов следующего массива m используется спи­сок с тремя начальными значениями:

int i=1, m[ ]={ i, (i=2,i*i), i };

В данном примере запятая в круглых скобках выступает в роли знака операции. Операция присваивания «=» имеет более высокий приоритет, чем операция «запятая». Поэтому вначале i получает значение 2, затем вычисляется произведение i*i, и этот результат служит значением выражения в скобках. Однако значением пере­менной i остается 2. Значениями m[0], m[1], m[2] будут соответ­ственно 1, 4, 2.

Точка с запятой. Каждый оператор, каждое определение и каждое описание в программе на языке Си завершает точка с запятой ';'. Любое допустимое выражение, за которым следует ';', воспринима­ется как оператор. Это справедливо и для пустого выражения, то есть отдельный символ «точка с запятой» считается пустым опера­тором. Пустой оператор иногда используется как тело цикла. При­мером может служить цикл for, приведенный выше для иллюстра­ции особенностей использования запятой в качестве разделителя. (Вычисляется n-й член последовательности чисел Фибоначчи.)

Примеры операторов-выражений:

i++; /* Результат - только изменение значения переменной i */

F(z,4); /* Результат определяется телом функции с именем F */

Двоеточие. Для отделения метки от помечаемого ею оператора используется двоеточие ':':

метка: оператор;

Многоточие. Это три точки '...' без пробелов между ними. Оно ис­пользуется для обозначения переменного числа аргументов у функ­ции при ее определении и описании (при задании ее прототипа). При работе на языке Си программист постоянно использует библиотеч­ные функции со списком аргументов переменной длины для формат­ных ввода и вывода. Их прототипы выглядят следующим образом:

int printf(char * format, ...);

int scanf (char * format, ...);

Здесь с помощью многоточия указана возможность при обраще­нии к функциям использовать разное количество аргументов (не меньше одного, так как аргумент, заменяющий параметр format, должен быть указан всегда и не может опускаться).

Подготовка своих функций с переменным количеством аргумен­тов на языке Си требует применения средств адресной арифмети­ки, например макросов, предоставляемых заголовочным файлом stdarg.h. О возможностях упомянутых макросов подробно говорит­ся в главе 5.

Звездочка. Как уже упоминалось, звездочка '*' используется в ка­честве знака операции умножения и знака операции разыменования (получения доступа через указатель). В описаниях и определениях звездочка означает, что описывается (определяется) указатель на значение использованного в объявлении типа:

/*Указатель на величину типа int*/ int * point;

/* Указатель на указатель на объект типа char */ char ** refer;

Обозначение присваивания. Как уже упоминалось, для обозна­чения операции присваивания используется символ '='. Кроме того, в определении объекта он используется при его инициализации:

/* инициализация структуры */

struct {char x, int y} A={ 'z', 1918 };

/* инициализация переменной */

int F = 66;

Признак препроцессорных директив. Символ '#' (знак номера или диеза в музыке) используется для обозначения директив (ко­манд) препроцессора. Если этот символ является первым отличным от пробела символом в строке программы, то строка воспринима­ется как директива препроцессора. Этот же символ используется в качестве одной из препроцессорных операций (см. главу 3).

Без одной из препроцессорных директив обойтись практически невозможно. Это директива

#include <stdio.h>

которая включает в текст программы средства связи с библиотеч­ными функциями ввода-вывода.

6. 
   Выражения
   

Введя константы, переменные, разделители и знаки операций, охарактеризовав основные типы данных и рассмотрев переменные, можно конструировать выражения. Каждое выражение состоит из одного или нескольких операндов, символов операций и ограничи­телей, в качестве которых чаще всего выступают круглые скобки ( ). Назначение любого выражения - формирование некоторого значе­ния. В зависимости от типа формируемых значений определяются типы выражений. Если значениями выражения являются целые и вещественные числа, то говорят об арифметических выражениях.

Арифметические выражения. В арифметических выражениях допустимы следующие операции:

• 
  + - сложение (или унарная операция +);
  
• 
  - - вычитание (или унарная операция изменения знака);
  
• 
  * - умножение;
  
• 
  / - деление;
  
• 
  % - деление по модулю (то есть получение остатка от цело­численного деления первого операнда на второй).
  

Операндами для перечисленных операций служат константы и переменные арифметические типы, а также выражения, заключен­ные в круглые скобки.

Примеры выражений с двумя операндами:

a+b 12.3-x 3.14159*Z k/3 16%i

Нужно быть аккуратным, применяя операцию деления '/' к цело­численным операндам. Например, как мы уже упоминали выше, за счет округления результата значением выражения 5/3 будет 1, а со­ответствует ли это замыслам программиста, зависит от смысла той конкретной конструкции, в которой это выражение используется.

Чтобы результат выполнения арифметической операции был ве­щественным, необходимо, чтобы вещественным был хотя бы один из операндов. Например, значением выражения 5.0/2 будет 2.5, что соответствует смыслу обычного деления.

Операции *, /, % (см. табл. 1.4) имеют один ранг (3), операции +, - также ранг (4), но более низкий. Арифметические операции одного ранга выполняются слева направо. Для изменения порядка выполнения операций обычным образом используются скобки. На­пример, выражение (d+b)/2.0 позволяет получить среднее арифме­тическое операндов d и b.

Как уже говорилось, введены специфические унарные операции ++ (инкремент) и — (декремент) для изменения на 1 операнда, ко­торый в простейшем случае должен быть переменной (леводопусти­мым значением). Каждая из этих операций может быть префиксной и постфиксной:

• 
  выражение ++m увеличивает на 1 значение m, и это получен­ное значение используется как значение выражения ++m (пре­фиксная форма);
  
• 
  выражение —k уменьшает на 1 значение k, и это новое значе­ние используется как значение выражения —k (префиксная форма);
  
• 
  выражение i++ (постфиксная форма) увеличивает на 1 значе­ние i, однако значением выражения i++ является предыдущее значение i (до его увеличения);
  
• 
  выражение j— (постфиксная форма) уменьшает на 1 значение j, однако значением выражения j— является предыдущее зна­чение j (до его уменьшения).
  

Например, если n равно 4, то при вычислении выражения n++*2 результат равен 8, а n примет значение 5. При n, равном 4, значением выражения ++n*2 будет 10, а n станет равно 5.

Внешнюю неоднозначность имеют выражения, в которых знак унарной операции ++ (или —) записан непосредственно рядом со знаком бинарной операции +:

x+++b или z d

В этих случаях трактовка выражений однозначна и полностью определяется рангами операций (бинарные аддитивные + и - имеют ранг 4; унарные ++ и — имеют ранг 2). Таким образом:

x+++b эквивалентно (x++)+b z d эквивалентно (z—)-d

Отношения и логические выражения. Отношение определяется как пара арифметических выражений, соединенных (разделенных) знаком операции отношения. Знаки операций отношения (уже были введены выше):

== равно; != не равно;


< меньше, чем;

> больше, чем;
<= меньше или равно;

>= больше или равно.

Примеры отношений:

a-b>6.3

(x-4)*3==12

6<=44

Логический тип в языке Си отсутствует, поэтому принято, что отношение имеет ненулевое значение (обычно 1), если оно истинно, и равно 0, если оно ложно. Таким образом, значением отношения 6<=44 будет 1.

Операции >, >=, <, <= имеют один ранг 6 (см. табл. 1.4). Операции сравнения на равенство = = и != также имеют одинаковый, но более низкий ранг 7, чем остальные операции отношений. Арифметиче­ские операции имеют более высокий ранг, чем операции отношений, поэтому в первом примере для выражения а-b не нужны скобки.

Логических операций в языке Си три:

• 
  ! - отрицание, то есть логическое НЕ (ранг 2);
  
• 
  && - конъюнкция, то есть логическое И (ранг 11);
  
• 
  || - дизъюнкция, то есть логическое ИЛИ (ранг 12).
  

Они перечислены по убыванию старшинства (ранга). Как прави­ло, логические операции применяются к отношениям. До выполне­ния логических операций вычисляются значения отношений, входя­щих в логическое выражение. Например, если a, b, c - переменные, соответствующие длинам сторон треугольника, то для них должно быть истинно, то есть не равно 0, следующее логическое выражение: a+b>c && a+c>b && b+c>a

Несколько операций одного ранга выполняются слева направо, причем вычисления прерываются, как только будет определена ис­тинность (или ложность) результата, то есть если в рассмотренном примере a+b окажется не больше c, то остальные отношения не рас­сматриваются - результат ложен.

Так как значением отношения является целое (0 или 1), то ничто не противоречит применению логических операций к целочислен­ным значениям. При этом принято, что любое ненулевое положи­тельное значение воспринимается как истинное, а ложной считает­ся только величина, равная нулю. Значением !5 будет 0, значением 4 && 2 будет 1 и т. д.

Присваивание. Как уже говорилось, символ «=» в языке Си обо­значает бинарную операцию, у которой в выражении должно быть два операнда - левый (модифицируемое именующее выражение - обычно переменная) и правый (обычно выражение). Если z - имя переменной, то

z = 2.3 + 5.1

есть выражение со значением 7.4. Одновременно это значение при­сваивается и переменной z. Только в том случае, когда в конце вы­ражения с операцией присваивания помещен символ «;», это выра­жение становится оператором присваивания. Таким образом,

z = 2.3 + 5.1;

есть оператор присваивания переменной z значения, равного 7.4.

Тип и значение выражения с операцией присваивания опреде­ляются значением выражения, помещенного справа от знака «=». Однако этот тип может не совпадать с типом переменной из левой части выражения. В этом случае при определении значения пере­менной выполняется преобразование (приведение) типов (о прави­лах приведения см. ниже в этом параграфе).

Так как выражение справа от знака «=» может содержать, в свою очередь, операцию присваивания, то в одном операторе присваива­ния можно присвоить значения нескольким переменным, то есть организовать «множественное» присваивание, например:

c = x = d = 4.0 + 2.4;

Здесь значение 6.4 присваивается переменной d, затем 6.4 как значение выражения с операцией присваивания «d=4.0+2.4» при­сваивается x и, наконец, 6.4 как значение выражения «x=d» присваи­вается c. Естественное ограничение - слева от знака «=» в каждой из операций присваивания может быть только леводопустимое вы­ражение (в первых главах книги - имя переменной).

В языке Си существует целый набор «составных операций при­сваивания» (ранг 14 в табл. 1.4). Как уже говорилось в §1.4, каждая из составных операций присваивания объединяет некоторую би­нарную логическую или арифметическую операцию и собственно присваивание. Операция составного присваивания может исполь­зоваться следующим образом:

имя_переменной ор=выражение;

где ор - одна из операций *, /, %, +, -, &, ^л, |, <<, >>. Если рас­сматривать конструкцию «ор=» как две операции, то вначале вы­полняется ор, а затем «=». Например:

x*=2; z+=4; i/=x+4*z;

При выполнении каждого из этих операторов операндами для операции ор служат переменная из левой части и выражение из правой. Результат присваивается переменной из левой части.

Таким образом, первый пример можно рассматривать как обозна­чение требования «удвоить значение переменной х»; второй при­мер - «увеличить на 4 значение переменной z»; третий пример - «уменьшить значение переменной i в (x+4*z) раз». Этим операторам эквивалентны такие операторы присваивания:

x=x*2; z=z+4; i=i/(x+4*z);

В последнем из них пришлось ввести скобки для получения пра­вильного результата. Обратите внимание на то, что использовать операции составного присваивания можно только в тех случаях, когда одна переменная используется в обеих частях. Более того, для некоторых операций эта переменная должна быть обязательно первым (левым) операндом. Например, не удастся заменить состав­ными следующие простые операторы присваивания:

a=b/a; x=z%x.

Приведение типов. Рассматривая операцию деления, мы отме­тили, что при делении двух целых операндов результат получается целым. Например, значением выражения 5/2 будет 2, а не 2.5. Для получения вещественного результата нужно выполнять деление не целых, а вещественных операндов, например, записав 5.0/2.0, полу­чим значение 2.5.

Если операндами являются безымянные константы, то заменить целую константу (как мы только что сделали) на вещественную со­всем не трудно. В том случае, когда операндом является именован­ная константа, переменная или выражение в скобках, необходимо для решения той же задачи использовать операцию явного приве­дения (преобразования) типа. Например, рассмотрим такой набор определений и операторов присваивания:

int n=5, k=2;

double d;

int m;

d=(double) n/ (double) k;

m=n/k;

В этом фрагменте значением d станет величина 2.5 типа double, а значением переменной m станет целое значение 2.

Операция деления является только одной из бинарных операций. Почти для каждой из них операнды могут иметь разные типы. Одна­ко не всегда программист должен в явном виде указывать преобра­зования типов. Если у бинарной операции операнды имеют разные типы (а должны в соответствии с синтаксисом выражения иметь один тип), то компилятор выполняет преобразование типов автома­тически, то есть приводит оба операнда к одному типу. Например, для тех же переменных значение выражения d+k будет иметь тип double за счет неявного преобразования, выполняемого автоматиче­ски без указания программиста. Рассмотрим правила, по которым такие приведения выполняются.

Правила преобразования типов. При вычислении выражений не­которые операции требуют, чтобы операнды имели соответствую­щий тип, а если требования к типу не выполнены, принудительно вызывают выполнение нужных преобразований. Та же ситуация возникает при инициализации, когда тип инициализирующего вы­ражения приводится к типу определяемого объекта. Напомним, что в языке Си присваивание является бинарной операцией, поэтому сказанное относительно преобразования типов относится и ко всем формам присваивания, однако при присваиваниях значение выра­жения из правой части всегда приводится к типу переменной из левой части, независимо от соотношения этих типов.

Правила преобразования в языке Си для основных типов опреде­лены стандартом языка. Эти стандартные преобразования включают перевод «низших» типов в «высшие».

Среди преобразований типов выделяют:

• 
  преобразования в арифметических выражениях;
  
• 
  преобразования при присваиваниях;
  
• 
  преобразования указателей.
  

Преобразование типов указателей будет рассмотрено в главе 4. Здесь рассмотрим преобразования типов при арифметических опе­рациях и особенности преобразований типов при присваиваниях.

При преобразовании типов нужно различать преобразования, изменяющие внутреннее представление данных, и преобразования, изменяющие только интерпретацию внутреннего представления. Например, когда данные типа unsigned int переводятся в тип int, менять их внутреннее представление не требуется - изменяется только интерпретация. При преобразовании значений типа double в значение типа int недостаточно изменить только интерпретацию, необходимо изменить длину участка памяти для внутреннего пред­ставления и кодировку. При таком преобразовании из double в int возможен выход за диапазон допустимых значений типа int, и реак­ция на эту ситуацию существенно зависит от конкретной реализа­ции. Именно поэтому для сохранения мобильности программ в них рекомендуется с осторожностью применять неявные преобразова­ния типов.

Рассмотрим последовательность выполнения преобразования операндов в арифметических выражениях.

1. 
   Все короткие целые типы преобразуются в типы не меньшей длины в соответствии с табл. 1.5. Затем оба значения, участ­вующие в операции, принимают одинаковый тип в соответ­ствии со следующими ниже правилами.
   
2. 
   Если один из операндов имеет тип long double, то второй тоже будет преобразован в long double.
   
3. 
   Если п. 2 не выполняется и один из операндов есть double, другой приводится к типу double.
   
4. 
   Если пп. 2-3 не выполняются и один из операндов имеет тип float, то второй приводится к типу float.
   
5. 
   Если пп. 2-4 не выполняются (оба операнда целые) и один операнд unsigned long int, то оба операнда преобразуются к типу unsigned long int.
   
6. 
   Если пп. 2-5 не выполняются и один операнд есть long, другой преобразуется к типу long.
   
7. 
   Если пп. 2-6 не выполняются и один операнд unsigned, то другой преобразуется к типу unsigned.
   
8. 
   Если пп. 2-7 не выполнены, то оба операнда принадлежат ти­пу int.
   

Таблица 1.5. Правила стандартных арифметических преобразований

Исходный тип	Преобразованный тип	Правила преобразований
char	int	Расширение нулем или знаком в зависимости от умолчания для char
unsigned char	int	Старший байт заполняется нулем
signed char	int	Расширение знаком
short	int	Сохраняется то же значение
unsigned short	unsigned int	Сохраняется то же значение
enum	int	Сохраняется то же значение
Битовое поле	int	Сохраняется то же значение

Используя арифметические выражения, следует учитывать при­веденные правила и не попадать в «ловушки» преобразования ти­пов, так как некоторые из них приводят к потерям информации, а другие изменяют интерпретацию битового (внутреннего) пред­ставления данных.

На рис. 1.2 стрелками отмечены «безопасные» арифметические преобразования, гарантирующие сохранение точности и неизмен­ность численного значения.



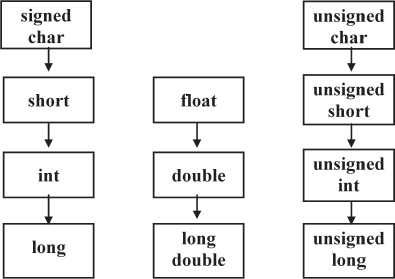
Рис. 1.2. Арифметические преобразования типов, гарантирующие сохранение значимости

При преобразованиях, которые не отнесены схемой (рис. 1.2) к безопасным, возможны существенные информационные потери. Для оценки значимости таких потерь рекомендуется проверить об­ратимость преобразования типов. Преобразование целочисленных значений в вещественные осуществляется настолько точно, насколь­ко это предусмотрено аппаратурой. Если конкретное целочисленное значение не может быть точно представлено как вещественное, то младшие значащие цифры теряются и обратимость невозможна.

Приведение вещественного значения к целому типу выполняется за счет отбрасывания дробной части. Преобразование целой величи­ны в вещественную также может привести к потере точности.

Операция поразрядного отрицания (дополнения или инвер­тирования битов) обозначается символом «

» и является унарной (одноместной), то есть действует на один операнд, который должен быть целого типа. Значение операнда в виде внутреннего битово­го представления обрабатывается таким образом, что формируется значение той же длины (того же типа), что и операнд. В битовом представлении результата содержатся 1 во всех разрядах, где у опе­ранда 0, и 0 в тех разрядах, где у операнда 1. Например:

unsigned char E='\0301', F;

F=E;

Значением F будет восьмеричный код '\076' символа '>' (см. при­ложение 1). Действительно, битовые представления значений E и F можно изобразить так:

11000001 - для значения переменной Е, то есть для '\0301';

00111110 - для значения переменной F, то есть для '\076'.

За исключением дополнения, все остальные поразрядные опера­ции бинарные (двухместные).

Операции сдвигов >> (вправо) и << (влево) должны иметь цело­численные операнды. Над битовым представлением значения левого операнда выполняется действие - сдвиг. Правый операнд определя­ет величину поразрядного сдвига. Например:

5<<2 будет равно 20;

5>>2 будет равно 1.

Битовые представления тех же операций сдвига можно изобра­зить так:

101<<2 равно 10100, то есть 20;

101>>2 равно 001, то есть 1.

При сдвиге влево на N позиций двоичное представление левого операнда сдвигается, а освобождающиеся слева разряды заполня­ются нулями. Такой сдвиг эквивалентен умножению значения опе­ранда на 2^N.


К автору: во сколько раз?
Сдвиг вправо на N позиций несколько сложнее. Тут следует от­метить две особенности. Первое - это исчезновение младших раз­рядов, выходящих за разрядную сетку. Вторая особенность - отсут­ствие стандарта на правило заполнения освобождающихся левых разрядов. В стандарте языка сказано, что когда левый операнд есть целое значение с отрицательным знаком, то при сдвиге вправо за­полнение освобождающихся левых разрядов определяется реали­зацией. Здесь возможны два варианта: освобождающиеся разряды заполняются значениями знакового разряда (арифметический сдвиг вправо) или освобождающиеся слева разряды заполняются нулями (логический сдвиг вправо).

При положительном левом операнде сдвиг вправо на N позиций эквивалентен уменьшению значения левого операнда в раз с отбра­сыванием дробной части результата. (Поэтому 5>>2 равно 1.)

Операция «поразрядное исключающее ИЛИ». Эта операция имеет очень интересные возможности. Она применима к целым операндам. Результат формируется при поразрядной обработке би­товых кодов операндов. В тех разрядах, где оба операнда имеют одинаковые двоичные значения (1 и 1 или 0 и 0), результат прини­мает значение 1. В тех разрядах, где биты операндов не совпадают, результат равен 0. Пример использования:

char a='A'; /* внутренний код 01000001 */

char z='Z'; /* внутренний код 01011010 */

a=az; /* результат: 11100100 */

z=az; /* результат: 01000001 */

a=az; /* результат: 01011010 */

Переменные a и z «обменялись» значениями без использования вспомогательной переменной!

Поразрядная дизъюнкция (поразрядное ИЛИ) применима к це­лочисленным операндам. В соответствии с названием она позволяет получить 1 в тех разрядах результата, где не одновременно равны 0 биты обоих операндов. Например:

5 | 6 равно 7 (для 5 - код 101, для 6 - код 110);

10 | 8 равно 10 (для 10 - код 1010, для 8 - код 1000).

Поразрядная конъюнкция (поразрядное И) применима к цело­численным операндам. В битовом представлении результата только те биты равны 1, которым соответствуют единичные биты обоих операндов. Примеры:

5&6 равно 4 (для 5 - код 101, для 6 - код 110);

10&8 равно 8 (для 10 - код 1010, для 8 - код 1000).

Условное выражение. Как уже говорилось в §1.4, операция, вво­димая двумя лексемами '?' и ':' (она имеет ранг 13), является уни­кальной. Во-первых, в нее входит не одна, а две лексемы, во-вторых, она трехместная, то есть должна иметь три операнда. С ее помощью формируется условное выражение, имеющее такой вид:

операнд_1 ? операнд_2 : операнд_3

Все три операнда - выражения. Операнд_1 - это арифметическое выражение и чаще всего отношение либо логическое выражение. Ти­пы операнда_2 и операнда_3 могут быть разными (но они должны быть одного типа или должны автоматически приводиться к одному типу).

Первый операнд является условием, в зависимости от которого вычисляется значение выражения в целом. Если значение перво­го операнда отлично от нуля (условие истинно), то вычисляется значение операнда_2, и оно становится результатом. Если значение первого операнда равно 0 (то есть условие ложно), то вычисляется значение операнда_3, и оно становится результатом.

Примеры применения условного выражения мы уже приводили в §1.4.

Контрольные вопросы

1. 
   Какие типы данных приняты в языке и как они определяются (описываются)?
   
2. 
   Какие операции над данными допустимы в языке, как строятся с их помощью выражения и как они выполняются?
   
3. 
   Дайте определение служебного слова.
   
4. 
   Как используются служебные слова для обозначения типов дан­ных?
   
5. 
   Перечислите типы констант.
   
6. 
   Какой тип имеет целочисленная константа без суффикса?
   
7. 
   Совпадают ли коды символов '\0' и '0'?
   
8. 
   Перечислите суффиксы, определяющие тип целой константы.
   

9. 
   Перечислите суффиксы, определяющие тип вещественной кон­станты.
   
10. 
    Объясните назначения эскейп-последовательностей.
    
11. 
    Чем различаются знаковые и беззнаковые целые?
    
12. 
    Каковы размеры участков памяти, выделяемых для представле­ния арифметических констант?
    
13. 
    Из каких частей состоит вещественная константа?
    
14. 
    Как в языке Си определяется понятие объекта?
    
15. 
    Что такое «переменная»?
    
16. 
    Приведите форму определения переменных.
    
17. 
    Перечислите арифметические операции в порядке возрастания их рангов.
    
18. 
    Объясните различия между префиксной и постфиксной форма­ми операций декремента и инкремента.
    
19. 
    Объясните возможности применения запятой в качестве опера­ции.
    
20. 
    Приведите примеры использования поразрядных операций и операций сдвигов.
    
21. 
    Знаки каких бинарных операций могут использоваться в состав­ных операциях присваивания?
    
22. 
    Какого типа должны быть операнды тернарной (условной) опе­рации?
    
23. 
    К каким операндам применимы операции ++ и —?
    
24. 
    В чем особенность деления целочисленных операндов?
    
25. 
    Назовите правила выполнения операции %.
    
26. 
    Перечислите арифметические преобразования, гарантирующие сохранение значимости.